Sine and Cosine Rule: Comprehensive Guide with Worksheet
Sine and Cosine Rule
- The learning of triangles is one of the main parts of the geometry course; generally, you solve problems where you are asked either to find the lengths of its sides or the angles.
- Sine and Cosine Rules are two formulas that can be used for solving such problems and side being an advantage when dealing with non-right angled triangles.
In this article, we will discuss:
- What is the Sine and Cosine Rule?
- Steps for finding the Side of a Triangle using the Sine and Cosine Rule
- Steps for finding the Area of a Triangle using the Sine and Cosine Rule
Here is one more link to practice a few extra questions: Maths Genie Sine and Cosine Rule Questions
What is Sine Rule?
- As per the Sine Rule, the ratio of the length of a side of a triangle to the sine of the vertex opposite to that side is the same for all 3 sides of the triangle.
- In other words, for a triangle ABC, we have:
Where a, b, and c specify the lengths of the sides of the triangle, and A, B, and C denote the angles opposite the given sides.
Steps for finding the Side of a Triangle using Sine Rule
- Step #1: Identify the angle and the corresponding side of the triangle that you are required to determine the length of.
- Step #2: Write down the Sine Rule formula, which is
- Step #3: Substitute those already known values that are presented by other angle and its opposite side into the formula.
- Step #4: We rewrite the formula with the unknown side being the subject.
- Step #5: Put in the values and solve the equation for the unknown side.
Solved Example:
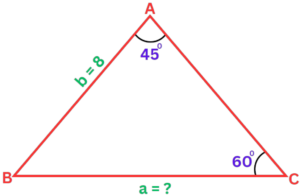
Question: Consider for example a triangle with sides A, B and C and angles A, B, and C, where side b is 8 units long and its angles A and B are 45 and 60 degrees, correspondingly. We want to find the length of side a.
Solution:
- Step #1: Determine which side of the triangle is the angle and opposite side you need to calculate the length. In this case, we are looking for side a, which is the side opposite angle A.
- Step #2: Write down the Sine Rule formula, which is
- Step #3: Insert the values of the other angle and its opposite side for the known ones in the formula.
Since angle B is 60 degrees and side “b” is of 8 units
a / sin 45 = 8 / sin 60
- Step #4: Rearrange the formula so that the unknown side becomes the subject.
We can rearrange the formula to isolate side a:
a = 8 x sin 45 / sin (60)
- Step #5: Replace the known sides with the values and solve for the unknown side.
We can simplify the denominator of the sine function to get:
a = 8 x sin 45 / sin 60
a = 6.53 units
Thus, side a has the length of 6. 53 units.
Practice Questions
Question 1: Suppose we have a triangle with sides x, y and z angles A, B, and C, where angle A is 30 degrees, angle B is 45 degrees, and side y is 10 units long. Determine the length of side x.
Answer :Question 2: Consider a triangle with sides a, b and c and angles A, B and C. If angle A is 75 degrees, angle C is 40 degrees and side b is 12 units long, find the length of side a.
Answer :Steps for finding the Angle of a Triangle using Sine Rule
- Step #1: The side and the opposite angle of the triangle for which the measure is to be found need to be identified.
- Step #2: Write down the Sine Rule formula, which is
- Step #3: Replace the known values of the other side and its opposite angle in the formula.
- Step #4: Rearrange the formula so that now you have the unknown angle as the subject.
- Step #5: Replace the values and solve for the unknown side.
What is Cosine Rule?
- The Cosine Rule on the other hand is a formula that when given the two sides of a triangle and the angle that is between the two sides, it can be used to determine the length of any of the sides of the right triangle.
- The formula is:
a2 = b2 + c2 – 2bc cos A
Where, a, b and c are the sides of the triangle, and A is the angle between the side b and c.
- The Cosine Rule can also be used to find the angle of a triangle if all three sides are known:
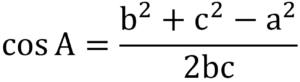
- Where a, b and c, are the side lengths of the triangle and A is the angle of the triangle formed by sides b and c.
Steps for finding the Side of a Triangle using Cosine Rule
- Step #1: Determine which side measurement for the triangle is unknown or is required to be determined.
- Step #2: State the Cosine Rule formula, which is illustrated as a² = b² + c² – 2bc cos A.
- Step #3: Replace the values of the two other sides and the angle between them into the formula.
- Step #4: This is also the simplified form of the equation, but if any arithmetic operations need to be performed, then they should be done now.
- Step #5: Then we isolate the unknown side by taking the square root of both sides of the equation.
- Step #6: Replace the values and solve for the unknown side.
Solved Example:
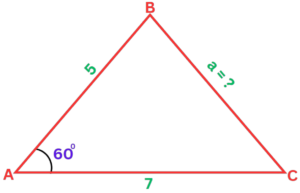
Question: Find the length of the side “a” in a triangle with sides of lengths 5 and 7, and an included angle of 60 degrees.
Solution:
- Step #1: Identify the side “a” as the one to be found.
- Step #2: Write the formula as
a² = b² + c² – 2bc cos A,
where a = unknown, b = 5, c = 7, and A = 60 degrees.
- Step #3: Substitute the known values into the formula:
a² = 5² + 7² – 2(5)(7)cos 60°.
- Step #4: Simplify the equation by performing the arithmetic operations:
a² = 25 + 49 – 70 cos 60°.
- Step #5: Take the square root of both sides to isolate the unknown side:
a = sqrt(25 + 49 – 70 cos 60°).
- Step #6: Substitute the value of cos 60° (which is 1/2) and solve for the unknown side:
a = sqrt(74 – 35) = sqrt(39) ≈ 6.25.
Therefore, the length of the unknown side “a” is approximately 6.25 units.
Practice Questions
Question 1: Determine the length of side b in a triangle with sides of lengths 8 and 10, and an included angle of 75 degrees.
Answer :Question 2: Find the length of side c in a triangle with sides of lengths 12 and 15, and an included angle of 40 degrees.
Answer :Steps for finding the Angle of a Triangle using Cosine Rule
- Step #1: Identify the angle of the triangle that you need to find the measure of.
- Step #2: Write down the Cosine Rule formula, which is
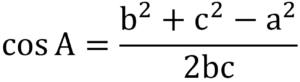
- Step #3: Substitute the known values of the three sides into the formula.
- Step #4: Rearrange the formula to make the unknown angle the subject.
- Step #5: Use a calculator to evaluate the inverse cosine function of the value obtained after rearranging the formula. This will give you the measure of the unknown angle.
- Step #6: Substitute the values and solve for the unknown angle.
Solved Example
Question: Find the measure of angle A in a triangle with sides of length 8, 10, and 12.
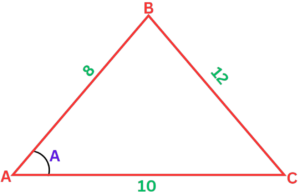
Solution:
- Step #1: Identify the angle A.
- Step #2: Write down the Cosine Rule formula, which is
cos A = (b² + c² – a²) / 2bc
- Step #3: Substitute the values of a, b, and c into the formula, we get:
cos A = (8² + 10² – 12²)/2(8)(10)
- Step #4: Rearrange the formula to make the unknown angle the subject:
cos A = (64 + 100 – 144) / (2 x 8 x 10)
cos A = 0.025
- Step #5: Use a calculator to evaluate the inverse cosine function of 0.025, which gives:
A = cos-1(0.125) = 82.82 degrees
Therefore, the measure of angle A in the triangle is approximately 82.82 degrees.
Area of a Triangle
- Finding the area of a triangle can be done using a variety of methods, including the Sine Rule.
- The Sine Rule is a useful formula for solving triangles, as it relates the ratios of the sides to the sines of their opposite angles.
Steps for finding the Area of a Triangle using Sine Rule
To find the area of a triangle using the Sine Rule, follow these steps:
- Step #1: Identify the two sides and the angle between them that you need to use in the formula.
- Step #2: Use the Sine Rule formula for the area of a triangle, which is
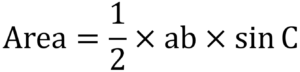
where a and b are the two sides and C is the angle between them.
- Step #3: Substitute the known values of a, b, and C into the formula.
- Step #4: Simplify the equation by performing any necessary arithmetic operations.
- Step #5: Calculate the value of sin C using a calculator.
- Step #6: Substitute the values into the formula and solve for the area.
Solved Example
Question: Consider a triangle with sides of length 5 and 7 and an angle of 60 degrees between them.
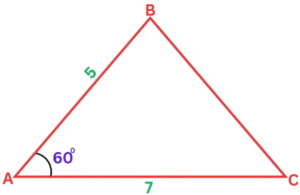
Solution:
- Step #1: Utilize the formula for the area of a triangle using the Sine Rule
A = 1/2 x ab x sin C.
- Step #2: Substitute the given values into the formula, where a and b are the lengths of the sides, and C is the angle between them.
A = 1/2 x 5 x 7 x sin 60,
- Step #3: Simplify the expression.
A = 15.16
Therefore, the area of the triangle is approximately 15.16 square units.
Practice Questions
Question 1: Consider a triangle with sides of length 12 and 15 and an angle of 30 degrees between them. Determine the area of the triangle by applying the Sine Rule.
Answer :Question 2: In a triangle with sides of lengths 6 and 8 and an included angle of 75 degrees, calculate the area using the Sine Rule.
Answer :Conclusion
- The sine and cosine rule are indispensable tools in trigonometry, offering versatile applications in solving triangles with varying configurations.
- These rules provide effective means for determining side lengths and angles in triangles, particularly when information about one angle and its corresponding sides is known.
- the sine and cosine rule significantly contribute to the toolkit of mathematical methods, offering solutions to a wide range of geometric problems involving triangles with different characteristics.
- The sine and cosine rule complement each other, providing alternative approaches to solving triangles based on the information available.
Worksheet on Sine and Cosine Rule
Question 1: In triangle ABC the length of AC is 15cm. Angle ABC = 112° Angle BAC = 33° Work out the length of BC.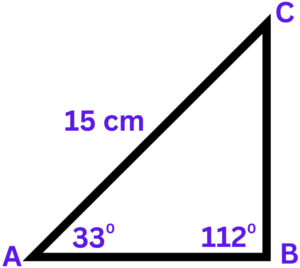 
Question 2: Calculate the area of the triangle.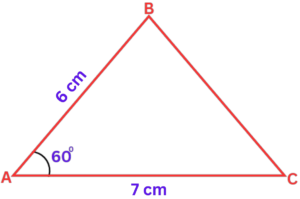 
Question 3: Calculate the size of angle ABC.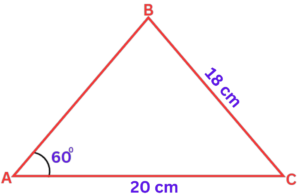 
Question 4: Calculate the size of the angle labelled y. 