Equation of a line: Graphs, Examples With Worksheet

Equation of a line

Linear equations are a prominent part of algebra. It represents a relationship between two variables represented in a straight-line form.
A line equation is a basic notion that is common in different fields which include physics, engineering, economics, and data science among others.

In this article, we will discuss:

What is the Equation of a Line?
How to Find the Equation of a Line

Here is one more link to practice a few extra questions: Maths Genie Equation of a Line Questions

What is the Equation of a Line?

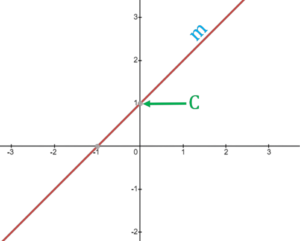
In mathematical terms, the equation for a line shows where the line is located in the Cartesian coordinate plane.
It is expressed as

y = mx + c,

where m is the gradient and c is the y-intercept.

In this example, m indicates line slope, and c shows y-intercept, which means where the line crosses the y-axis.
In case any (x, y) coordinate is on the line y = mx + c, x and y will be straightforwardly related linearly.
The term “linear equation” is given to equations that define straight lines.

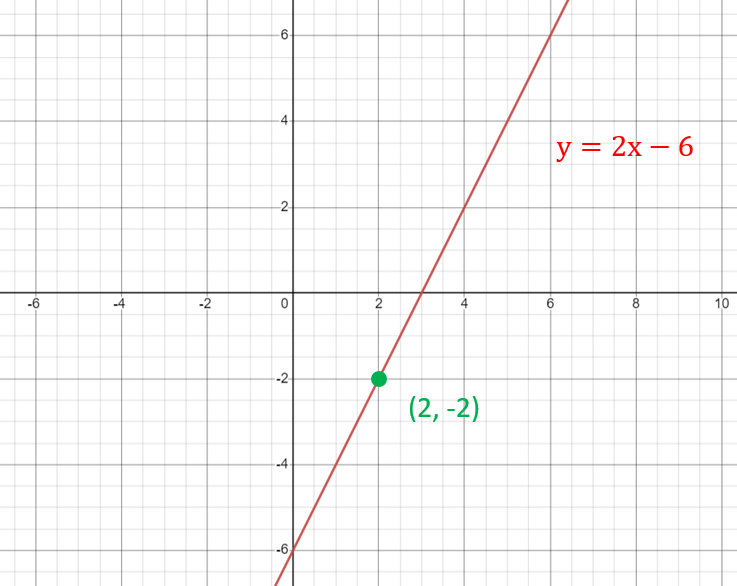
Solved Example:

Question 1: How would we get the y value for a given x in the line equation y= 2x – 6?

Solution:

Step #1: Analysis y = 2x -6.

Step #2: We can find any y-coordinate by inserting a designated x-value into the factored equation, say, x = 2

Step #3: Evaluate the required computations by selecting the x-value and finding the prescribed y-coordinate.

If x = 2

y = 2 x 2 – 6

y = 4 – 6

y = -2

Therefore, y equals -2 for the x value which is 2.

Practice Questions

Question 1. How can we find any y-coordinate for a given x value in the line equation y = 3x - 4?

Answer : ( , )

Question 2: How can we find any y-coordinate for a given x value in the line equation y = 5x - 3?

Answer : ( , )

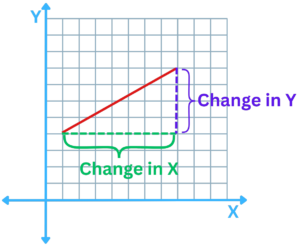
How do you find "m" and "c"?

c is easy: see at what point the line crosses the Y-axis.
m (the Slope) needs some calculation:

m = Change in Y/ Change in X

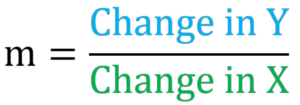
How to Find the Equation of a Line

Slope-Intercept Form (y = mx + b):

Work out two parameters (slope and y-intercept) from the information provided, e.g. a point on the line or the slope and a point.
Plug these values into the slope-intercept form to yield the equation.

Point-Slope Form (y – y₁ = m(x – x₁)):

If you are given the coordinates of a point (x₂, y₂) on the line along with its slope, you can use the point-slope form to write the equation for it.

Two-Point Form:

If you have two particular locations (x₁, y₁) and (x₂, y₂) on the line, then to acquire the equation, use the two-point form.

Parallel and Perpendicular Lines:

Note that lines with the same slope are parallel, while those with a negative reciprocal slope are perpendicular.
Make use of the given information to obtain the equation of a line parallel or perpendicular to a line.

Conclusion

The y = mx + c equation is extremely useful in not only representing but also depicting linear relationships, which is the reason why it is one of the pillars of algebra.
Among the various functions it has to fulfil the most significant is visualizing different phenomena, for example, the trajectory of the projectile or the trends in financial data.
Its versatility is not limited to a particular field of study and rather furnishes a way to comprehend and convey real-world cases.
The equation also provides geometrically the curve of slope and y-intercept which shows important information concerning the line’s relationship.

Worksheet

Question 1: A line has the equation y = 3x + 4. Write down the y-intercept of the line.

Question 2: Write down where these lines cross the y-axis (y-intercept): y = 2x + 3

Question 3: Find the coordinates where the following lines cross the x-axis: y = 2x + 6

Question 4: Find the coordinates where the following lines cross the x-axis: y = -2x + 10

Question 5: Write down where these lines cross the y-axis (y-intercept): y = 7x + 1