Parallel and Perpendicular Lines: Equations, Examples and Worksheet
Parallel and Perpendicular Lines
In the world of the mathematics and geometry, an idea of a line runs parallel with understanding the core concepts of mathematical knowledge.
Lines are a regular feature in the study of geometry, and they are mainly used to measure distances, creating shapes and solving equations.
In this article, we will discuss:
- What is a Gradient line of Parallel and Perpendicular Lines
- How to Find the Equation of Parallel and Perpendicular Lines
Here is one more link to practice a few extra questions: Maths Genie Parallel and Perpendicular lines Questions
General Equation of a Line
- The general equation of the line is critical in understanding the line’s behaviour.
- It can be expressed as
y = mx + c
or
ax + by + c = 0.
In the form ax + by + c = 0, the letters a and b are coefficients, and c is the intercept from the origin.
This form is indispensable for finding parallel and perpendicular lines.
Finding the Gradient of a Line
- The gradient (slope) is the one that governs the forming of a line’s equation.
- The formula for gradient:
(y2 – y1) / (x2 – x1), where (x1, y1) and (x2, y2)
are points on the line.
An equation y = mx + c has a gradient of m, where m is the coefficient of x.
Example: The line y = 2x + 3 has a slope of 2.
Solved Example: Gradient of a Line
Question 1: Find the gradient of the line passing through the points (3, 4) and (7, 10).
Solution:
Using the formula (y2 – y1) / (x2 – x1), we get:
(10 – 4) / (7 – 3) = 6 / 4
= 3 / 2
Therefore, the gradient of the line is 3/2.
Question 2: Find the gradient of the line with equation 4x – 2y = 8.
Solution:
Rearranging the equation into slope-intercept form, we get:
-2y = -4x + 8
y = 2x – 4
Therefore, the gradient of the line is 2.
Gradient of Parallel and Perpendicular Lines
The Gradient (slope) of Parallel Lines
The gradient of parallel lines does not change.
If two lines are parallel, then their slopes will be equal.
- For example, lines y = 2x + 5 and y = 2x – 1 have a gradient of 2.
As a consequence of this, the lines may be named as parallel ones.
- Parallel lines have equal slopes:
The Gradient (slope) of Perpendicular Lines:
The slope of perpendicular lines is a little bit different.
If two lines are perpendicular, their slopes will be the opposite reciprocals.
Therefore, in this case, if a line has a slope of m then, the other line of the equation will have a slope of -1/m.
To illustrate this, take a line with the equation y = 3x + 2. The perpendicular line will have a slope of -1/3. We get this by the negative reciprocal of 3.
- Thus, the equation of the perpendicular line will be y = (-1/3)x + b, where ‘b’ represents the y-intercept.
Solved Example: Gradient Formula for Parallel and Perpendicular Lines
Question 1: How can we determine if lines are parallel or perpendicular using the formula for finding the gradient between two points?
Solution:
- Step #1: Understanding Gradient Relationships
The formula for finding the slope between two points is a good tool for understanding the relationships between the lines.
- Step #2: Parallel Lines
When lines are parallel, they mean they are the same gradient. By this, the term of their slopes also is the same.
- Step #3: Perpendicular Lines
When it comes to perpendicular lines, their gradients are opposite reciprocals of one another. The negative reciprocal of one line’s slope is the slope of the other line.
- Step #4: Calculation Example
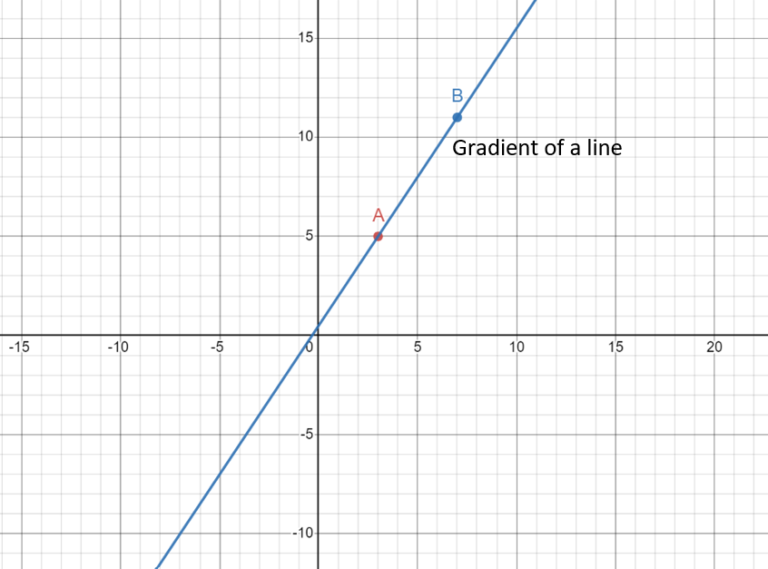
Let’s illustrate this with an example. Consider two points,
A(3, 5) and B(7, 11).
To calculate the gradient (slope) between these points, we use the formula:
Gradient = (change in y) / (change in x).
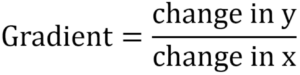
For A and B, this calculation is
(11 – 5) / (7 – 3) = 1.5.
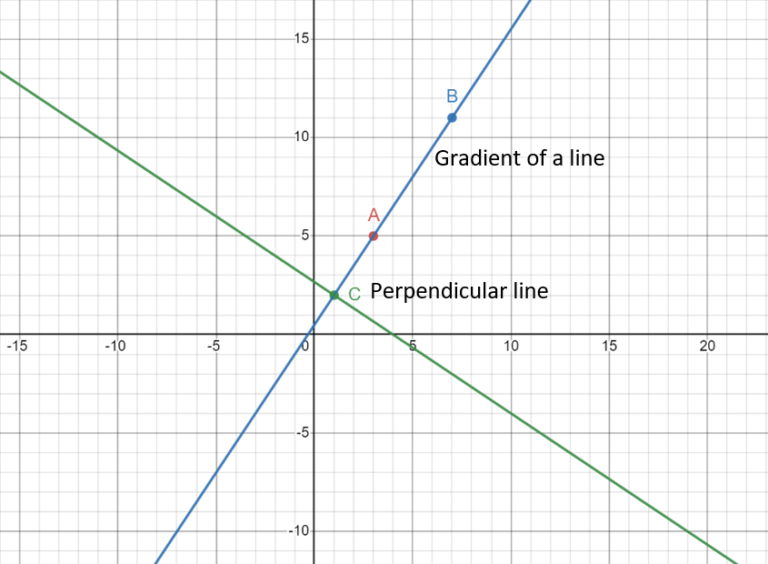
- Step #5: Introduce Another Point
Now, introduce another line with a point C(1, 2).
- Step #6: Determine the Relationship Using Gradients
Calculate the gradient of the line from point A to point C using the same equation. In this example, the slope between A and C is seen to be -2/3.
- Step #7: Identifying Parallel or Perpendicular Lines
If the gradient between points A and C is -2/3, it indicates that these lines are perpendicular. This determination arises from the fact that the gradient between A and B is 1.5, which is the negative reciprocal of -2/3.
- Step #8: Summary of Relationships
Summarizing, we can say that the same gradient is for parallel lines, and the gradients of perpendicular lines are the opposite of each other’s reciprocals. You can use the formula for the gradient of two points to decide quickly whether the lines are parallel or perpendicular.
Practice Questions
Question 1: Find the equation of the line parallel to y = 3x + 5 passing through the point (2, 1).
Answer :Question 2: Find the equation of the line perpendicular to y = -2x + 4 passing through the point (3, 5).
Answer :Finding the Equation of Parallel and Perpendicular Lines
- Finding an equation of a line that is parallel or perpendicular to the other line should be done only by taking some particular steps.
The process commences with the overview of the general equation of a line, y = mx + c; components within the equation consist of the dependent variable (y), independent variable (x), the coefficient of the slope (m) and the y-intercept (c).
Finding the Equation of a Parallel Line
- To find the equation of a parallel line, the following steps are essential:
Find out the slope of the given line.
Use the same slope to calculate the equation of the parallel line.
Decide on the y-intercept of the parallel line.
Solved Example
Question: How do you find the equation of a line that is parallel to y = 2x + 3 and passes through the point (5, 7)?
Solution:
To find the equation of a line that is parallel to y = 2x + 3 and passes through the point (5, 7), you can follow these steps:
- Step #1: Determine the Slope
The given line has a slope of 2. For a line parallel to it, the slope will also be 2.
- Step #2: Use the Slope-Intercept Form
The slope-intercept form of the equation of a line is y = mx + b, where ‘m’ is the slope, and ‘b’ is the y-intercept, which we need to find.
- Step #3: Substitute the Point
Since the parallel line passes through the point (5, 7), you can substitute these values into the equation to solve for ‘b’:
7 = 2(5) + b
- Step #4: Solve for ‘b’
Solving for ‘b’ in the equation, you get:
7 = 10 + b
Subtract 10 from both sides to isolate ‘b’:
b = 7 – 10
b = -3
- Step #5: Write the Equation
Now that you have found ‘b,’ you can write the equation of the parallel line:
y = 2x – 3
So, the equation of the line parallel to y = 2x + 3 and passing through the point (5, 7) is y = 2x – 3.
Practice Questions
Question 1: Find the equation of the line parallel to 2x - 3y = 7 and passing through the point (-1, 4).
Answer :Question 2: Find the equation of a line that is parallel to the line 3x + 2y = 8 and passes through the point (1, -3).
Answer :Finding the Equation of a Perpendicular Line
- To find the equation of a line that is perpendicular to another line, we need to follow these steps:
- Find out the gradient of the given line.
- Find the negative reciprocal of the slope to get the slope of the perpendicular line.
- Find the equation of the line passing through the point where the perpendicular one needs to be drawn.
Solved Example
Question: How do you find the equation of a line that is perpendicular to y = -3x + 2 and passes through the point (4, 1)?
Solution:
To find the equation of a line that is perpendicular to y = -3x + 2 and passes through the point (4, 1), you can follow these steps:
- Step #1: Determine the Slope
The given line has a slope of -3. For a line perpendicular to it, the slope will be the negative reciprocal, which is 1/3.
- Step #2: Use the Point-Slope Form
The point-slope form of the equation of a line is (y – y1) = m(x – x1), where ‘m’ is the slope, and (x1, y1) is a point on the line.
- Step #3: Substitute the Point
Since the perpendicular line passes through the point (4, 1), you can substitute these values into the point-slope form:
(y – 1) = (1/3)(x – 4).
- Step #4: Simplify the Equation
You can simplify the equation to get it in the slope-intercept form, which is y = mx + b:
(y – 1) = (1/3)(x – 4)
Distribute (1/3) to both terms in the parentheses:
y – 1 = (1/3)x – (4/3)
Now, add 1 to both sides to isolate ‘y’:
y = (1/3)x – (4/3) + 1
Simplify the constants:
y = (1/3)x – (4/3) + (3/3)
Combine the constants:
y = (1/3)x – (1/3)
So, the equation of the perpendicular line is y = (1/3)x – (1/3).
Practice Questions
Question 1: Find the equation of the line perpendicular to 4x + 3y = 12 and passing through the point (2, -1).
Answer :Question 2: Given the equation of a line as y = 3x + 2, find the equation of a line that is perpendicular to it and passes through the point (1, 5).
Answer :Conclusion
- To determine the equation of a line which is parallel to another one, we need to take the slope of the given line as the slope of the parallel line.
- Finding the slope of the line perpendicular to another line is done by finding the negative reciprocal of the slope of the line which is given.
- With the slope of the parallel or perpendicular line already available to us, we can use a single point on the line to find the y-intercept with the use of the point-slope form of the equation.
- Otherwise, we can make use of the direct point-slope form by providing the slope together with a point on the line to obtain the equation of this line.
- By doing so, we simply discovered the equation of a line which is either parallel or perpendicular to another line.
Worksheet on Parallel and Perpendicular Lines
Question 1: Find the equation of a line that is parallel to the line 2x - 3y = 6 and passes through the point (-1, 4).
Question 2: Find the equation of a line that is perpendicular to the line y = 4x - 1 and passes through the point (-2, 3).
Question 3: Find the equation of the line passing through the points (1, 2) and (-2, 5).
Question 4: Find the equation of a line that is perpendicular to the line 4x - 3y = 9 and passes through the point (2, 4).