3d Pythagoras Theorem: Examples with Worksheet
3d Pythagoras
- 3d Pythagoras theorem is a fundamental principle in geometry.
It enables us to calculate distances and measures in three-dimensional space.
In this article, we will discuss:
- What is 3D Pythagoras?
- 3D Pythagoras for Cuboids, Cones, Pyramids
- Using a 3D Pythagoras Theorem in calculating the total distance.
Here is one more link to practice a few extra questions: Maths Genie 3d Pythagoras Questions
What is 3D Pythagoras?
- The Pythagoras’ theorem is one of the basic (and central) theorems since it states about the connection between the sides of the right triangle.
- in two dimensions the Pythagorean theorem states that the square of the hypotenuse (longest side) added to the sum of squares of the other two sides is equal to the square of hypotenuse.
- But then, suppose the statement was true for a three-dimensional world. We can determine the stretch length between two points in terms of three dimensions using the Pythagoras theorem in the three-dimensional space. This implies the image from the same angle but presented in 3D.
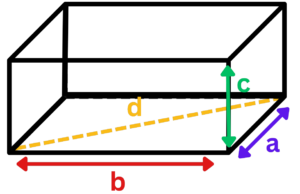
3D Pythagoras for Cuboids
- A cuboid is a three dimensional entity which has six faces each of rectangular shape. We employ 3D Pythagoras formula, to calculate the diagonal of the cuboid.
- Suppose we have a cuboid with sides of length a, b, and c. The diagonal d of the cuboid is given by:
d² = a² + b² + c²
Solved Example:
Question 1: Given a cuboid with sides a = 2cm, b = 3cm, and c = 4cm. What is the length of the diagonal?
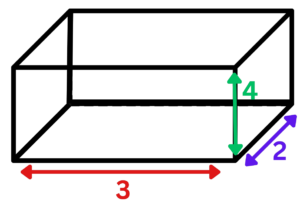
Solution:
- Step #1: If we want to showcase the 3D Pythagorean theorem, then it is a must that we completely understand its definition.
The formula for the diagonal (d) of a cuboid is given by the following: d2 = a2 + b2 + c2 and the formulas for a, b, c are the lengths of the cuboid’s sides.
- Step #2: Get rid of the side lengths
Employ the given sides’ lengths (a = 2 cm, b = 3 cm, c = 4 cm) in the stated formula.
d2 = 22 + 32 + 42 = 29
- Step #3: Find the Diagonal Length
Take the square root of the sum to find the diagonal length:
d = √29 ≈ 5.385 cm.
Therefore, the polygon having side 2 cm, 3 cm, and 4 cm is equivalent to approximately 5.385 cm and was derived by the employing 3 dimension Pythagorean rule.
Practice Questions
Question 1: Given a right triangular prism with a height of 8 units, a base length of 6 units, and a diagonal length of 10 units, find the length of the hypotenuse of the triangular face.
Answer :Question 2: Given a cuboid with sides of length 4 cm, 5 cm, and 7 cm, calculate the length of the main diagonal.
Answer :3D Pythagoras for Cones
- A cone is a three-dimensional shape that has a circular base and a vertex. We can use 3D Pythagoras to find the slant height of a cone.
- Suppose we have a cone with radius r and height h. The slant height s of the cone is given by:
s2 = r2 + h2
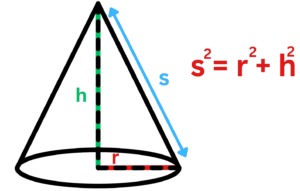
Solved Example:
Question 1: Keeping a right cone with 3 cm as its radius and 4 cm as its height in your mind, what is the slant height of the cone using Pythagoras’ theorem?
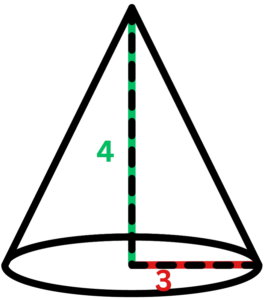
Solution:
- Step #1: Here is the equation of Pythagorean Theorem for the Cone.
The expression for the slant height (s) of a cone can be restated as s2 = r2 + h2, when r is the radius and h is the height.
- Step #2: Substitute Given Values
Substitute the given value (r = 2 cm, h = 4 cm) into the formula:
s2 = 32 + 42 = 25
- Step #3: Find the Slant Height
Take the square root of the sum to find the slant height:
s = √25 = 5 cm
Consequently, the slant length of the cone, being made up of a base of the radius 3 cm and the height of 4 cm, is 5 cm, calculated with the help of the Pythagorean Theorem.
Practice Questions
Question 1: A cone has a base radius of 4 units and a height of 7 units. Find the length of the slant height.
Answer :Question 2: A cone has a slant height of 15 cm and a height of h. If the radius is 9 cm, find the value of h using the Pythagorean Theorem.
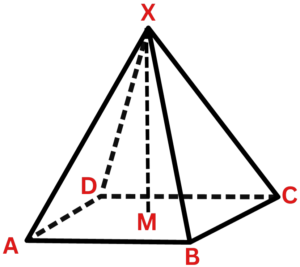
Answer :3D Pythagoras for Pyramids
- A pyramid is a three-dimensional shape that has a rectangular base and a vertex. We can use 3D Pythagoras to find the slant height of a pyramid.
- Suppose we have a pyramid with base edges of length a, and b, and height h. The slant heights of the pyramid is given by:
c2 = a2 + b2
s² = h² + (c/2)²
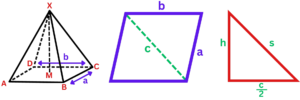
Solved Example:
Question 1: Given a pyramid with a rectangular base of length 3 cm, width 4 cm, and a height of 6 cm, how can we find the slant height of the pyramid using the Pythagorean Theorem?
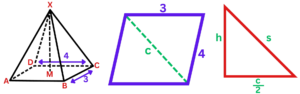
Solution:
- Step #1: Define the Pythagorean Theorem for the Pyramid
The formula for the slant height (s) of a pyramid with a rectangular base is given by s2 = c2 + h2, where c is half the diagonal of the base, and h is the height.
- Step #2: Calculate the Diagonal of the Base
Find half the diagonal of the base (c) using the Pythagorean Theorem for the rectangle:
c2 = 32 + 42 = 25
c = √25 = 5
- Step #3: Substitute Values into the Slant Height Formula
Substitute c = 5 and h = 6 into the slant height formula:
s2 = 62 + (5/2)2 = 48.5
- Step #4: Calculate the Slant Height:
Take the square root of the sum to find the slant height:
s ≈ √48.5 ≈ 6.96
Therefore, the slant height of the pyramid, with a rectangular base of length 3 cm and width 4 cm and a height of 6 cm, is approximately 6.96 cm, calculated using the Pythagorean Theorem.
Using 3D Pythagoras to Find Distance
- We can also use 3D Pythagoras to find the distance between two points in three-dimensional space.
- Suppose we have two points
P1(x1, y1, z1) and P2(x2, y2, z2).
- The distance between these two points d is given by:
d2 = (x2 – x1)2 + (y2 – y1)2 + (z2 – z1)²
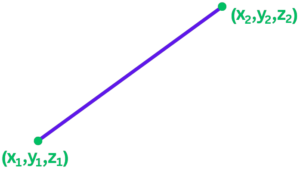
Solved Example:
Question 1: Consider two points in 3D space, P1(1, 2, 3) and P2(4, 5, 6). How can we calculate the distance between these two points using the 3D Pythagorean Theorem?
Solution:
- Step #1: Define the 3D Pythagorean Theorem
The formula for the distance (d) between two points in 3D space, P1(x1, y1, z1) and P2(x2, y2, z2), is given by
d2 = (x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2
- Step #2: Substitute Coordinates
Substitute the coordinates of the given points into the formula:
d2 = (4 – 1)2 + (5 – 2)2 + (6 – 3)2
= 27
- Step #3: Calculate the Distance
Take the square root of the sum to find the distance:
d ≈ √27 ≈ 5.196 cm
Therefore, the distance between the two points P1(1, 2, 3) and P2(4, 5, 6) in 3D space is approximately 5.196 cm, calculated using the 3D Pythagorean Theorem.
Practice Questions
Question 1: In a rectangular pyramid, the base measures 9 units by 12 units, and the height is 5 units. What is the length of the slant height?
Answer :Question 2: A square pyramid has a base side length of 8 units and a slant height of 10 units. Determine the height of the pyramid.
Answer :Exploring Further Concepts
The 3D Pythagoras concept has various applications in practical life, apart from basic geometry.
- Showings of architecture, engineering, and physics.
Drawing the connection between the everyday objects and the application of the 3D Pythagoras theorems.
Vector Analysis in regards to vector geometry applications.
Dispensing with vectors and their depiction through 3D space.
We are going to take 3D Pythagoras into vector operations.
Challenges and Advanced Applications
The latest skills in mastering 3D geometry problem-solving.
Advancing to difficult situations calling for an understanding of multiple fields of 3D Pythagoras.
- Strategies of taking on difficult issues in an organized manner.
Exploring interdisciplinary applications.
- Creating 3D Pythagoras and another concept in mathematics altogether.
- Analyzing its essence in the fields such as computer graphics design and robotics.
Conclusion
- 3D Pythagoras is a vital geometry discovery.
The cube makes it possible for us to count distances and measurements at three-dimensional space as well.
- Understanding 3D Pythagoras leads to a better comprehension of shapes and objects in our world.
Worksheet on 3d Pythagoras
Question 1: Find the radius of the cone with height 19 cm and slant length 23 cm. Give your answer correct to 1 decimal place.
Question 2: Here is a cuboid ABCDEFGH. Find the length AG. Give your answer correct to 1 decimal place.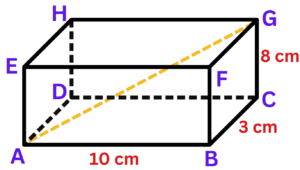
Question 3: Here is a cuboid ABCDEFGH. Find the length BH. Give your answer correct to 1 decimal place.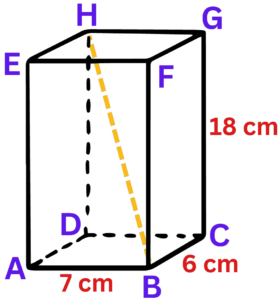
Question 4: The diagram shows a square-based pyramid ABCDX. AB = 40 cm,AX = BX = CX = DX = 50 cm. M is the centre of the square base ABCD. Calculate the length MX. Give your answer correct to 1 decimal place.
