Transformation of Graphs: A Comprehensive Guide with Worksheet

Calculator
Test Yourself

Transformation of Graphs

  • Graphs are an essential tool in studying functions and their behaviour.
  • Transforming the graph of a function involves changing its position or shape without changing the original function.
  • These transformations are achieved through various rules that apply to specific functions.

In this article, we will discuss:

  1. Horizontal Shift: f(x + a) and f(x – a)
  2. Vertical Shift: f(x) + a and f(x) – a
  3. Vertical Stretching/Shrinking: af(x) and 1/a f(x)
  4. Horizontal Stretching/Shrinking: f(ax) and f(x/a)
  5. Reflection: -f(x) and f(-x)

Here is one more link to practice a few extra questions: Maths Genie Transformation of Graphs Questions

Horizontal Shift: f(x + a) and f(x - a)

When we shift a graph horizontally, we move it left or right along the x-axis.

The function graph transformation rules for horizontal shifts are as follows:

  • f(x + a) shifts the graph of f(x) left by a units
  • f(x – a) shifts the graph of f(x) right by a units

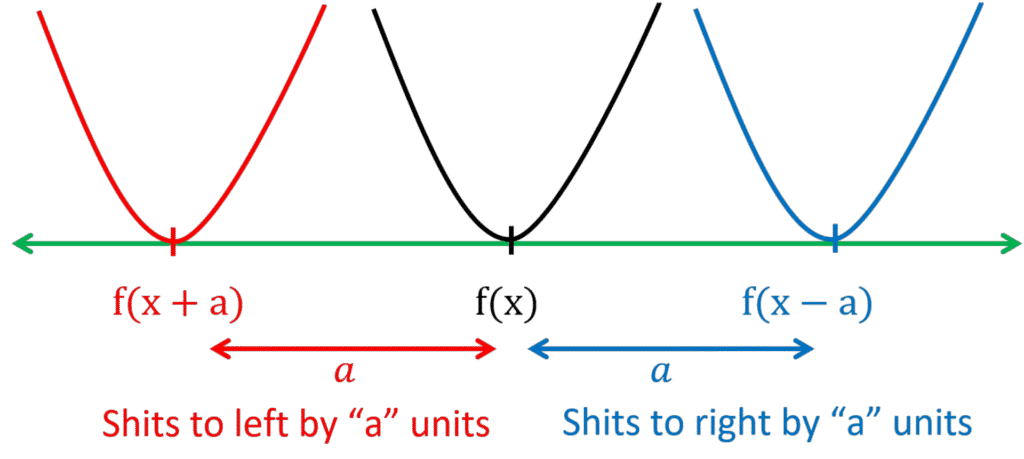
Graph showing horizontal shifts of the function f(x) with f(x + a) shifting left and f(x - a) shifting right.

certified Physics and Maths tutor

 

 

Solved Example: 

Consider the graph of the function f(x) = x².

If we apply the transformation rule f(x + 2), the new graph will shift two units to the left, resulting in the graph of the function f(x + 2) = (x + 2)².

Vertical Shift: f(x) + a and f(x) - a

  • A vertical shift moves the graph up or down along the y-axis.
The function graph transformation rules for vertical shifts are as follows:
  • f(x) + a vertically shifts the graph of f(x) upward by a units
  • f(x) – a vertically shifts the graph of f(x) downwards by a units
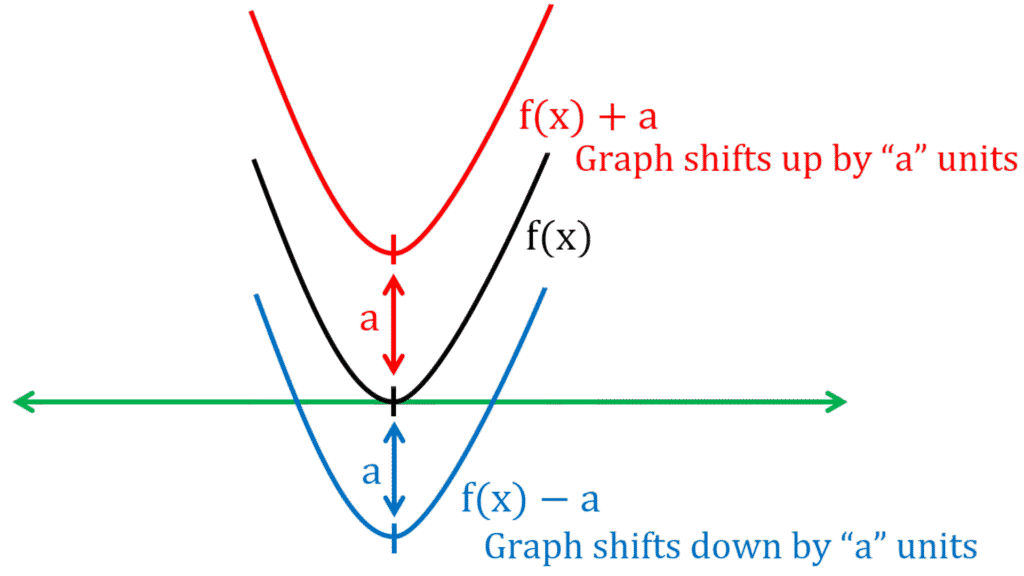
Graph showing vertical shifts of the function f(x) with f(x) + a shifting up and f(x) - a shifting down.
Request for Demo Lesson

certified Physics and Maths tutor

 

 

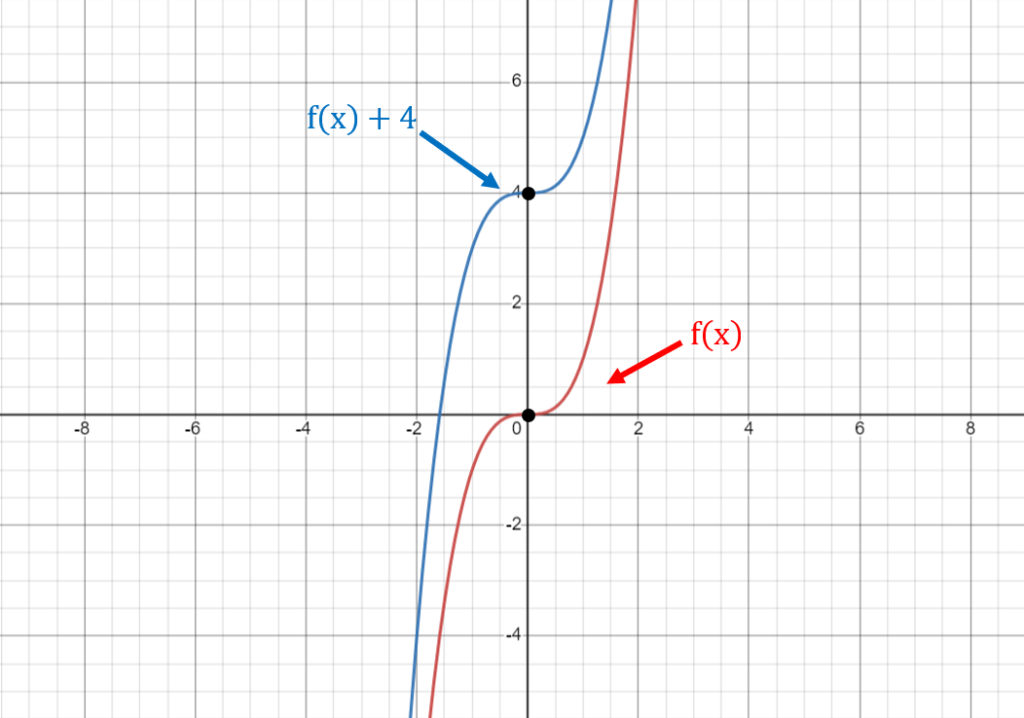
Solved Example: 

Let’s say we have the graph of the function f(x) = x³.

If we apply the transformation rule f(x) + 4, the new graph will shift four units up, resulting in the graph of the function f(x) + 4 = x³ + 4.

Vertical Shift f(x) + a and f(x) - a

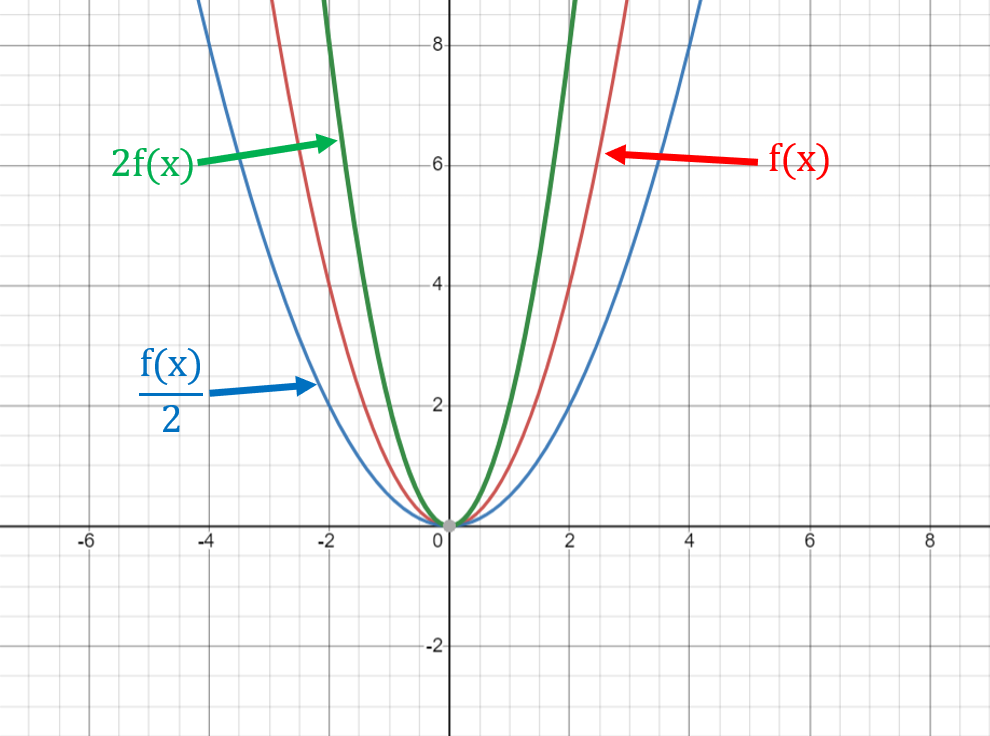
Vertical Stretching/Shrinking: af(x) and 1/a f(x)

Vertical stretching or shrinking of a graph changes the height of the graph.

The function graph transformation rules for vertical stretching/shrinking are as follows:

  • af(x) vertically stretches the graph of f(x) by a factor of a units
  • 1/a f(x) vertically shrinks the graph of f(x) by a factor of a units
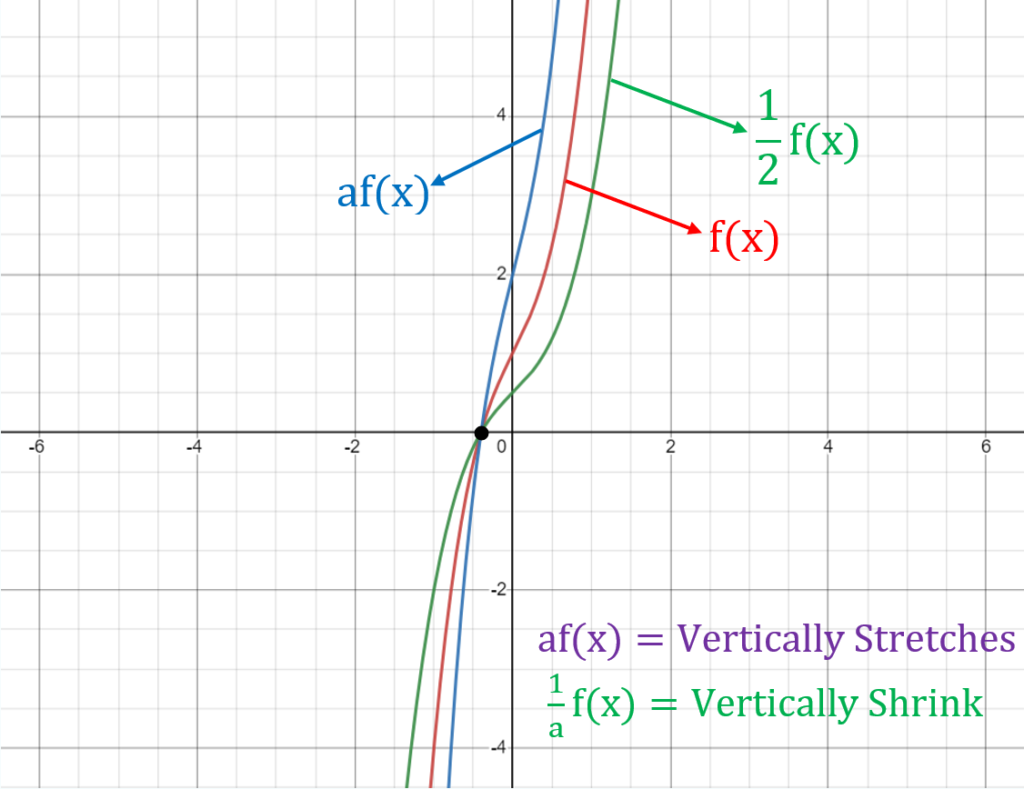
Transformation of Graphs vertically shrink

certified Physics and Maths tutor

 

 

Solved Example: Transformation of Graphs

Let’s consider the graph of the function f(x) = x².

If we apply the transformation rule 2f(x), the new graph will stretch vertically by a factor of 2, resulting in the graph of the function 2f(x) = 2x².

If we apply the transformation rule f(x)/2, the new graph will shrink vertically by a factor of 2, resulting in the graph of the function f(x)/2 = (1/2)x².

Transformation of Graphs Vertical Stretching and Shrinking

Horizontal Stretching/Shrinking: f(ax) and f(x/a)

Horizontal stretching or shrinking of a graph changes the width of the graph.

The function graph transformation rules for horizontal stretching/shrinking are as follows:

  • f(ax) horizontally shrinks the graph of f(x) by a factor of a units
  • f(x/a) horizontally stretches the graph of f(x) by a factor of a units
Transformation of Graphs vertically shrink

certified Physics and Maths tutor

 

 

Solved Example: Transformation of Graphs

Let’s say we have the graph of the function f(x) = cos(x).

If we apply the transformation rule f(2x), the new graph will shrink horizontally by a factor of 2, resulting in the graph of the function f(2x) = cos(2x).

If we apply the transformation rule f(x/2), the new graph will stretch horizontally by a factor of 2, resulting in the graph of the function f(x/2) = cos(x/2).

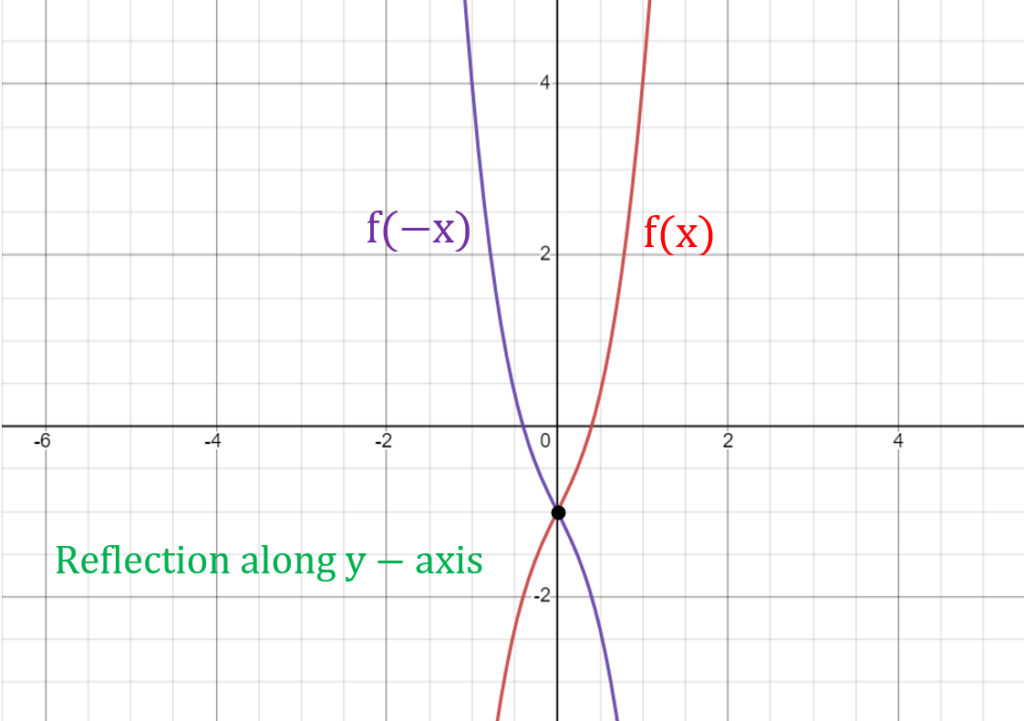
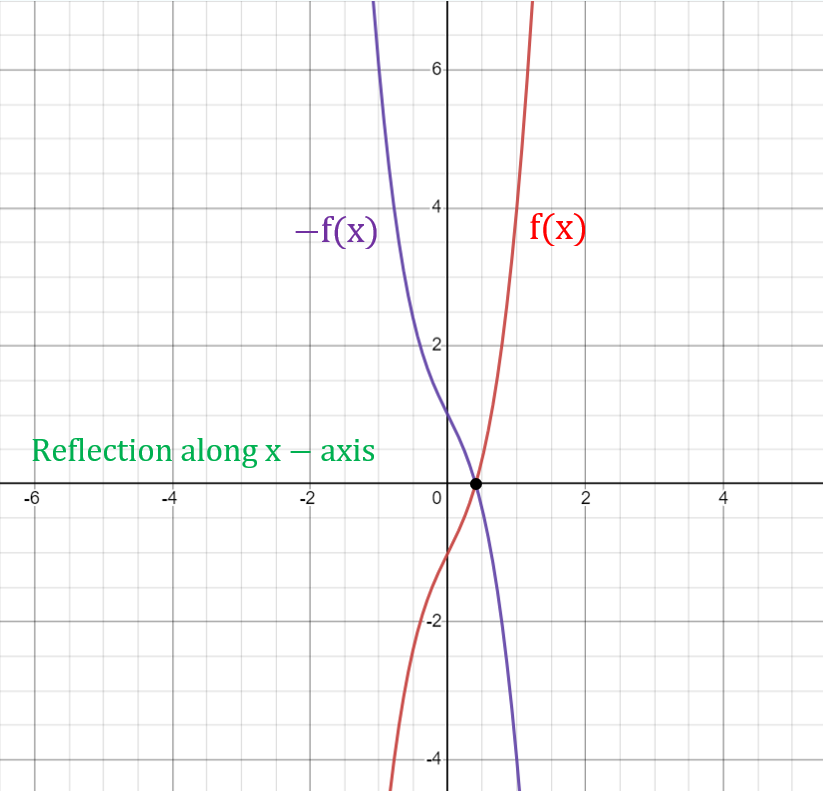
Reflection: -f(x) and f(-x)

Reflections of a graph involve flipping the graph across the x or y-axis.

The function graph transformation rules for reflections are:

  • Reflection across the x-axis: replace f(x) with -f(x) which reflects the graph of f(x) across the x-axis.
  • Reflection across the y-axis: replace x with -x in f(x) which reflects the graph of f(x) across the y-axis.
Transformation of Graphs Reflection on y- axis
Transformation of Graphs Reflection on x- axis

certified Physics and Maths tutor

 

 

Solved Example: Transformation of Graphs

Consider the function f(x) = x2. Here are some examples of its transformations:

  1. f(x + 2) shifts the graph left by 2 units.
  2. f(x – 3) shifts the graph right by 3 units.
  3. f(x) + 4 shifts the graph upwards by 4 units.
  4. f(x) – 1 shifts the graph downwards by 1 unit.
  5. 2f(x) vertically stretches the graph by a factor of 2.
  6. 1/3f(x) vertically shrinks the graph by a factor of 3.
  7. f(2x) horizontally shrinks the graph by a factor of 2.
  8. f(1/2x) horizontally stretches the graph by a factor of 2.
  9. -f(x) reflects the graph over the x-axis.
  10. f(-x) reflects the graph over the y-axis.
  • Note that you can apply multiple transformations to a single function.
  • For example, f(2x – 3) represents a horizontal shrink by a factor of 2 and a horizontal shift right by 3 units.

Conclusion

  • In conclusion, understanding the rules of function graph transformation is crucial for graphing and analysing functions.
  • You can easily recognize and apply these transformations to any given function with practice and understanding.

Practice Questions: Transformation of Graphs

Question 1: Consider the function f(x) = x2. Describe the transformation that occurs when f(x) is replaced by f(x + 3). Question 2: Consider the function g(x) = x3. Describe the transformation that occurs when g(x) is replaced by g(x – 2). Question 3: Describe the transformations necessary to transform the graph of f (x) into that of g(x).

f(x) = x3

g(x) = (x – 3)3 + 3

Question 4: Describe the transformations necessary to transform the graph of f (x) into that of g(x).

f(x) = x3

g(x) = (x + 1)3 + 2

Question 5: Describe the transformations necessary to transform the graph of f (x) into that of g(x).

f(x) = x2

g(x) = (x + 3)3 – 2

Question 6: Describe the transformations necessary to transform the graph of f (x) into that of g(x).

f(x) = x3

g(x) = -(x – 2)3

Question 7: Describe the transformations necessary to transform the graph of f (x) into that of g(x).

f(x) = x2

g(x) = (x + 1)2 – 3

Question 8: Describe the transformations necessary to transform the graph of f (x) into that of g(x).

f(x) = 1/x

g(x) = 3/x – 3

Question 9: Describe the transformations necessary to transform the graph of f (x) into that of g(x).

f(x) = x2

g(x) = -x2 + 2

Question 10: Transform the given function f (x) as described and write the resulting function as an equation

f(x) = x3

reflect across the x-axis

translate up 2 units

Solutions:

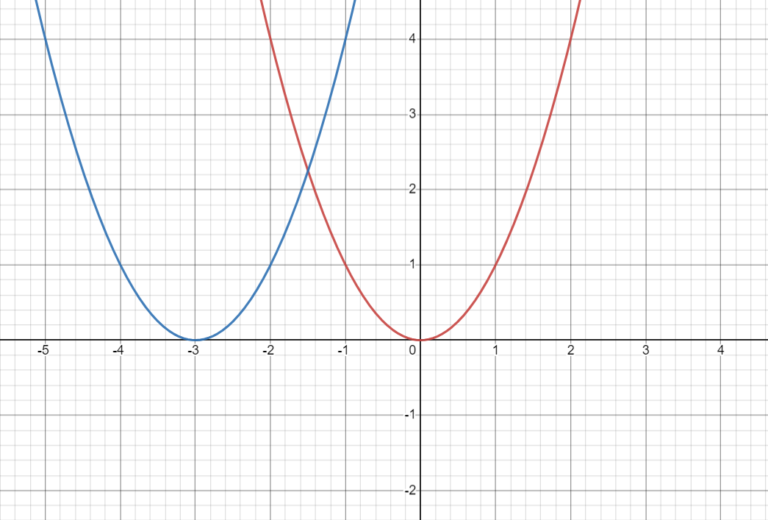
Question 1: Consider the function f(x) = x2. Describe the transformation that occurs when f(x) is replaced by f(x + 3).

Solution:

The transformation f(x + 3) represents a horizontal shift of the graph of f(x) to the left by 3 units.

Practice Question 1 Transformation of graph

Question 2: Consider the function g(x) = x3. Describe the transformation that occurs when g(x) is replaced by g(x – 2).

Solution:

The transformation f(x + 3) represents a horizontal shift of the graph of f(x) to the left by 3 units.

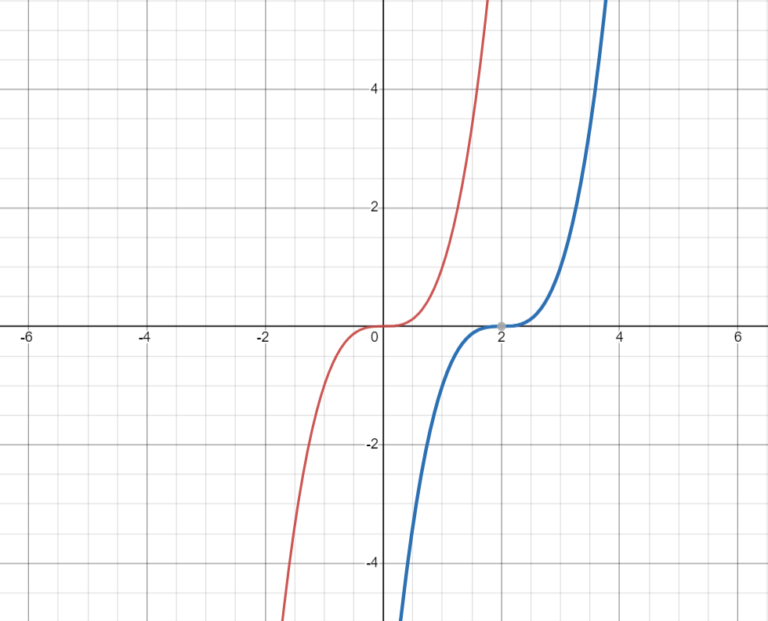
Practice Question 2 Transformation of graph
Question 3: Describe the transformations necessary to transform the graph of f (x) into that of g(x).

f(x)=x3

g(x)=(x-3)3+3

Solution:

translate right 3 units translate up 3 units

Question 4:Describe the transformations necessary to transform the graph of f (x) into that of g(x).

f(x)=x3

g(x)=(x+1)3+2

Solution:

translate left 1 unit translate up 2 units

Question 5:Describe the transformations necessary to transform the graph of f (x) into that of g(x).

f(x)=x2

g(x)=(x+3)3-2

Solution:

translate left 3 units translate down 2 units

Question 6:Describe the transformations necessary to transform the graph of f (x) into that of g(x).

f(x)=x3

g(x)=-(x-2)3

Solution:

reflect across the x-axis translate right 2 units

Question 7: Describe the transformations necessary to transform the graph of f (x) into that of g(x).

f(x)=x2

g(x)=(x+1)2-3

Solution:

translate left 1 unit translate down 3 units

Question 8:Describe the transformations necessary to transform the graph of f (x) into that of g(x).

f(x)=1/x

g(x)=3/x – 3

Solution:

expand vertically by a factor of 3 translate down 3 units

Question 9: Describe the transformations necessary to transform the graph of f (x) into that of g(x).

f(x)=x2

g(x)=-x2+2

Solution:

reflect across the x-axis translate up 2 units

Question 10:Transform the given function f (x) as described and write the resulting function as an equation

f(x)=x3

reflect across the x-axis

translate up 2 units

Solution:

g(x)=-x3 + 2