Quadratic Sequence: GCSE Questions, Examples with and Worksheet

Calculator
Test Yourself

Quadratic Sequence

  • Quadratic sequences represent a captivating area of mathematical study, offering a window into the enchanting world of patterns, equations, and numerical relationships.

  • These sequences, defined by their quadratic nature, are a cornerstone of algebra, serving as a crucial tool for modelling real-world phenomena and solving mathematical puzzles.

In this article, we will discuss: 

  1. What is a Quadratic Sequence?​
  2. The formula for Quadratic Sequence?
  3. Finding the nth term of a Quadratic Sequence?

Here is one more link to practice a few extra questions: Maths Genie Quadratic Sequence Questions

What is a Quadratic Sequence?​

  • Quadratic sequences are mathematical sequences where the difference between the terms is not constant.
  • In contrast to linear sequences, where the difference is constant, quadratic sequences have constant differences between the differences of their terms.
  • This means that the sequence of first differences is a linear sequence.
  • Let’s take an example to understand this better:

Sequence: 1, 4, 9, 16, 25, …

1st Differences: 3, 5, 7, 9, …

2nd Differences: 2, 2, 2, …

Quadratic Sequence Example

  • As we can see, the differences between the terms are not constant, but the differences between the first differences are constant. Therefore, we can conclude that this is a quadratic sequence.
Request for Demo Lesson

Practice Questions

Question 1: Find the next three terms in the quadratic sequence: 2, 6, 12, 20, ...

Answer :


Question 2: Find the next three terms in the quadratic sequence: 4, 13, 25, ...

Answer :

Formula for Quadratic Sequence

  • One can recognize and continue a quadratic sequence, and find the formula for the nth term of a quadratic sequence in terms of n.

  • The formula for the nth term of a quadratic sequence is in the form of

an = an2 + bn + c.

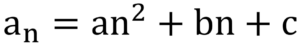
Quadratic Sequence Formula

We can use the following process to find a, b, and c.

Practice Questions

Question 1: Find the missing term in the quadratic sequence: 9, 16, ?, 36, 49.

Answer :


Question 2: Find the sum of the first 5 terms in the quadratic sequence: 2, 5, 10, 17, ...

Answer :

Finding the nth term of a Quadratic Sequence

Step #1: Find the sequence of first and second differences

  • Note: Make sure that the first differences are not constant and the second differences are constant to ensure that it is a quadratic sequence.

Let’s consider the following example:

Sequence: 2, 4, 8, 14, 22, …

1st Differences: 2, 4, 6, 8, …

2nd Differences: 2, 2, 2, …

As the second differences are constant, we can conclude that this is a quadratic sequence

Finding the nth term

 

Step #2: Determine a, the second difference, by dividing the second difference by 2.

  • In the above example, a = 2/2 = 1.

Quadratic Sequence Second Difference

Step #3: Write out the first three or four terms of an2 with the first three or four terms of the given sequence underneath.

an2 = 1, 4, 9, 16, …

Finding The nth Term Example

Step #4: Work out the difference between each term of an2 and the corresponding term of the given sequence.

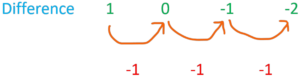
Difference between each term of an square

Step #5: Work out the linear nth term of these differences.

This is bn + c.

In the above example, we get:

bn + c = n + 2.

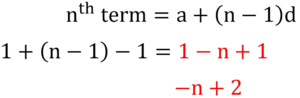
Quadratic Sequence nth term Questions

Step #6:  Add this linear nth term to an2 to obtain the nth term of the quadratic sequence.

In the above example, we have the nth term of the quadratic sequence as

an2 + bn + c = n2 – n + 2

Quadratic Sequence GCSE Example Solution

Exam Tips...

  • Before finding the nth term of a quadratic sequences, compare it to the sequence of square numbers (1, 4, 9, 16, 25, …) and look for a formula.
  • For example, in the sequence 4, 7, 12, 19, 28, …, each term is 3 more than the corresponding square number.
  • Comparing sequences to known patterns like square numbers can help identify formulas and simplify the process of finding the nth term.

Practice Questions

Question 1: Find the nth term of the quadratic sequence: 6, 15, 28, 45, ...

Answer :


Question 2: Find the missing term in the quadratic sequence: 2, 8, ?, 32, 50.

Answer :

Worksheet on Quadratic Sequence

Question 1: Find the sum of the first 6 terms in the quadratic sequence: 3, 9, 19, 33, ...



Question 2: Find the nth term of the quadratic sequence: 1, 6, 15, 28, ...



Question 3: Find the missing term in the quadratic sequence: 4, 13, ?, 37, 52.



Question 4: Find the sum of the first 8 terms in the quadratic sequence: 2, 7, 16, 29, ...