Rearranging Harder Formulae Step-by-Step Examples with Worksheet
Rearranging Harder Formulae
- Rearranging harder formulae is a valuable skill that empowers us to manipulate equations, isolate variables, and uncover deeper insights into mathematical relationships.
- This skill has practical applications across diverse fields, enabling us to solve complex problems and make informed decisions based on mathematical principles.
In this article, we will discuss:
- What is Rearranging Harder Formulae?
- Steps for Rearranging the Formula to Change the Subject of the Formula
Here is one more link to practice a few extra questions: Maths Genie Rearranging Harder Formulae Questions
What is Rearranging Harder Formulae?
- Rearranging Harder Formulae refers to the process of manipulating a given formula to make a specific variable the subject of the formula.
- This process is used extensively in mathematics and science to solve problems where it is necessary to change the variable in a formula to obtain the desired result.
Steps for Rearranging the Formula to change the Subject of Formula
- The following steps can be used to rearrange a formula to change the subject of the formula:
Step #1: Identify the variable you want to make the subject of the formula.
Step #2: Write down the given formula and identify the variable you want to make the subject.
Step #3: Isolate the variable you want to make the subject by performing inverse operations on both sides of the equation.
Step #4: Simplify the equation by performing any necessary algebraic manipulations.
Step #5: Check your answer by substituting the new expression for the variable back into the original equation to ensure it is correct.
Solved Example:
Question 1: Rearrange the formula v = u + at to make t the subject.
Solution:
- Step #1: Identify the variable you want to make the subject of the formula, which is t.
- Step #2: Write down the given formula and identify the variable you want to make the subject.
v = u + at
- Step #3: Isolate the variable t by performing inverse operations on both sides of the equation.
v = u + at
v – u = at
(t = (v – u) / a)
- Step #4: Simplify the equation by performing any necessary algebraic manipulations.
t = (v – u)/a
- Step #5: Check your answer by substituting the new expression for the variable back into the original equation to ensure it is correct.
v = u + a((v – u)/a)
v = u + v – u
v = v
The solution is correct.
Question 2: Rearrange the formula P = (4L + 2W) / 3 to make L the subject.
Solution:
- Step #1: Identify the variable you want to make the subject of the formula, which is L.
- Step #2: Write down the given formula and identify the variable you want to make the subject.
P = (4L + 2W)/3
- Step #3: Isolate the variable L by performing inverse operations on both sides of the equation.
P = (4L + 2W) / 3
3P = 4L + 2W
(4L = 3P – 2W)
(L = (3P – 2W) / 4)
- Step #4: Simplify the equation by performing any necessary algebraic manipulations.
L = (3P – 2W) / 4
- Step #5: Check your answer by substituting the new expression for the variable back into the original equation to ensure it is correct.
P = (4((3P – 2W) / 4) + 2W) / 3
P = (3P – 2W + 2W) / 3
P = P
The solution is correct.
Question 3: Make x the subject of the formula
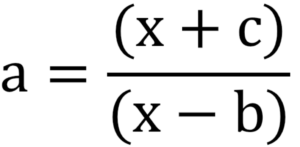
Solution:
- Step #1: Multiply both sides of the equation by (x – b) to eliminate the denominator on the right side.
a(x – b) = x + c
- Step #2: Expand the left side of the equation.
ax – ab = x + c
- Step #3: Move all the terms containing x to the left side of the equation and all the constant terms to the right side.
ax – x = ab + c
- Step #4: Factor out x on the left side of the equation.
x(a – 1) = ab + c
- Step #5: Divide both sides of the equation by (a – 1) to isolate x.
x = (ab + c) / (a – 1)
Therefore, x = (ab + c) / (a – 1) is the formula for x in terms of a, b, and c.
Conclusion
- Rearranging harder formulae is a valuable skill that empowers us to manipulate equations, isolate variables, and uncover deeper insights into mathematical relationships.
- By mastering the art of rearranging harder formulae, we develop critical thinking and problem-solving abilities that are essential for success in mathematics and scientific disciplines.
- The ability to rearrange equations allows us to simplify complex expressions, facilitating a clearer understanding of the underlying concepts and principles.
- Through the mastery of rearranging harder formulae, we unlock the potential to tackle challenging mathematical problems, optimize processes, and make accurate predictions based on mathematical relationships.
Practice Questions: Rearranging Harder Formulae
Question 1: Rearrange the formula v = πr2h to solve for h.
Question 2: Rearrange the formula A = lw + 2lh + 2wh to solve for w.
Question 3: Rearrange the formula T = 2π√(L/g) to solve for L.
Question 4: Rearrange the formula E = mc2 + mv2/2 to solve for v.
Question 5: Rearrange the formula P = 2πh + 2πr to solve for h.
Question 6: Rearrange the formula v = πr2h + (4/3)πr3 to solve for r.
Question 7: Rearrange the formula A = 2πrh + 2πr2 to solve for h.
Question 8: Rearrange the formula F = G(m1m2/r2) to solve for r.
Question 9: Rearrange the formula v = (4/3)πr3 – (4/3)πr13 to solve for r.
Question 10: Rearrange the formula A = (s/2)(a + b) to solve for b.
Solutions:
Question 1: Rearrange the formula v = πr2h to solve for h.
Solution:
Step #1: Start with the formula
v = πr2h
Step #2: Divide both sides by πr2
v / (πr2) = h
The rearranged formula is:
h = v / (πr2)
Question 2: Rearrange the formula A = lw + 2lh + 2wh to solve for w.
Solution:
Step #1: Begin with the formula
A = lw + 2lh + 2wh
Step #2: Subtract lw and 2lh from both sides.
A – lw – 2lh = 2wh
Step #3:Factor out w on the right side.
A – lw – 2lh = w(2h)
Step #4: Divide both sides by (2h).
(A – lw – 2lh) / (2h) = w
The rearranged formula is:
w = (A – lw – 2lh) / (2h)
Question 3: Rearrange the formula T = 2π√(L/g) to solve for L.
Solution:
Step #1:Start with the formula
T = 2π√(L/g)
Step #2:Divide both sides by 2π.
T / (2π) = √(L/g)
Step #3: Square both sides of the equation.
(T / (2π))2 = L/g
Step #4: Multiply both sides by g.
g(T / (2π))2 = L
The rearranged formula is:
L = g(T / (2π))2
Question 4: Rearrange the formula E = mc2 + mv2/2 to solve for v.
Solution:
Step #1: Begin with the formula
E = mc2 + mv2/2
Step #2:Subtract mc2 from both sides
E – mc2 = mv2/2
Step #3:Multiply both sides by 2/m.
(2/m)(E – mc2 ) = v2
Step #4: Take the square root of both sides.
√[(2/m)(E – mc2)] = v
The rearranged formula is:
v = √[(2/m)(E – mc2)]
Question 5: Rearrange the formula P = 2πh + 2πr to solve for h.
Solution:
Step #1:Start with the formula
P = 2πh + 2πr
Step #2:Subtract 2πr from both sides.
P – 2πr = 2πh
Step #3:Divide both sides by 2π.
(P – 2πr) / (2π) = h
The rearranged formula is:
h = (P – 2πr) / (2π)
Question 6: Rearrange the formula v = πr2h + (4/3)πr3 to solve for r.
Solution:
Step #1:Begin with the formula
v = πr2h + (4/3)πr3
Step #2:Subtract (4/3)πr3 from both sides.
v – (4/3)πr3 = πr2h
Step #3:Divide both sides by πh.
(v – (4/3)πr3) / (πh) = r2
Step #4: Take the square root of both sides.
√[(V – (4/3)πr3) / (πh)] = r
The rearranged formula is:
r = √[(V – (4/3)πr3) / (πh)]
Question 7: Rearrange the formula A = 2πrh + 2πr2 to solve for h.
Solution:
Step #1: Start with the formula
A = 2πrh + 2πr2
Step #2: Subtract 2πr2 from both sides.
A – 2πr2 = 2πrh
Step #3: Divide both sides by 2πr.
(A – 2πr2) / (2πr) = h
Step #4: Simplify the expression on the left side.
A/(2πr) – r = h
The rearranged formula is:
h = A/(2πr) – r
Question 8: Rearrange the formula F = G(m1m2/r2) to solve for r.
Solution:
Step #1: Begin with the formula
F = G(m1m2/r2)
Step #2: Multiply both sides by r2.
Fr2 = G(m1m2)
Step #3: Divide both sides by F.
r2 = G(m1m2)/F
Step #4: Take the square root of both sides.
r = √(G(m1m2)/F)
The rearranged formula is:
r = √(G(m1m2)/F)
Question 9: Rearrange the formula v = (4/3)πr3 – (4/3)πr13 to solve for r.
Solution:
Step #1: Start with the formula
v = (4/3)πr3 – (4/3)πr13
Step #2: Add (4/3)πr13 to both sides.
v + (4/3)πr13 = (4/3)πr3
Step #3: Multiply both sides by 3/(4π).
(3/(4π))(v + (4/3)πr13) = r3
Step #4: Take the cube root of both sides.
r = ∛[(3/(4π))(v + (4/3)πr13)]
The rearranged formula is:
r = ∛[(3/(4π))(v + (4/3)πr13)]
Question 10: Rearrange the formula A = (s/2)(a + b) to solve for b.
Solution:
Step #1: Begin with the formula
A = (s/2)(a + b)
Step #2: Divide both sides by (s/2).
A / (s/2) = a + b
Step #3: Simplify the expression on the left side.
2A / s = a + b
Step #4: Subtract a from both sides.
(2A / s) – a = b
The rearranged formula is:
b = (2A / s) – a

