Sketching Quadratic Graphs Step-by-Step Examples
Sketching Quadratic Graphs
- Quadratic functions are an important part of mathematics, and graphing them is a crucial thing every learner or anyone involved in using mathematics should be in a position to do.
- Similar to parabola, Quadratic graphs show the pattern of the quadratic equation and present much more information about the function.
In this article, we will discuss:
- What is Sketching Quadratic Graphs?
- Key Points on a Quadratic Graph
- How to Sketch a Quadratic Graph
Here is one more link to practice a few extra questions: Maths Genie Sketching Quadratic Graphs Questions
What is Sketching Quadratic Graphs?
- A quadratic graph is the geometric representation of a quadratic equation which can also be written as f(x) = ax2 + bx + c where a, b and c are constants.
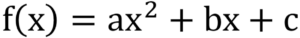
- Quadratic graphs are graphs of quadratic functions that resemble the letter ‘U’ and can either be a ‘U’ shape that opens up or down depending on the sign of ‘a’.
- These are usual properties and characteristics of any quadratic graph, including vertex, symmetry axis, and intercepts.
Key Points on a Quadratic Graph
Vertex:
- The vertex is the coordinate point for the graph which is the lowest point in the case of an up turned parabola or the highest point in the case of a down turned parabola.
- In the quadratic function of the form:
f(x) = ax2 + bx + c,
the x-coordinate of the vertex is given by the formula
x = -b/(2a).
- The other value of the y-axis can then be determined by putting in the value of the x-coordinate into the original equation.
Axis of Symmetry:
- The axis of symmetry is a down-line passing through the vertex, which as well bisects the parabola into two equal halves.
- The equation of the axis of symmetry is x = -b/(2a)
Intercepts:
- For quadratic graphs, the x-intercepts or intercepts points are the points at which they cross the x- axis. These are the values of x for which f(x) = 0.
- The y-intercept, denoted by the point (0,c). it is the point where the graph of a function line crosses the y axis.
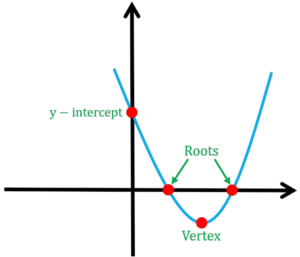
Direction of Opening:
- Quadratic function shows the direction of the opening according to the coefficient ‘a.’ This indicates that if variable ‘a’ is positive the parabola face will be upward bending whereas if the variable ‘a’ is negative the parabola face will be downward bending.
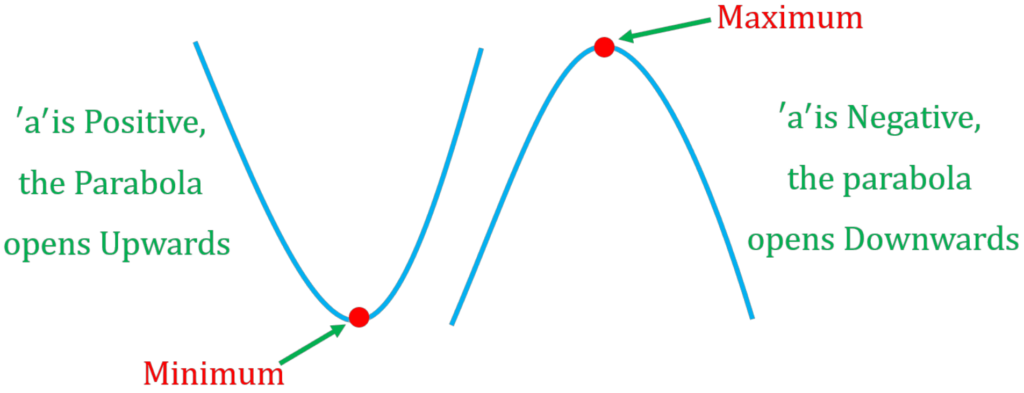
How to Sketch a Quadratic Graph
Identify Key Parameters:
- Let’s find out what values corresponds ‘a,’ ‘b,’ and ‘c’ from the following quadratic function.
- These are values that you can use to determine vertex, axis of symmetry and intercepts.
Plot the Vertex:
- To find the x-coordinate of the vertex, we need to use the formula x = -b/(2a).
- Plug in this value into the original equation to get the y-coordinate that corresponds to it.
- Locate the vertex from the graph.
Draw the Axis of Symmetry:
- The axis of symmetry can be found with the help of the given equation, x = (-b/2a).
- Place a vertical line at the vertex that will show the parabola’s axis of symmetry.
Plot Intercepts:
- Locate the x-intercept(s) by putting f(x) = 0 and solving for x.
- The y-intercept is the value of y when x = 0.
- Plot these points on the graph.
Sketch the Parabola:
- Join the plotted points so as to form a smooth curve that would be that of a parabola.
- Note the sign of ‘a’ in the opening that dictates a change in direction.
Solved Example:
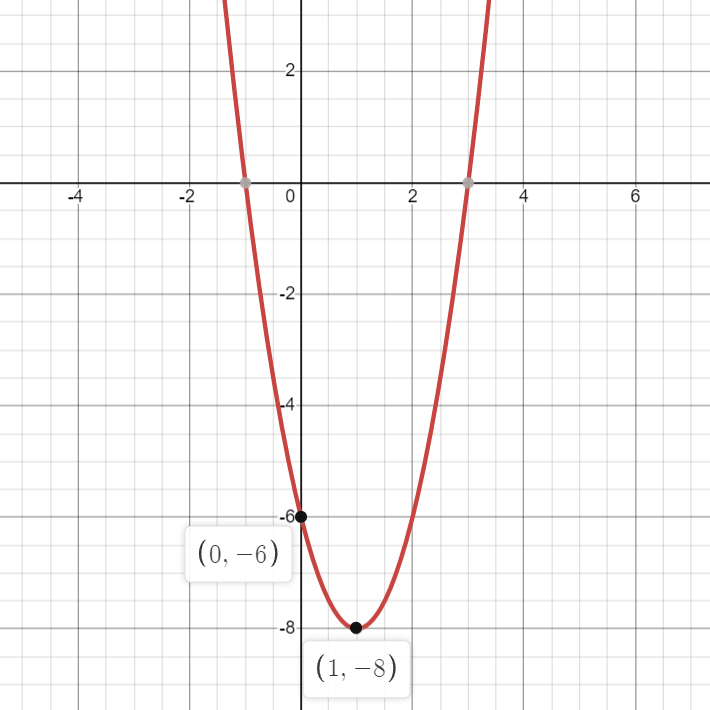
Question 1: Sketch the graph of the quadratic function f(x) = 2x2 – 4x – 6.
Solution:
- Step #1: Identify Key Parameters:
a = 2, b = -4, c = -6.
- Step #2: Plot the Vertex
Use the formula
x = -b/(2a)
= -(-4)/(2 x 2)
= 1.
Substitute x = 1 into f(x) to find y:
f(1) = 2(1)2 – 4(1) – 6
= -8.
Vertex coordinates: (1, -8).
- Step #3: Draw the Axis of Symmetry:
The axis of symmetry is x = 1.
- Step #4: Plot Intercepts:
x-intercepts:
Set f(x) = 0 → 2x2 – 4x – 6 = 0.
Solve using factoring or quadratic formulas to find x-values.
y-intercept:
Set x = 0 → f(0) = -6.
- Step #5: Sketch the Parabola:
Connect the vertex and intercepts to form the parabola. Since ‘a’ is positive, the parabola opens upwards.
Conclusion
- Drawing quadratic graphs could be used as a graphical method of analyzing the behaviour of quadratic functions.
- That is the reason why it is necessary to find the vertex, axis of symmetry, intercepts, and the direction in which the parabola opens.
- Quadratic graphs are graphical representations of quadratic functions that can help better comprehend their behaviour.
- The skill of sketching quadratic graphs is relevant and can be used in solving problems in physics, engineering, economy and many other sciences.
Practice Questions: Sketching Quadratic Graphs
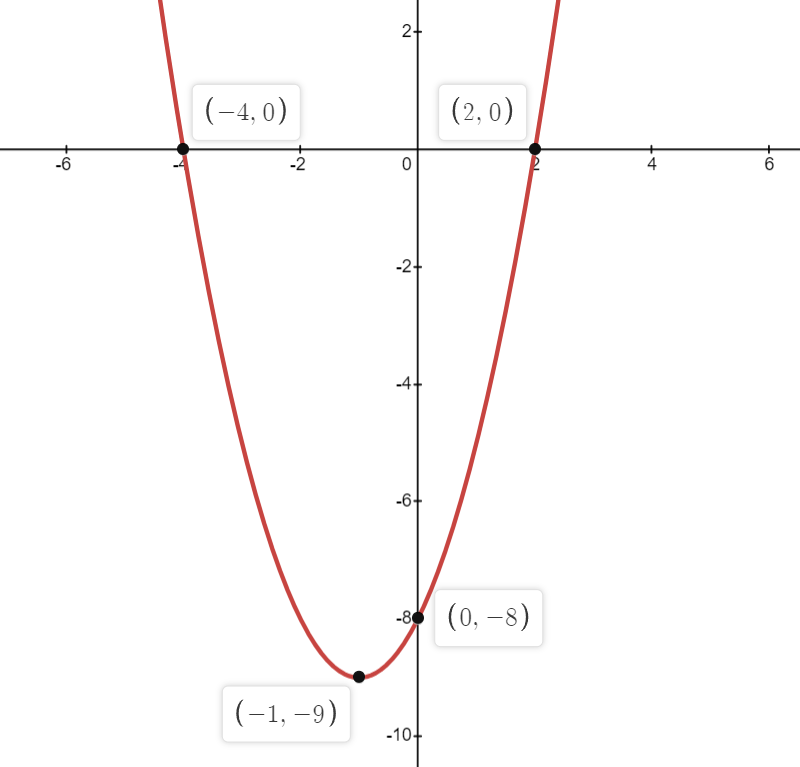
Question 1: Sketch the following graphs y = x2 + 6x + 8
Question 2: Sketch the following graphs y = x2 – x – 6
Question 3: Sketch the following graphs y = x2 + 6x + 9
Question 4: Sketch the following graphs y = x2 – 13x + 42
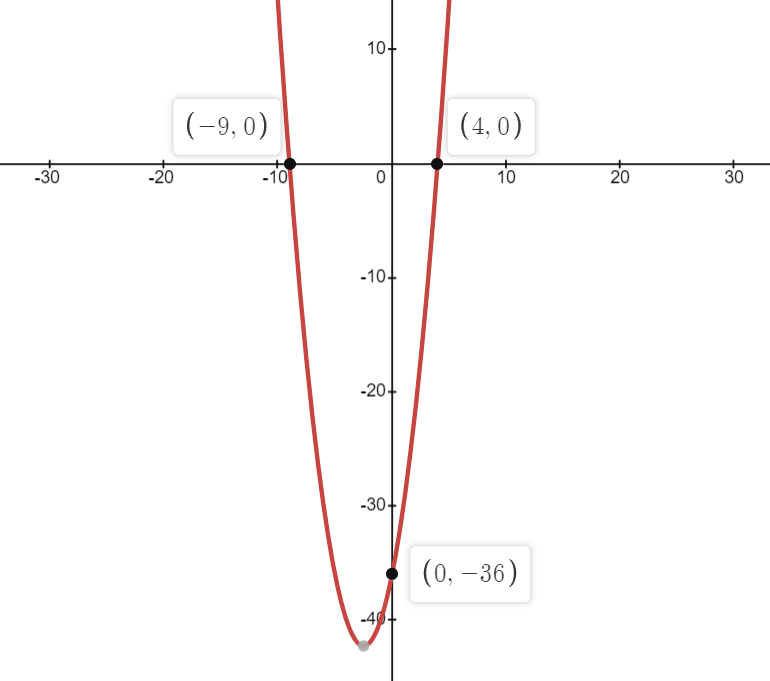
Question 5: Sketch the following graphs y = x2 + 5x – 36
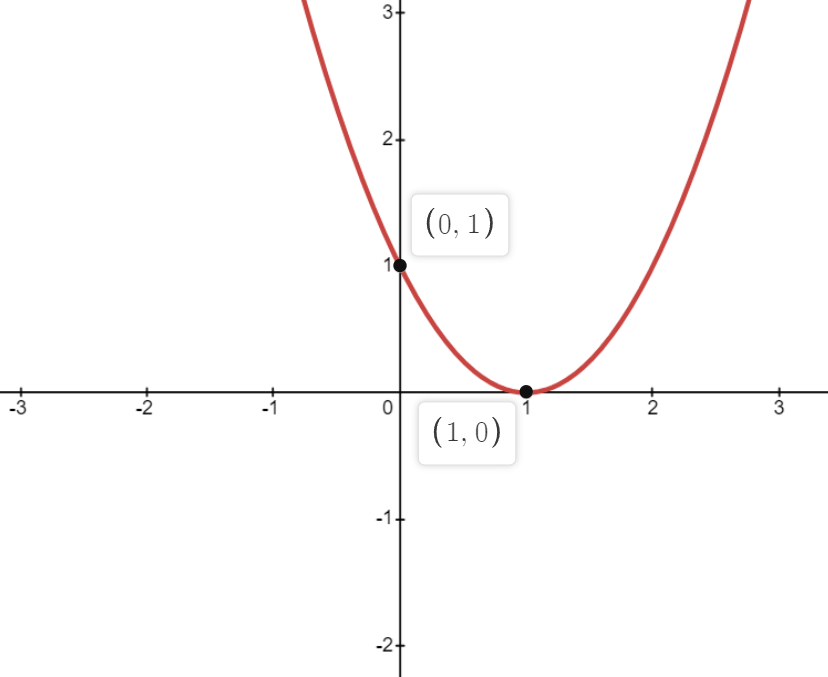
Question 6: Sketch the following graphs y = x2 – 2x + 1
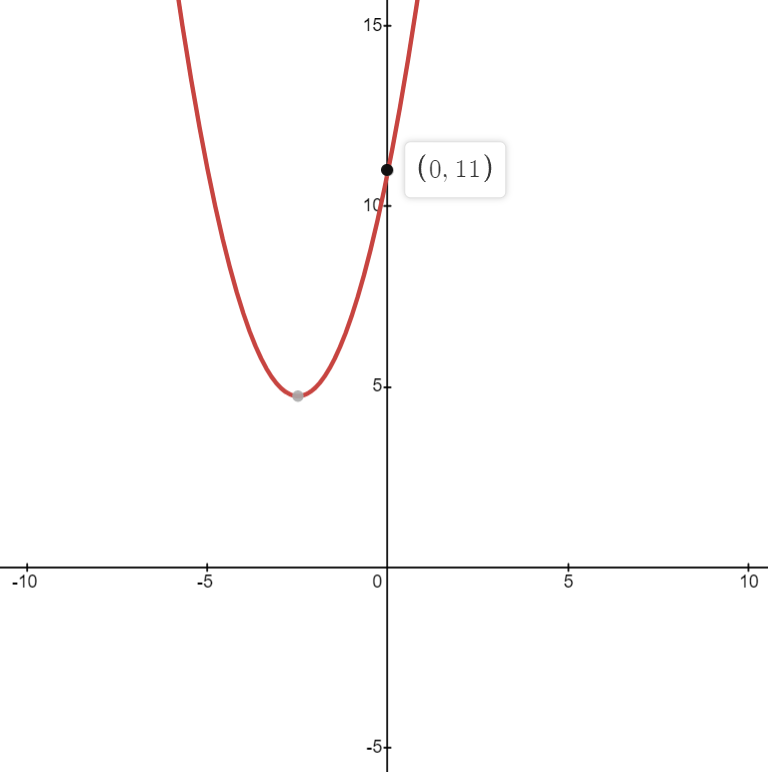
Question 7: Sketch the following graphs y = x2 + 5x + 11
Question 8: Sketch the following graphs y = x2 – 4x + 7
Question 9: Sketch the following graphs y = x2 + 4x
Question 10: Sketch the following graphs y = x2 + 2x – 8
Solutions:
Question 1: Sketch the following graphs y = x2 + 6x + 8
Solution:
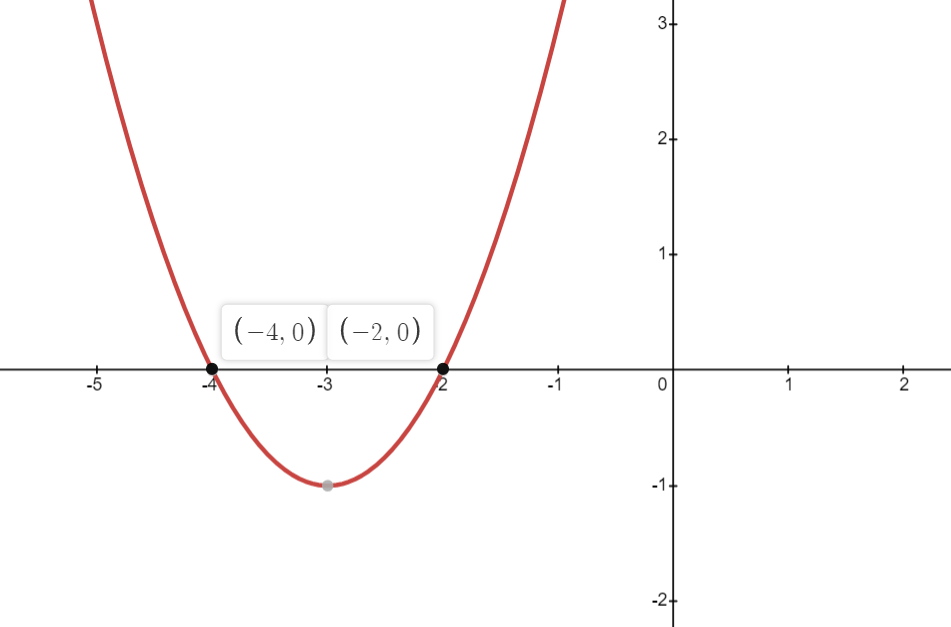
Question 2: Sketch the following graphs y = x2 – x – 6
Solution:
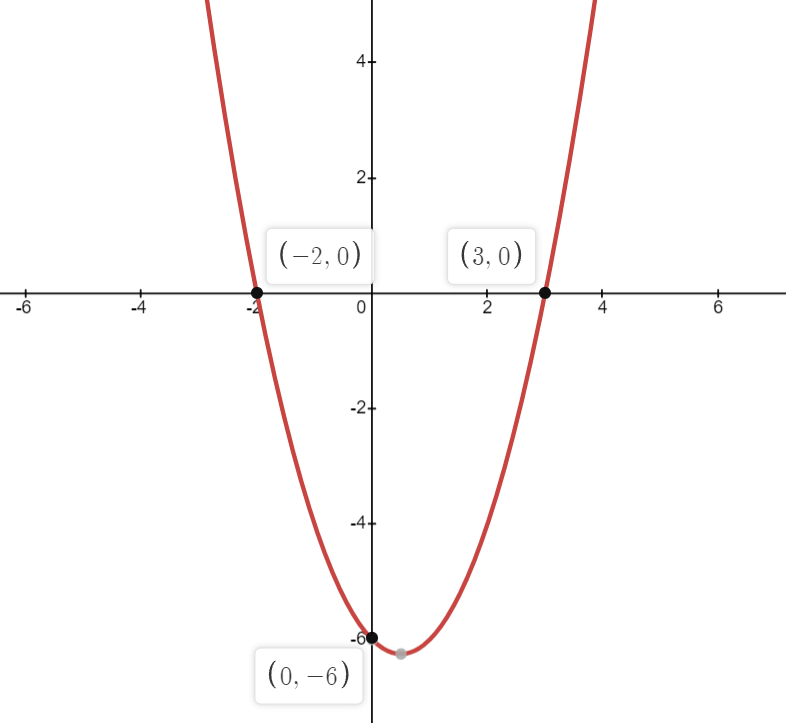
Question 3: Sketch the following graphs y = x2 + 6x + 9
Solution:
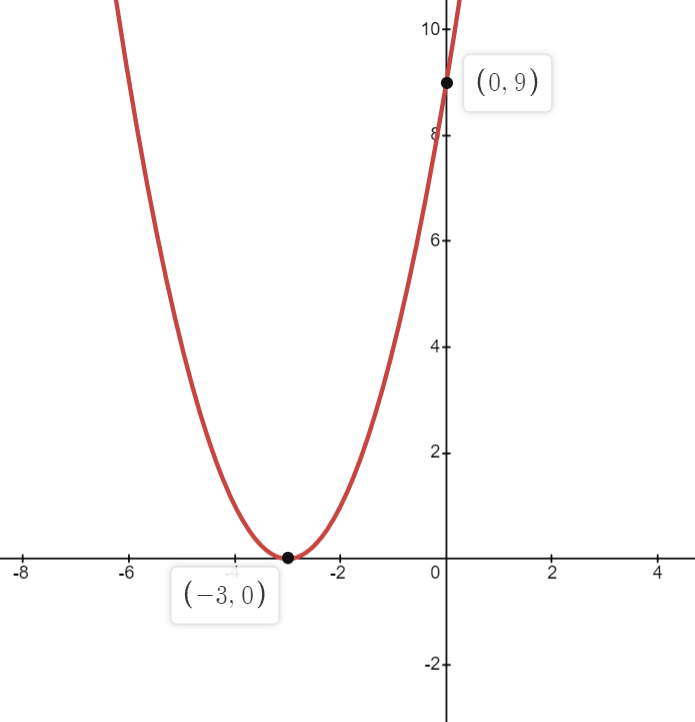
Question 4: Sketch the following graphs y = x2 – 13x + 42
Solution:
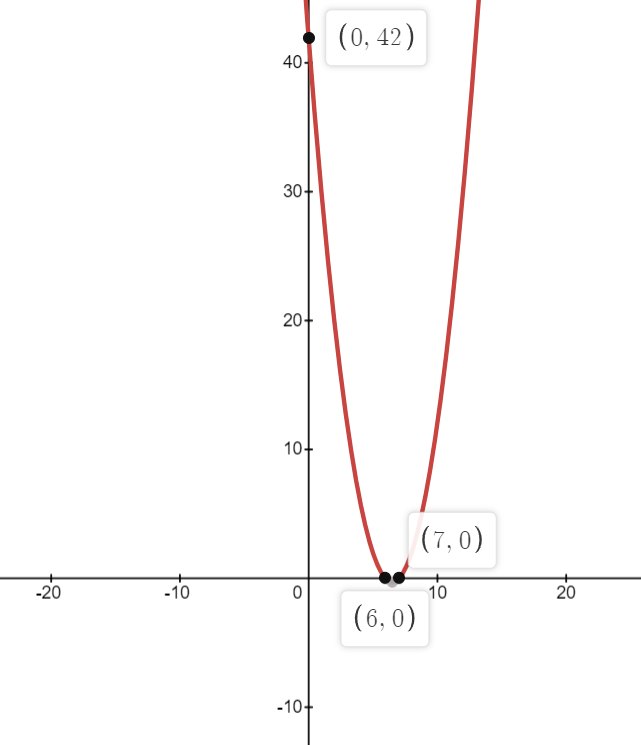
Question 5: Sketch the following graphs y = x2 + 5x – 36
Solution:
Question 6: Sketch the following graphs y = x2 – 2x + 1
Solution:
Question 7: Sketch the following graphs y = x2 + 5x + 11
Solution:
Question 8: Sketch the following graphs y = x2 – 4x + 7
Solution:
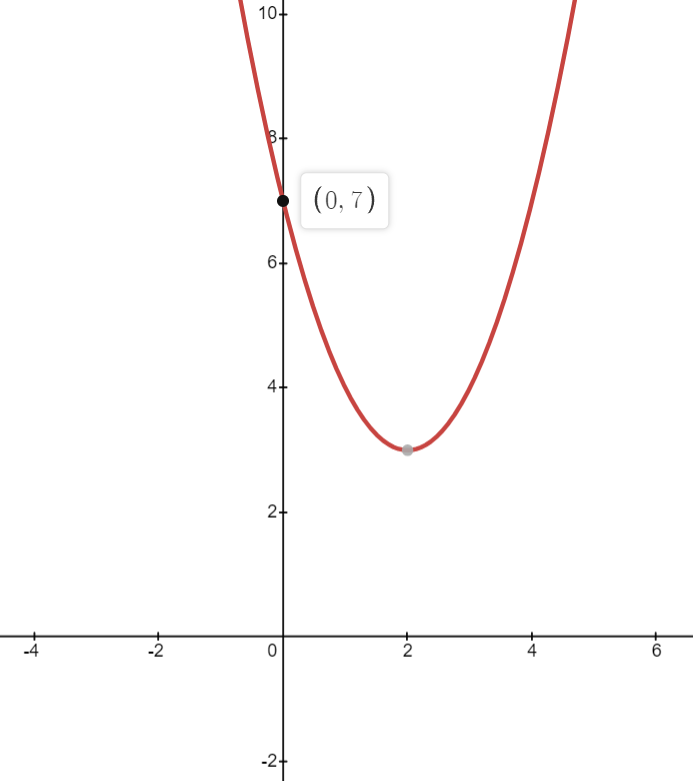
Question 9: Sketch the following graphs y = x2 + 4x
Solution:
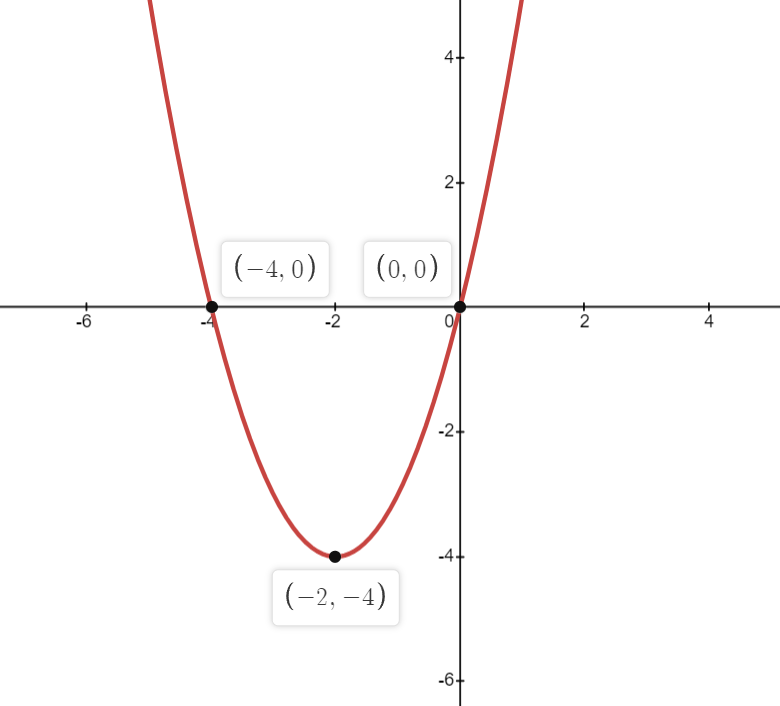
Question 10: Sketch the following graphs y = x2 + 2x – 8
Solution: