Quadratic Simultaneous Equations: Examples with Worksheet

Calculator
Test Yourself

Quadratic Simultaneous Equations

  • Quadratic simultaneous equations involve two equations with two variables, one of which is a quadratic equation and the other is a linear equation.
  • These equations are used in algebraic problems to find the value of two unknown variables.

In this article, we will discuss: 

  1. What are Quadratic Simultaneous equations?
  2. How to solve Quadratic Simultaneous Equations using Factorisation?
  3. How to Solve Quadratic Simultaneous Equations by Graphs?

Here is one more link to practice a few extra questions: Maths Genie Quadratic Simultaneous Equations Questions

What are Quadratic Simultaneous equations?

  • One common form of quadratic simultaneous equations is:

ax² + bx + c = 0 (quadratic equation)

dx + ey + f = 0 (linear equation)

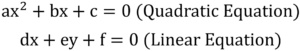
Quadratic Simultaneous Equations Formulas

  • To solve quadratic simultaneous equations by factorisation, we need to follow these steps:
    1. Rearrange the equations so that one variable is the same in both equations.
    2. Use the linear equation to solve for the variable in terms of the other variable.
    3. Substitute the expression for the variable into the quadratic equation.
    4. Factorise the quadratic expression and solve for the remaining variable.
    5. Substitute the value of the variable into the expression found in step 2 to find the value of the other variable.

How to solve Quadratic Simultaneous Equations using Factorisation

  • To solve quadratic simultaneous equations by factorisation, follow these steps:

Step #1: Rearrange the linear equation to solve for one of the variables.

For example, if the linear equation is 2x – 3y = 7,

solve for y:

y = (2x – 7)/3.

Step #2: Substitute the value of y into the quadratic equation, resulting in a quadratic equation in terms of x.

For example, if the quadratic equation is x2 – 5x + 6 = 0,  substitute (2x – 7)/3 for y to get

(2x – 7)2/9 – 5(2x – 7)/3 + 6 = 0.

Step #3: Simplify the quadratic equation and solve for x. In the example above,

we can simplify the equation to

4x2 – 38x + 65 = 0.

Factor the quadratic equation to get

(2x – 5)(2x – 13) = 0.

Therefore, x = 5/2 or x = 13/2.

Step #4: Substitute the value of x back into the linear equation to solve for y.

In the example above, if x = 5/2, then y = (2(5/2) – 7)/3 = -1/3.

If x = 13/2, then y = (2(13/2) – 7)/3 = 5/3.

Therefore, the solution for the quadratic simultaneous equations

x2 – 5x + 6 = 0 and 2x – 3y = 7 is (5/2, -1/3) and (13/2, 5/3).

How to Solve Quadratic Simultaneous Equations by Graphs

  • Another way to solve quadratic simultaneous equations is by using graphs.
  • This method involves graphing the two equations on the same coordinate plane and finding the intersection points.
  • The intersection points are the solutions to the system of equations.
  • To graph the equations, we need to first rewrite them in slope-intercept form,

    y = mx + b

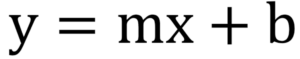
Linear Equation Formula

For the linear equation,

ax + by + c = 0,

Quadratic Simultaneous Equations Formula

we can solve for y to get:

y = (-ax – c)/b

For the quadratic equation, y = ax2 + bx + c, we can use a graphing calculator or plotting points to create a graph.

  • Once we have both equations in slope-intercept form, we can plot them on the same coordinate plane. The solutions to the system of equations are the intersection points of the two graphs.
Request for Demo Lesson

certified Physics and Maths tutor

 

 

Solved Example: 

Question 1: How can we solve the system of equations consisting of a quadratic equation (3x2 – 4x – 5 = 0) and a linear equation (2x – 7y + 1 = 0)?

Solution: 

To solve the system of equations, we will follow these steps:

  • Step #1: Begin by rewriting the linear equation in slope-intercept form:

2x – 7y + 1 = 0

-7y = -2x – 1

y = (2/7)x + 1/7

  • Step #2: Graph both equations on the same coordinate plane. The solutions to the system of equations are the intersection points of the two graphs.
  • Step #3: Observe the graph to identify the intersection points, which represent the solutions to the system.
  • Step #4: From the graph, we can see that there are two intersection points, approximately

(1.5, 1.1) and (-0.6, -0.4).

  • Step #5: Therefore, the solutions to the system of equations are:

For the point (1.5, 1.1):

x ≈ 1.5

y ≈ 1.1

For the point (-0.6, -0.4):

x ≈ -0.6

y ≈ -0.4

These solutions represent the values of x and y that satisfy both the quadratic and linear equations in the system.

Practice Questions

Question 1. Solve the simultaneous equations:

x2 - 3x - 4 = 0

y2 - 4y - 5 = 0

Answer : ( , )


Question 2: Solve the simultaneous equations

x2 - 9 = 0

y2 - 4y - 21 = 0

Answer : ( , )

Conclusion

  • Quadratic simultaneous equations involve two equations, one of which is a quadratic equation.

  • The goal is to find the values of the variables that satisfy both equations.

  • There are two main methods to solve quadratic simultaneous equations: factorisation and graphing.

  • Factorisation involves factoring both equations and setting each factor equal to zero to find the solutions.

  • Graphing the two equations allows us to visually determine the points where they intersect, which represent the solutions.

  • Understanding the basics of quadratic simultaneous equations and the methods used to solve them is important for students.

  • Being proficient in solving these equations can boost confidence when encountering similar problems in exams or real-life situations.

Worksheet on Quadratic Simultaneous Equations

Question 1: Solve the simultaneous equations

2x + y = 7

x2 - y2 = 8

)

Question 2: Solve the simultaneous equations

x2 + y2 = 20

y = x + 3

)

Question 3: Solve the simultaneous equations

2x2 + y2 = 10

2x - y = 5

)

Question 4: Solve the simultaneous equations

y = x2 + x - 7

4x + 2y + 1 = 0

)

Question 5: Solve the simultaneous equations

y = x - 2

2x2 - xy = 11

)