Congruent Triangles: Rules and Step-by-Step Examples

Congruent Triangles

Congruent triangles are one of the main concepts in geometry; they are the first step to understanding the equality and similarity of geometric shapes.
“Congruent” here implies that the two triangles are the same shape and size which is a fundamental concept but also very useful in so many ways in mathematics.
Verifying of congruent triangles is the main part of the geometry which together with criteria and set of techniques underlies the whole process of geometric reasoning.

In this article, we will discuss:

Here is one more link to practice a few extra questions: Maths Genie Congruent Triangles Questions

What are Congruent Triangles?

Two triangles of identical size and shape constitute a pair of congruent ones having the same length and corresponding angles.
Symbolically, in congruent case triangle ABC and triangle DEF is denoted as ∆ABC ≅ ∆DEF.
Congruence implies that the corresponding parts of the triangles are equal: if both preceding sides are equal, and the given angles are equal in length also.
The statement about the congruent triangles means that this is a symbol that represents triangles that are the same in size and shape.

Side-Angle-Side (SAS) Criterion:

- Upon condition that two sides and an included angle of one triangle coincide with a corresponding sides and angle of the other triangle, the triangles are congruent.

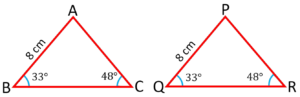
Angle-Side-Angle (ASA) Criterion:

- If two angles and the side opposite one of them are equal in size and position to the angles and opposite side of another triangle, the triangles are congruent.

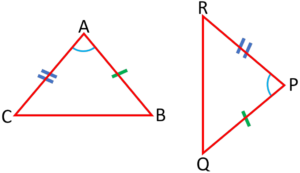
Side-Side-Side (SSS) Criterion:

- If each of the three sides of one triangle is the same as all of the three sides of the second triangle, these two triangles are congruent.

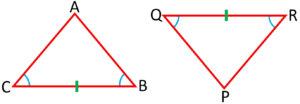
Angle-Angle-Side (AAS) Criterion:

- If angles and non-included side of one triangle are equal to corresponding angles and side of another triangle, the triangles are congruent.

Right angle- Hypotenuse-Side (RHS) Criterion:

- If one right-angled triangle’s hypotenuse and one of its sides is equal to the hypotenuse and a side of another right-angled triangle, we can declare them congruent using the RHS (Right-Angle, Hypotenuse, Side) rule.

Compare matching angles and sides.
Determine if the shapes are identical.
If they are congruent, specify the congruence condition that applies to the pair of triangles.

Solved Example:

Question : Consider two triangles, ∆ABC and ∆PQR, where AB = PQ, BC = QR, and ∠B = ∠Q. Prove that ∆ABC ≅ ∆PQR.

Solution:

AB = PQ (Side)

BC = QR (Side)

∠B = ∠Q (Angle)

We have two sides and the included angle equal in both triangles.

By the SAS criterion, ∆ABC ≅ ∆PQR.

The SAS, ASA, SSS, AAS, and RHS criteria are very the important instruments of the proof of the triangle with similar angles and sides by the congruency theory.
Validity triangles act as fundamental assembly units for complicated geometric deductions and figures.
Congruent triangles sheer concern is not limited to pure theoretical geometry but it has applied also in various disciplines as well.
Acquiring proficiency in congruent triangles lay a groundwork for a more complex view of geometric features, for instance, connecting dots between different spatial dimensions.

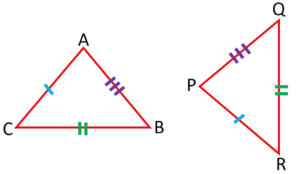
Question 1: Identify the congruence condition satisfied by this pair of identical triangles.

Question 2: Identify the congruence condition satisfied by this pair of identical triangles.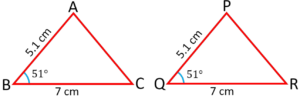

Question 3: Identify the congruence condition satisfied by this pair of identical triangles.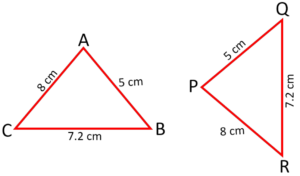

Question 4: Identify the congruence condition satisfied by this pair of identical triangles.