Composite and Inverse Functions Examples With Worksheet

Calculator
Test Yourself

Composite and Inverse Functions

Request for Demo Lesson
  • Functions are mathematical rules that map one set of values (input) to another set of values (output). In mathematics, two types of functions are commonly used: inverse and composite functions.
  • Understanding and applying these concepts enhance problem-solving skills and provide valuable tools for various fields of study.

In this article, we will discuss: 

  1. What are Composite and Inverse Functions?
  2. Steps for Finding the Composite and Inverse of a Function

Here is one more link to practice a few extra questions: Maths Genie Composite and Inverse Functions Questions

What is an Inverse Function?

  • An inverse function is a function that reverses the output of another function.
  • In other words, if we have a function f(x) that maps an input value x to an output value y, then the inverse function f⁻¹(x) maps the output value y back to the input value x.
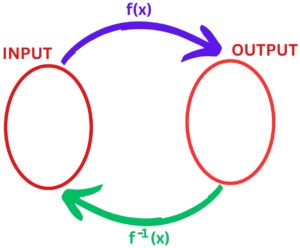
Composite and Inverse Functions diagram
  • The inverse function of f is denoted by f⁻¹.

Steps for Finding the Inverse of a Function

  • To find the inverse of a function, follow these steps:

Step #1: Replace f(x) with y.

Step #2: Interchange x and y.

Step #3: Solve for y in terms of x.

Step #4: Replace y with f⁻¹(x).

certified Physics and Maths tutor

 

 

Solved Example: 

Question 1: Let f(x) = 3x + 4. To find the inverse of this function.

Solution: 

we follow the steps:

  • Step #1: Replace f(x) with y.

y = 3x + 4

  • Step #2: Interchange x and y.

x = 3y + 4

  • Step #3: Solve for y in terms of x.

y = (x – 4)/3

  • Step #4: Replace y with f⁻¹(x).

f⁻¹(x) = (x – 4)/3

Practice Questions

Question 1: Determine the inverse of the function represented by f(x) = 4x - 3.

Answer :


Question 2: Consider the function g(x) = 2x - 5. Find the inverse of this function.

Answer :

What is a Composite Function?

  • A composite function is a function that is obtained by combining two or more functions.
  • The output of one function becomes the input of another function.
  • The composite function is denoted by (f ∘ g)(x), which means “f of g of x”.
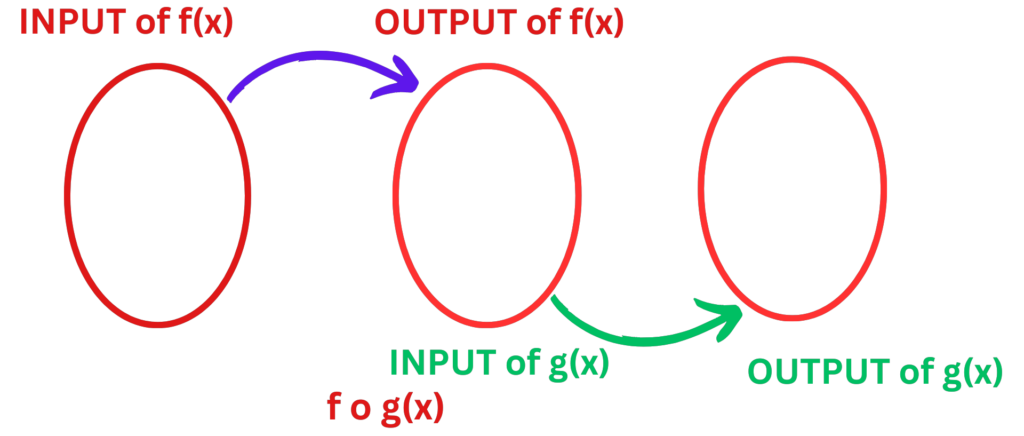
Composite and Inverse Functions Worksheet Question

Steps for Finding the Composite of a Function

  • To find the composite of a function, follow these steps:

Step #1: Apply the first function to the input value.

Step #2: Take the output of the first function and apply the second function to it.

Step #3: Simplify the expression.

certified Physics and Maths tutor

 

 

Solved Example: 

Question 1: Let f(x) = x² and g(x) = x – 1. To find (f ∘ g)(x)

Solution: 

we follow the steps:

  • Step #1: Apply g(x) to the input value.

g(x) = x – 1.

  • Step #2: Take the output of g(x) and apply f(x) to it.

f(g(x)) = (x – 1)²

  • Step #3: Simplify the expression.

f(g(x)) = x² – 2x + 1.

Practice Questions

Question 1: Let f(x) = 2x - 1 and g(x) = x2 + 1. Find the composite function (g ∘ f)(x) and simplify it.

Answer :


Question 2: Let f(x) = 2x + 3 and g(x) = x2 - 2x. Find the composite function (g ∘ f)(x) and simplify it.

Answer :

Conclusion

  • In conclusion, inverse and composite functions are fundamental concepts in mathematics that allow us to reverse the effect of a function and combine multiple functions to analyze complex relationships.
  • Understanding and applying these concepts enhance problem-solving skills and provide valuable tools for various fields of study.
  • Mastery of inverse and composite functions is essential for advancing in higher-level mathematics and related disciplines.

Worksheet on Composite and Inverse Functions

Question 1: Let f(x) = 3x + 2 and g(x) = 5x - 1. Find f(g(x)).



Question 2: Let f(x) = x² - 5x + 6 and g(x) = 2x + 1. Find f(g(x)).



Question 3: Let f(x) = 3x - 4. Find f⁻¹(x).



Question 4: Let f(x) = 2x - 1 and g(x) = 3x + 2. Find g(f(x)).