Simultaneous Equations - GCSE Maths
Introduction
- Two or more equations are solved together at the same time.
- A solution of these equation is the value of variables which satisfy both of the equations.
Examples:
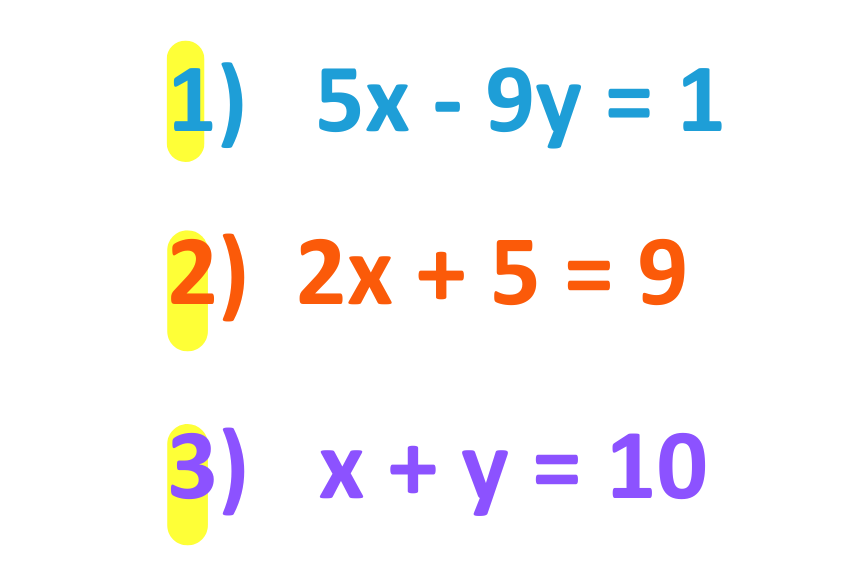
Types of Simultaneous Equations
- Simultaneous equations can be linear (where variables are raised to the power 1) or non linear (exponent more than 1)
- Solution of Simultaneous equation: values of variables that satisfy both the equations.
- Simultaneous equations are used in various fields like mathematics, physics, computer science and economics.

Methods to Solve Simultaneous Equations
There are two methods to solve Simultaneous Equations-
- Elimination method: In this method, we eliminate one of the variables by adding or subtracting the equations, which results in a simpler equation with only one variable.
- Substitution method : In this method one variable is expressed in terms of the other variable and then its value is substituted in other equation, which results in a simpler equation with one variable.
Steps to Solve Simultaneous Equations by Elimination Method
Elimination method
Let us solve the following simultaneous equations step by step using the elimination method:
Step#1: Identify the variable that can be eliminated :
We can see that if we multiply the 2nd equation with 2 then the coefficient of x in both the equations will become equal and then it can be eliminated by subtraction :
2x + 3y = 5 …(1)
1x – 1y = 0 …(2)
Step#2: Add or subtract the equations to get a combined equation with only one variable:
Here, one variable (x) will get eliminated if we subtract equation 2 from 1:
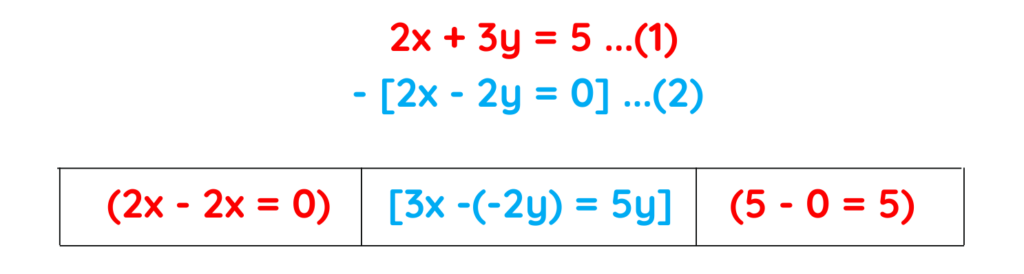
The combined equation is:
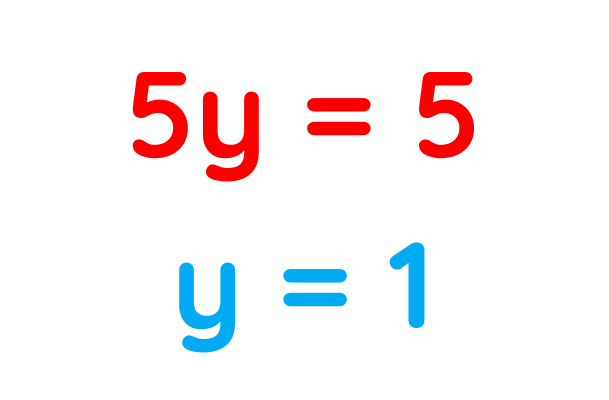
Step#3: Use the known variable’s value to find the other variable’s value :
Pick one of the simultaneous equations and put the value of y in it –

So, the solution of these simultaneous equations is:

Steps to Solve Simultaneous Equations by Substitution Method
Substitution method:
Let us solve the pair of Simultaneous equations by using Substitution method :
Step#1: Find one variable’s value in the form of the other variable:
Example: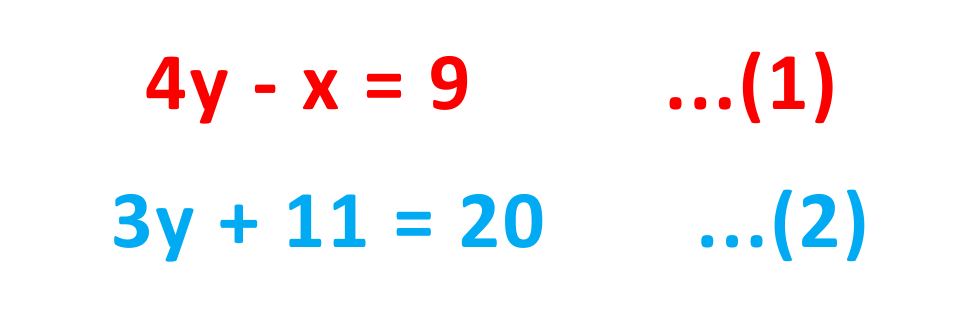
From 1st Equation: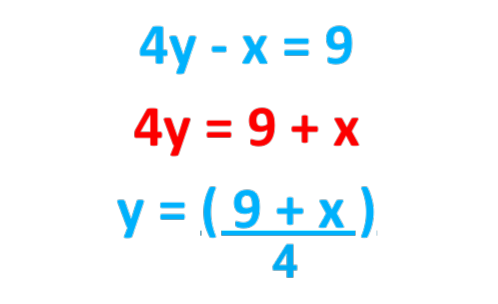
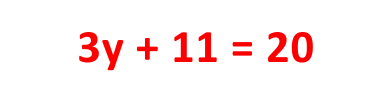
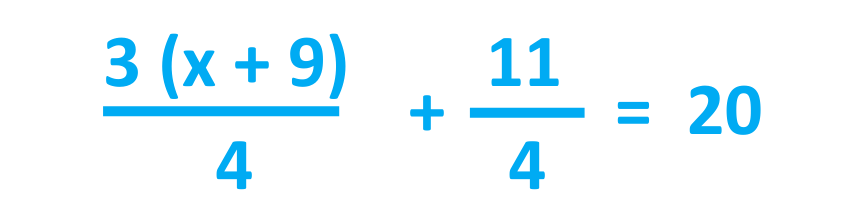
Taking LCM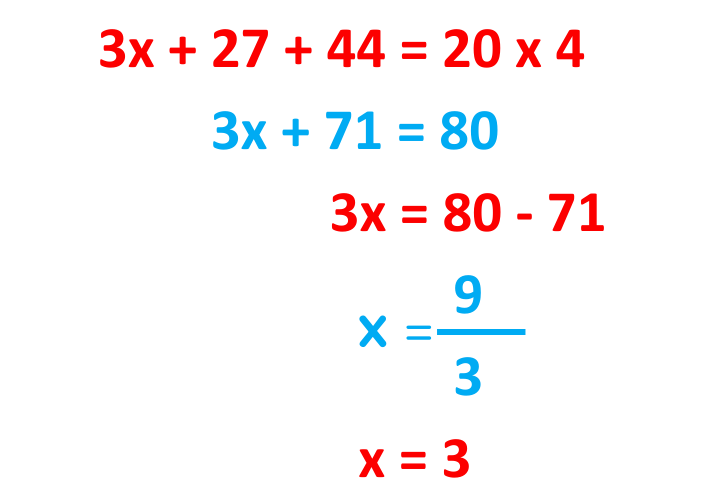
Step#3: Use the known value of one variable to find the value of the other-
Pick one of the original Equations:
From 1st Equation, put x=3,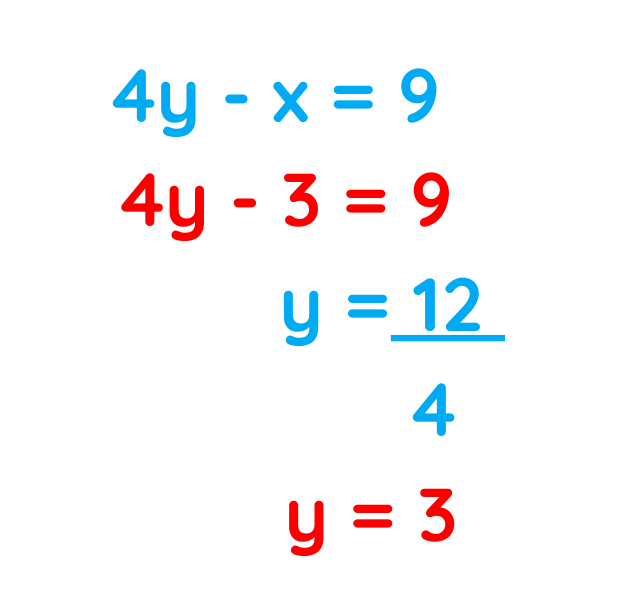
x=3 and y=3
 Solved Example:
Solved Example:
Problem: Solve the following pair of Simultaneous equations by using the Elimination method.
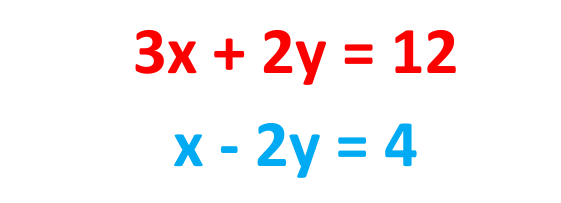
Solution:
Step#1: Identify the variable that can be eliminated:
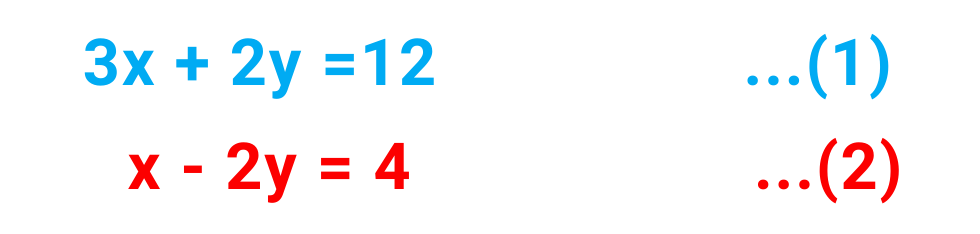
Multiply equation 2nd by 3 so that the coefficients of x in both the equations become equal.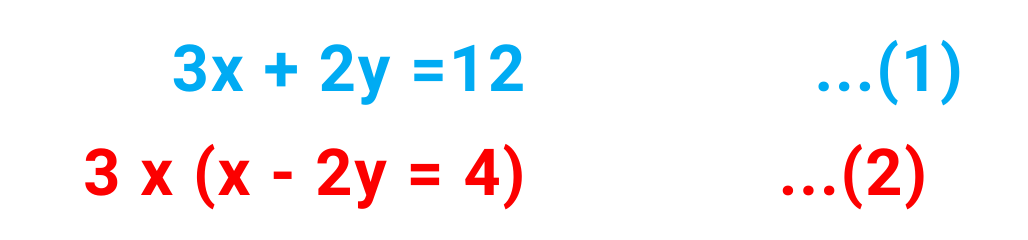
The resulting equations are: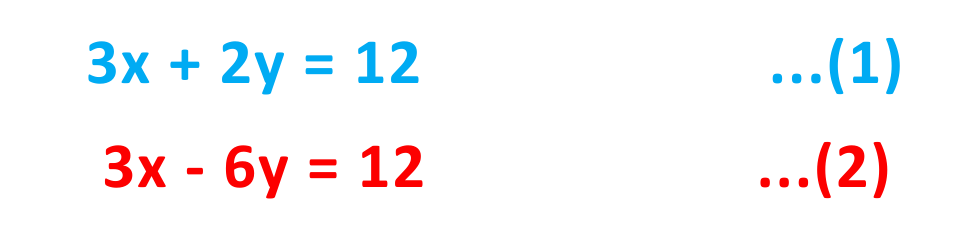
Step#2: Subtract the 2nd equation from the 1st: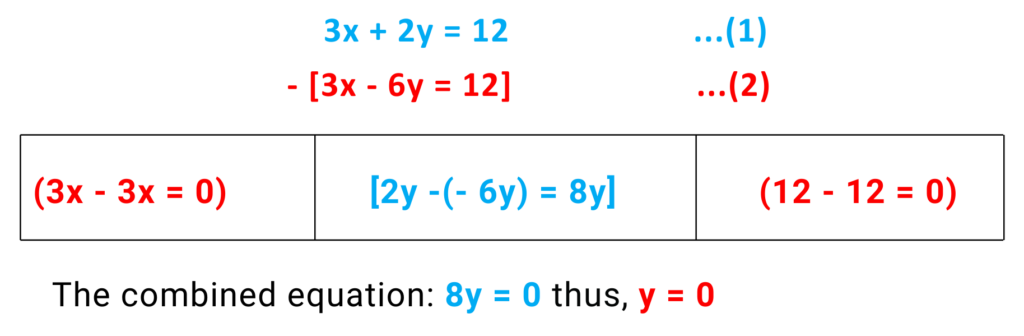
Step#3: Use the known value of one variable to find the value of the other variable –
Pick one of the original Equations and put y = 0 –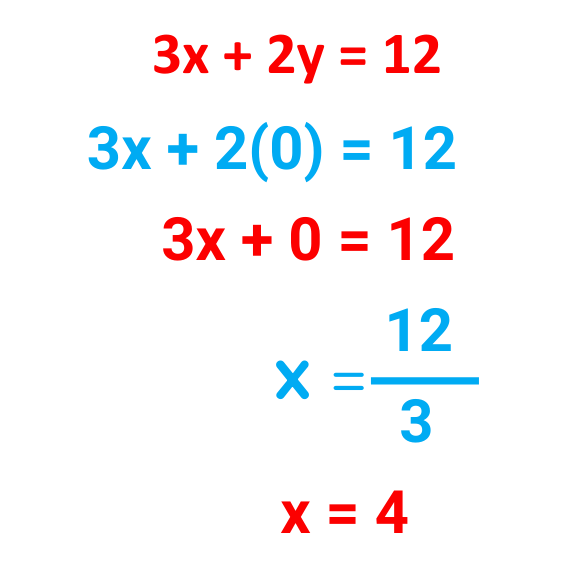
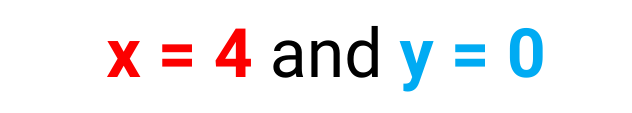
 Solved Example:
Solved Example:
Problem: Solve the following pair of Simultaneous equations by using the Substitution method.
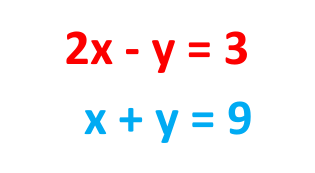
Solution:
Step#1: Find one variable’s value in the form of the other variable:
From 1st Equation-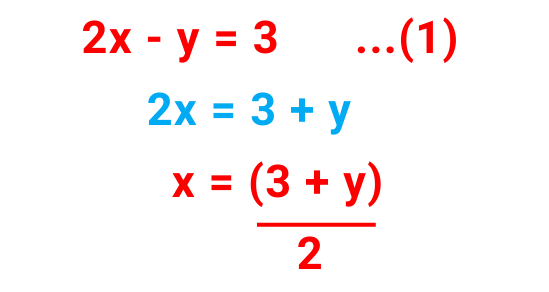
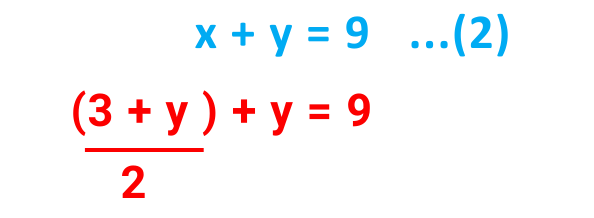
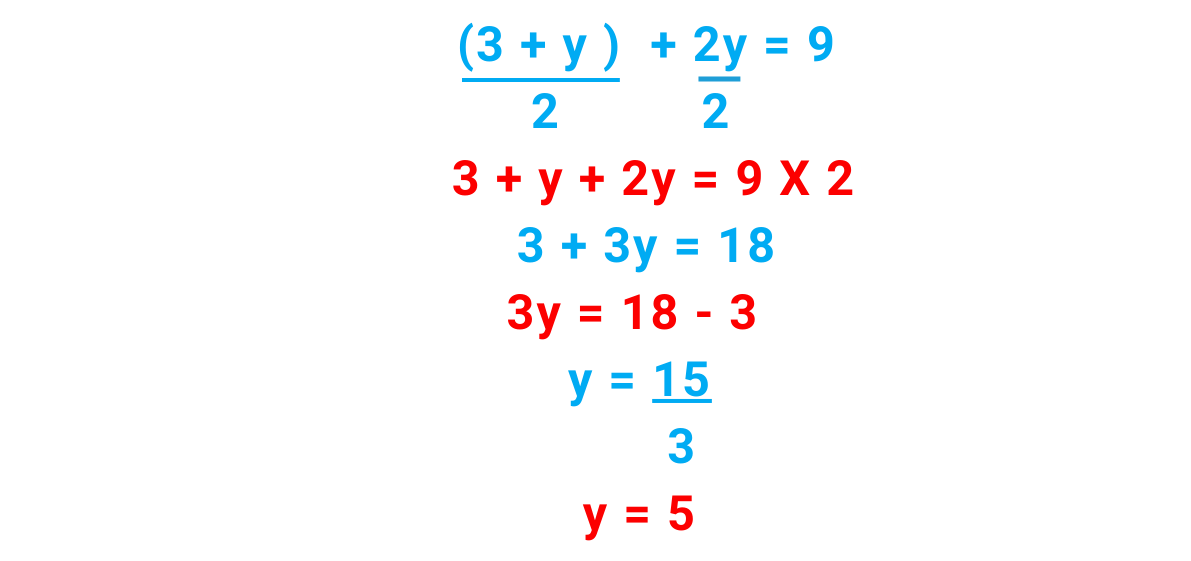
From 1st Equation: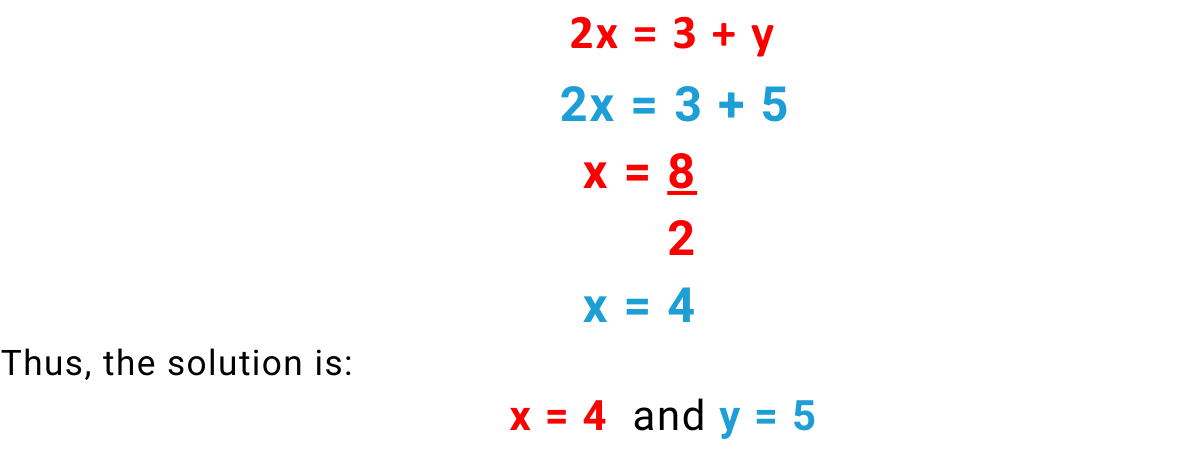
 Solved Example:
Solved Example:
Problem: Solve the following pair of Simultaneous equations by using the Elimination method.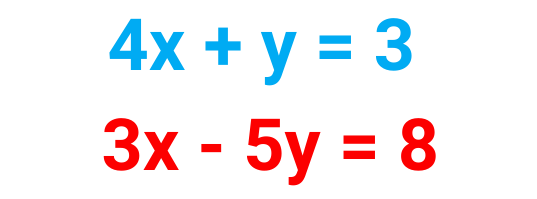
Solution:
Step#1: Identify the variable that can be eliminated :
Here, if we multiply the 1st equation with 3 and 2nd equation with 4 then the coefficient of x in both the equations will become equal –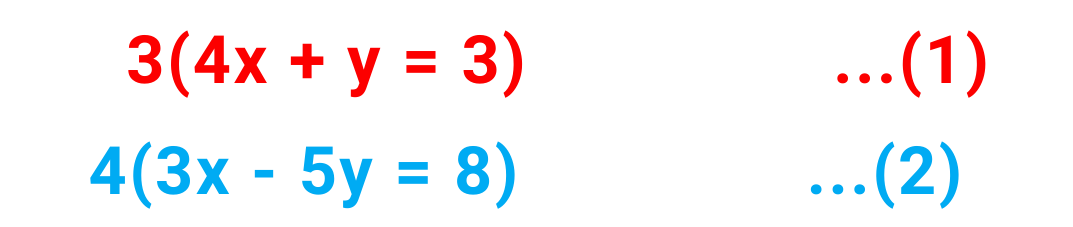
and the 1st equation becomes –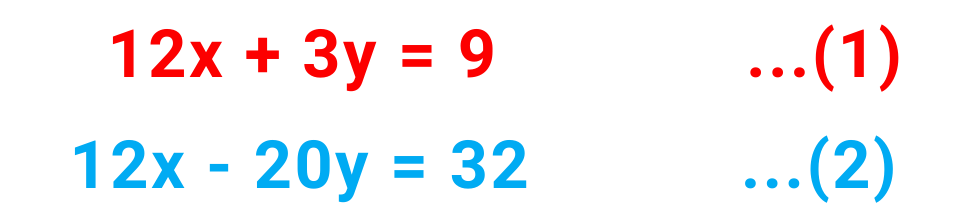
Step#2: Subtract the 2nd equation from 1st.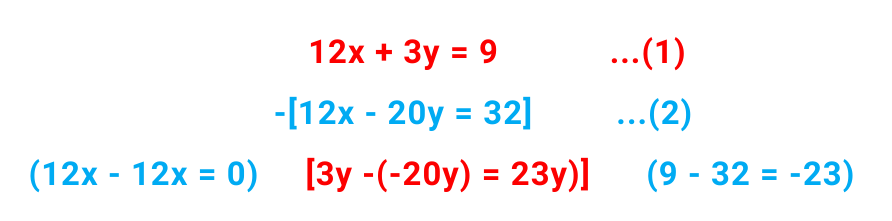
The combined equation is-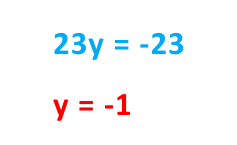
Step#3:Use the known variable’s value to find other –
From equation (1), Put y = 1 –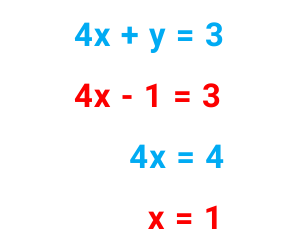
Hence the solution of these simultaneous equations are x = 1 and y = -1
Let us check whether the values satisfy the 2nd equation or not :
From 2nd equation,put x = 1 and y = -1 –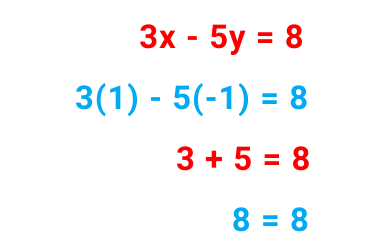
Hence, the solution is correct.

