Fractions – GCSE Maths
Introduction
- Fractions are a way to show parts of a whole. We use them when something is divided into equal pieces, and we want to talk about some of those pieces.
For Example:
- if a pizza is cut into 8 equal slices and you eat 3, you’ve eaten 3/8 of the pizza.
Types of Fractions
A fraction is a number that represents a part of a whole. It is written in the form a/b, where:
- a is the numerator – the number of parts you have.
- b is the denominator – the total number of equal parts the whole is divided into.
For Example:
- In 1/2, the whole is divided into 2 parts, and we have 1 of them.
Let us take an example:
Now let us discuss different types of fractions:
1. Unit Fractions
- A unit fraction is a fraction in which the numerator is always 1, and the denominator is some positive integer. In other words, unit fractions are of the form 1/n, where n is any natural number (1, 2, 3, …)
For Example:
2. Improper Fractions
- An improper fraction is a fraction in which the numerator (the top number) is greater than or equal to the denominator (the bottom number). In other words, the fraction represents a value that is equal to or greater than 1.
For example:
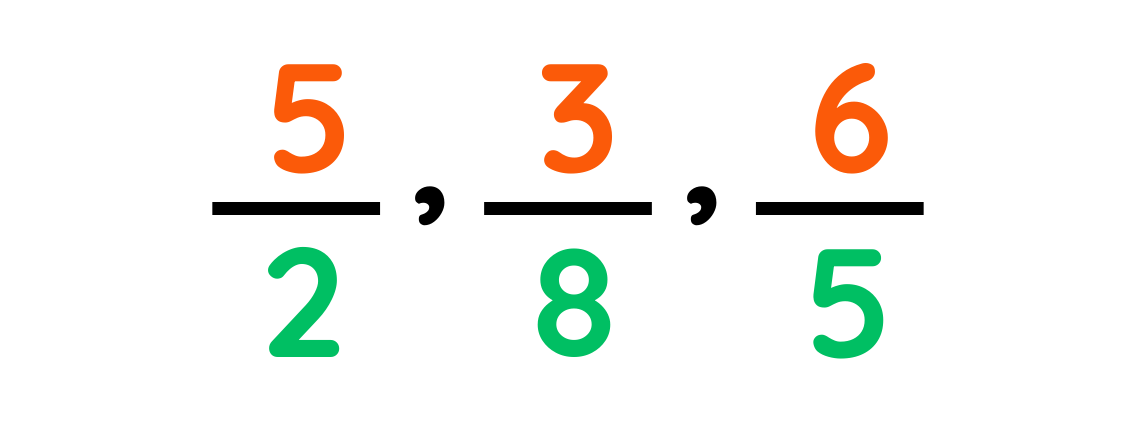
3. Mixed Numbers
- A mixed number is a combination of a whole number and a proper fraction (a fraction where the numerator is smaller than the denominator). It is used to represent quantities greater than 1 in a more intuitive way.
For example:
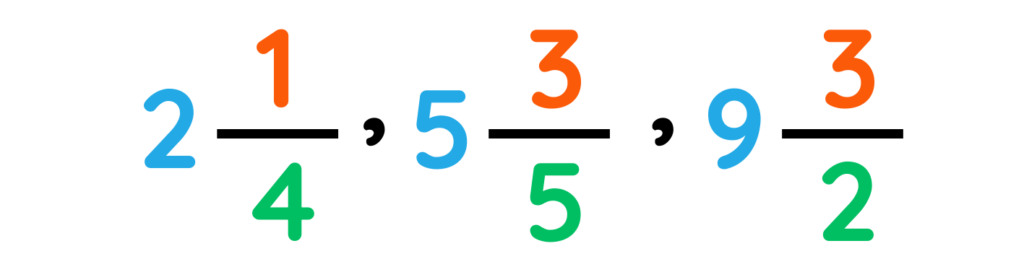
Converting into Forms
- Converting Mixed fractions to Improper fractions.
Steps to Converting Mixed fractions to Improper fractions:
- Step #1: Multiply whole number × denominator.
- Step #2: Add numerator.
- Step #3: Write over the same denominator.
Solved Example:
Solved Example: Problem: Convert 5 1/4 to an improper fraction.
Solution:
Step #1: Multiply whole number × denominator.
Step #2: Add numerator.
Step #3: Write over the same denominator.
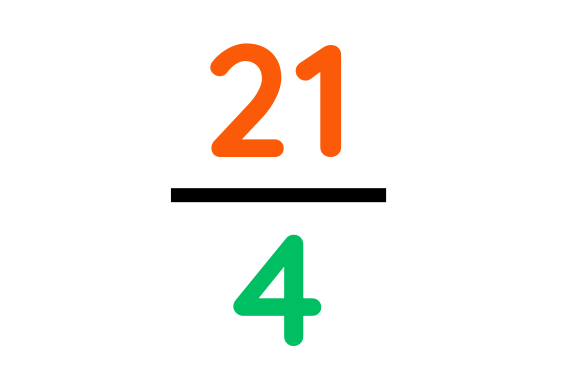
Final Answer: 21/4
Converting Decimals to Fractions
1. Terminating Decimals
- A Terminating Decimal is a decimal number that ends after a finite number of digits.
Steps:
- Step #1: Write the decimal as a fraction over 1
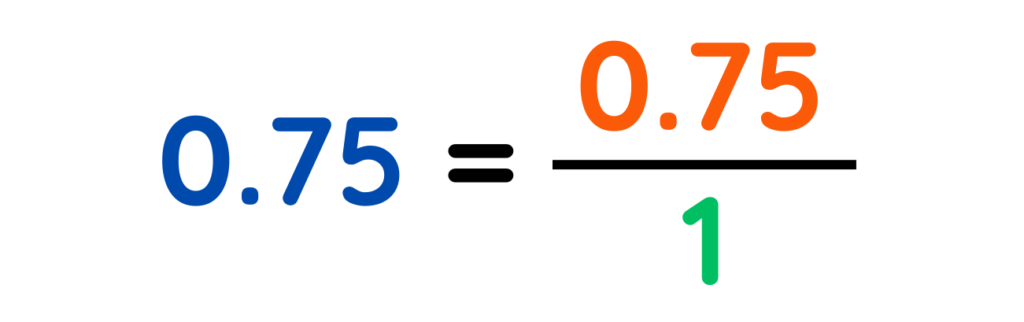
- Step #2: Multiply numerator and denominator by 10, 100, 1000, etc. to eliminate the decimal.
- Step #3: Simplify the fraction by dividing numerator and denominator by their Greatest Common Divisor (GCD).
2. Recurring Decimals
- A Recurring Decimal is a decimal number in which one or more digits repeat infinitely after the decimal point.
Let x be the repeating decimal.
Steps:
- Step #1: Multiply by 10n (where n= number of repeating digits).
- Step #2: Subtract the original equation to eliminate the repeating part.
- Step #3: Solve for x and simplify.
Solved Example:
Problem: Convert 0.125 as a fraction
Solution:
Step #1: Write the decimal as a fraction over 1
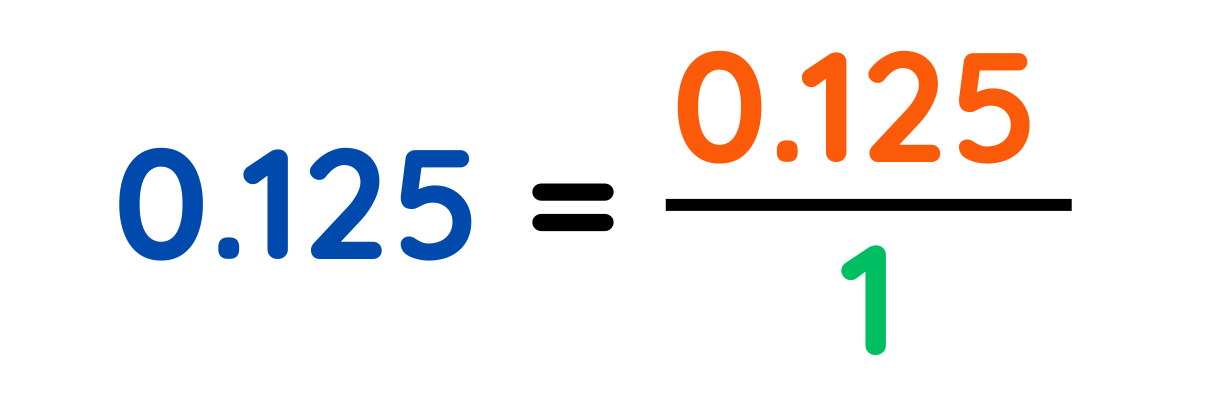
Step #2: Multiply numerator and denominator by 10, 100, 1000, etc. to eliminate the decimal.
Step #3: Simplify the fraction by dividing numerator and denominator by their Greatest Common Divisor (GCD).
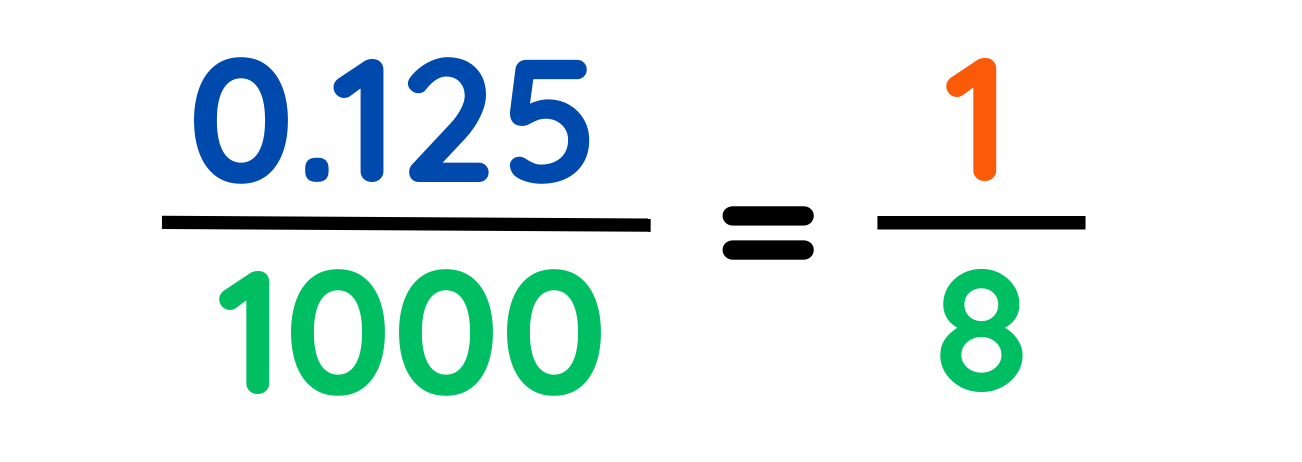
Final Answer: 1/8
Solved Example:
Problem: Convert 0.7̅ to a fraction.
Solution:
Let x = 0.7̅
Step #1: Multiply be 10 since 1 digit repeats itself
Step #2: Subtract the original equation
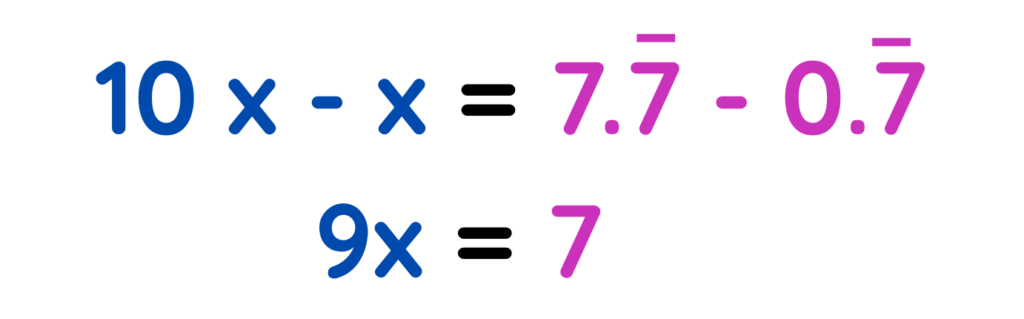
Step #3: Solve for x:
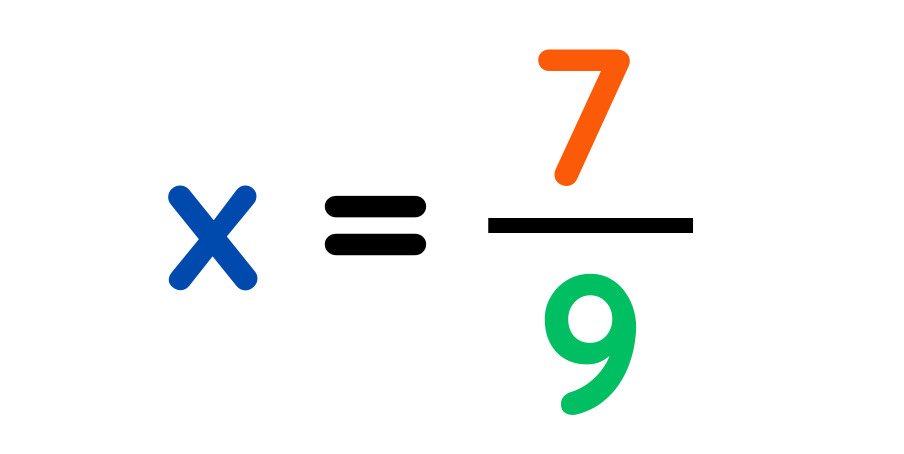
Final Answer: 7/9
Reciprocals
Reciprocal is generally the “flip” of a fraction or the multiplicative inverse that results in 1 when multiplied by the original number.
- FRACTIONS: Flip the top and bottom of the fraction as
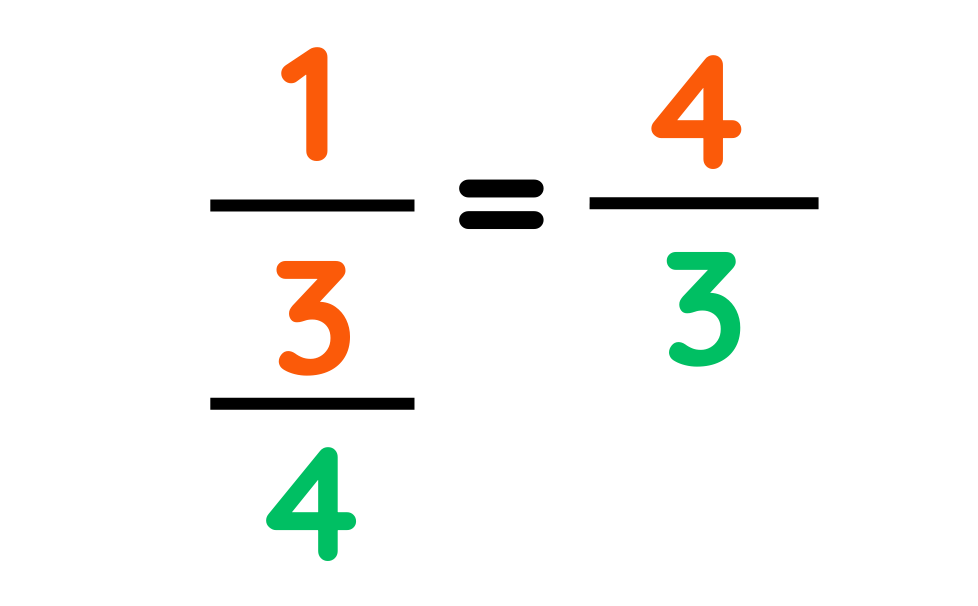
- WHOLE NUMBER: It is 1 divided by that number.
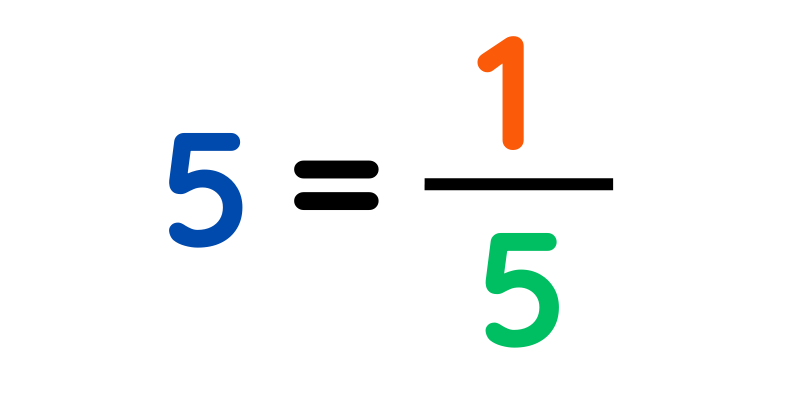
- MIXED NUMBERS: Firstly convert into improper fraction and then flip the equation
Operations with Fractions
1. Addition and Subtraction
Steps:
- Step #1: Make the bottom numbers the same
- Step #2: Add or subtract the top numbers
- Step #3: Convert back to a mixed number if needed
2. Multiplication
Steps:
- Step #1: Multiply top numbers together.
- Step #2: Multiply bottom numbers together.
- Step #3: Simplify the result.
3. Division
Steps:
- Step #1: Keep the first fraction the same.
- Step #2: Change the division sign to a multiplication sign.
- Step #3: Flip the second fraction over to write the reciprocal.
Solved Example:
Problem: Convert 3/4+ 7/2 as a fraction
Solution:
Step#1: Make the bottom numbers the same
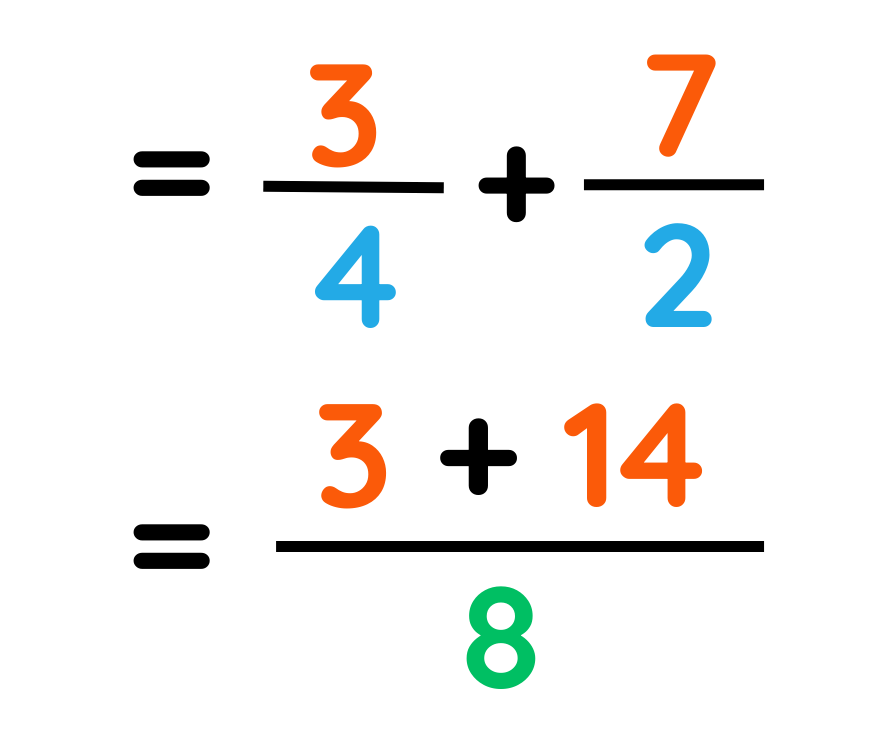
Step#2: Add the top numbers
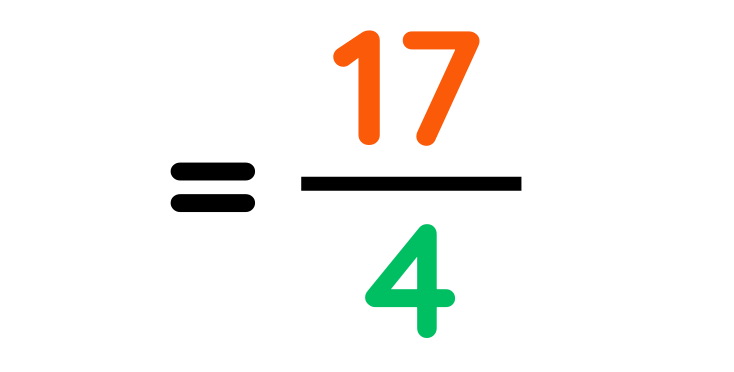
Step#3: Convert back to a Mixed Fraction
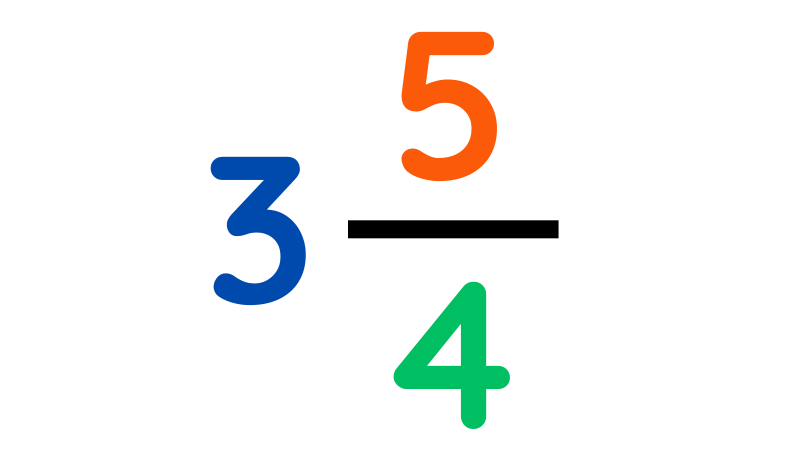
Final Answer: 3 5/4
Solved Example:
Problem: Convert 1/3 × 3/5 as a fraction
Solution:
Step#1: Multiply top numbers together.
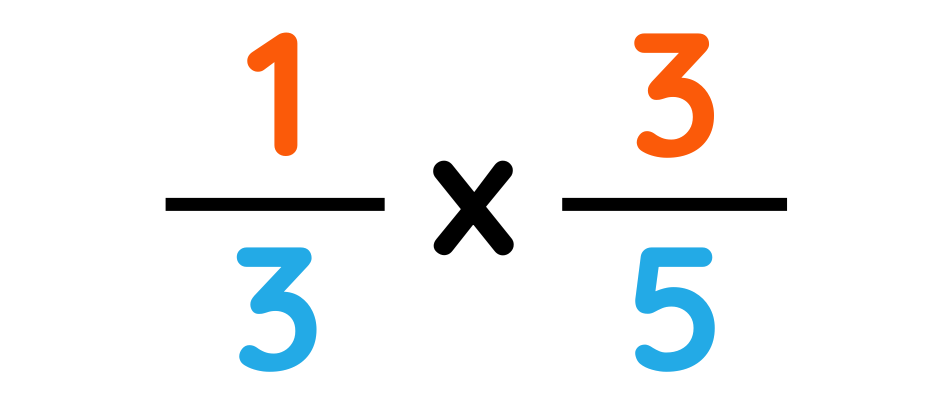
Step#2: Multiply bottom numbers together.
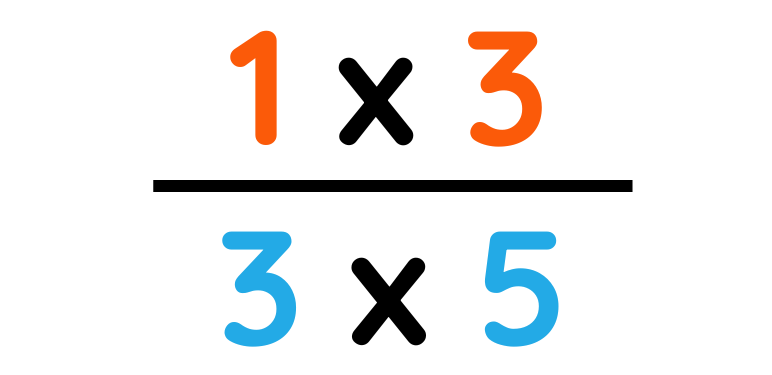
Step#3: Simplify the result
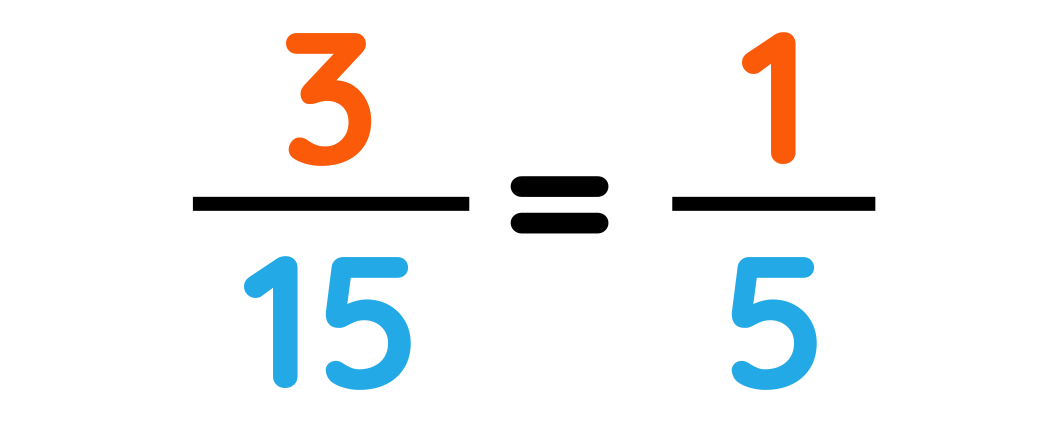
Final Answer: 1/5
Solved Example:
Problem: Convert 3/4 ÷ 7/2 as a fraction
Solution:
Step#1: Keep the first fraction same and change the divide sign to multiplication sign and reciprocate the second fraction.
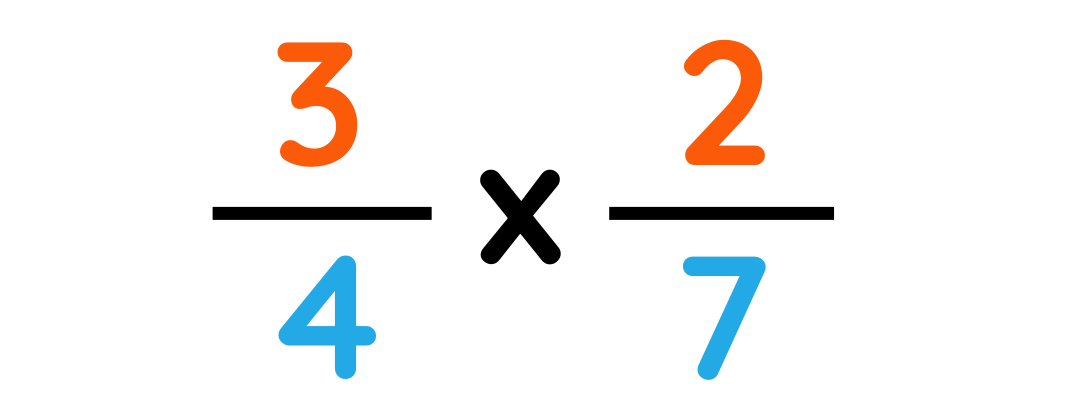
Step#2: Multiply bottom and top numbers together.
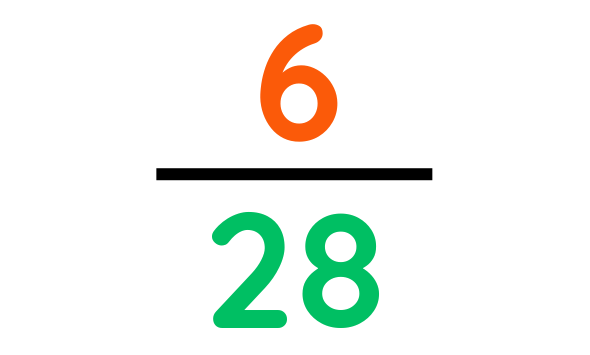
Final Answer: 6/28
Solved Example:
Problem: A builder completed 5/8 of a wall on Monday and 1/4 on Tuesday. What fraction of the wall is left to complete?
Solution:
Step#1: Write down the given information
On Monday, fraction of wall gets completed:-
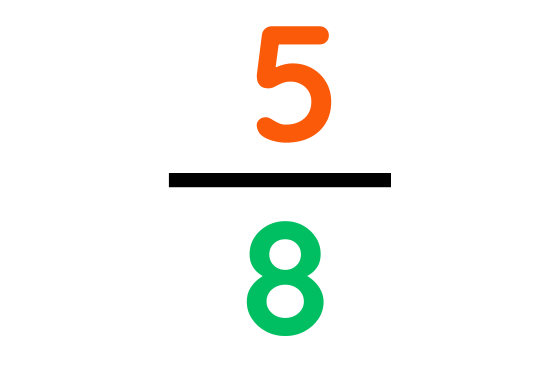
On Tuesday, fraction of wall gets completed:-
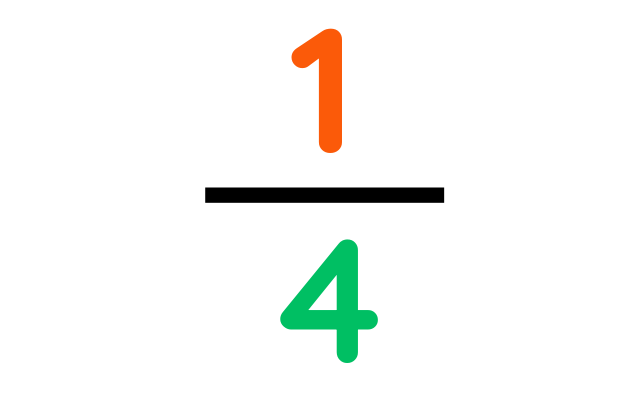
Step#2: Simplify to make a common denominator:
We know that:
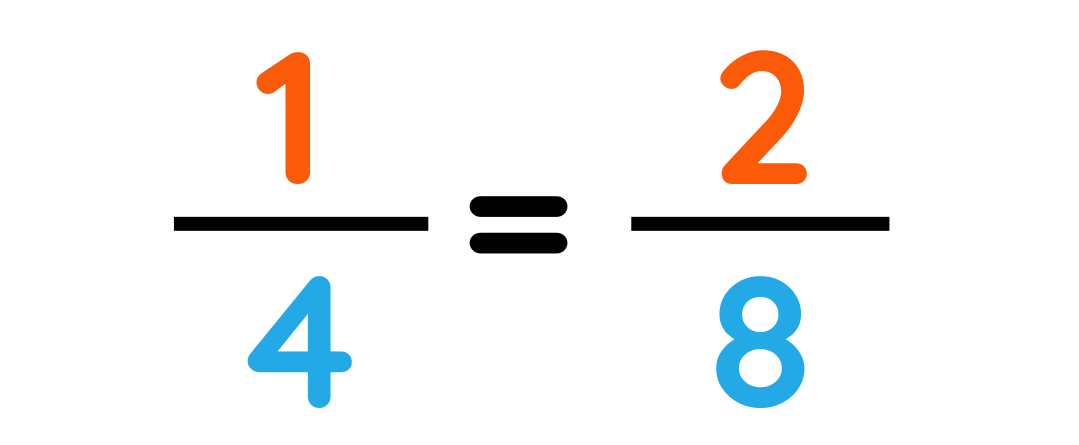
Step#3: Calculate the final result by applying favorable operations
The total amount of work that has been completed:
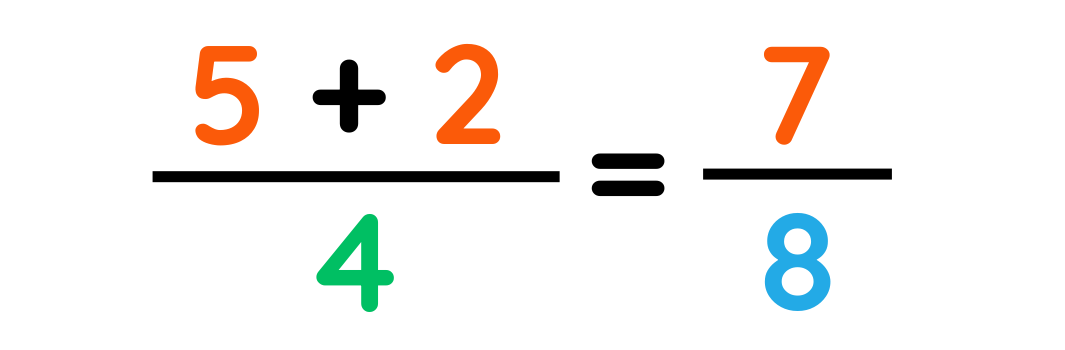
Fraction of wall that is left to complete:
Final Answer: 1/8
Solved Example:
Problem: A box has 24 pencils. 1/3 of them are red, and 1/4 are blue. How many pencils are neither red nor blue?
Solution:
Step#1: Write down the given information
Red pencils :-
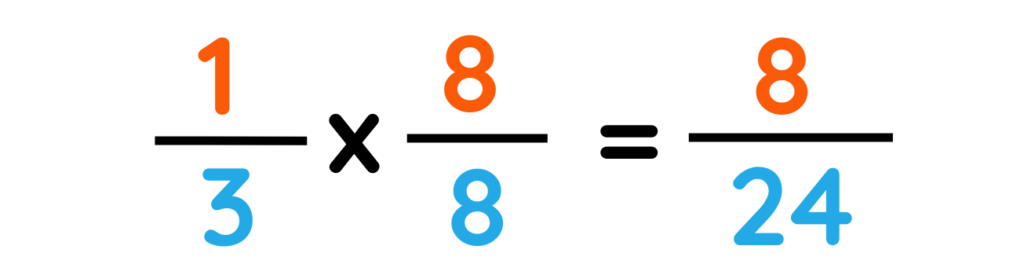
Blue pencil :-
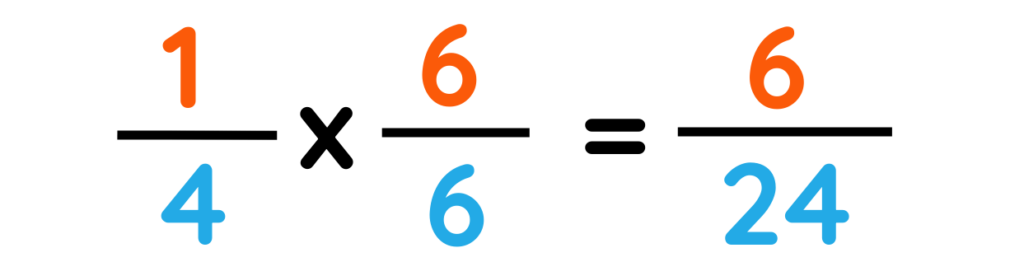
Step#2: Simplify to make a common denominator
We know that:
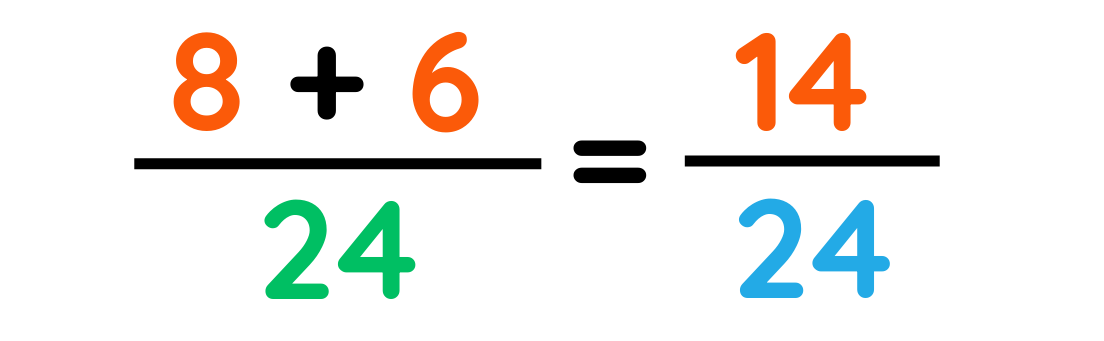
Step#3: Calculate the final result by applying favorable operations
The total number of pencils that is either red or blue :
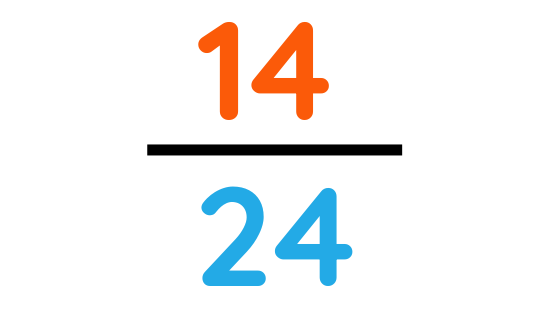
Pencils that are neither red nor blue:
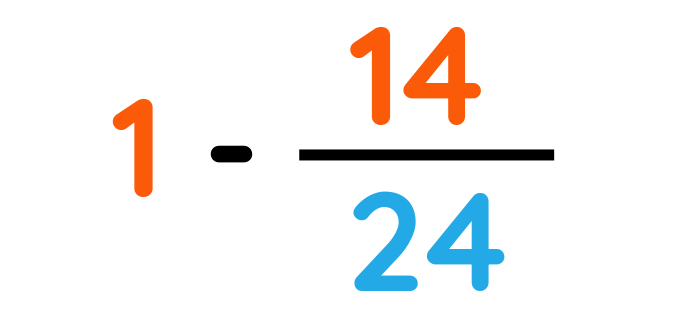
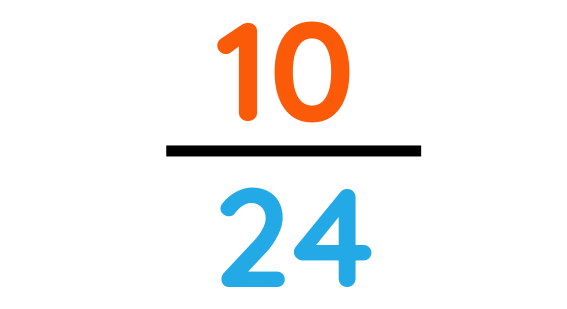
Final Answer: 10/24