How to Use SOHCAHTOA – GCSE Maths

SOHCAHTOA is used in GCSE Maths to solve problems involving right-angled triangles. It involves three basic trigonometric ratios: Sine, Cosine, and Tangent.

Practice Questions
Downloads

What is SOHCAHTOA?

  • The term “SOHCAHTOA” is an simple way to help remember the three main trigonometric ratios: Sine, Cosine and Tangent.

What are SOHCAHTOA Rules?

SOHCAHTOA helps you remember the relationship between angles and sides in a right-angled triangle. It stands for:

  • SOH:

Sine = Opposite side ÷ Hypotenuse

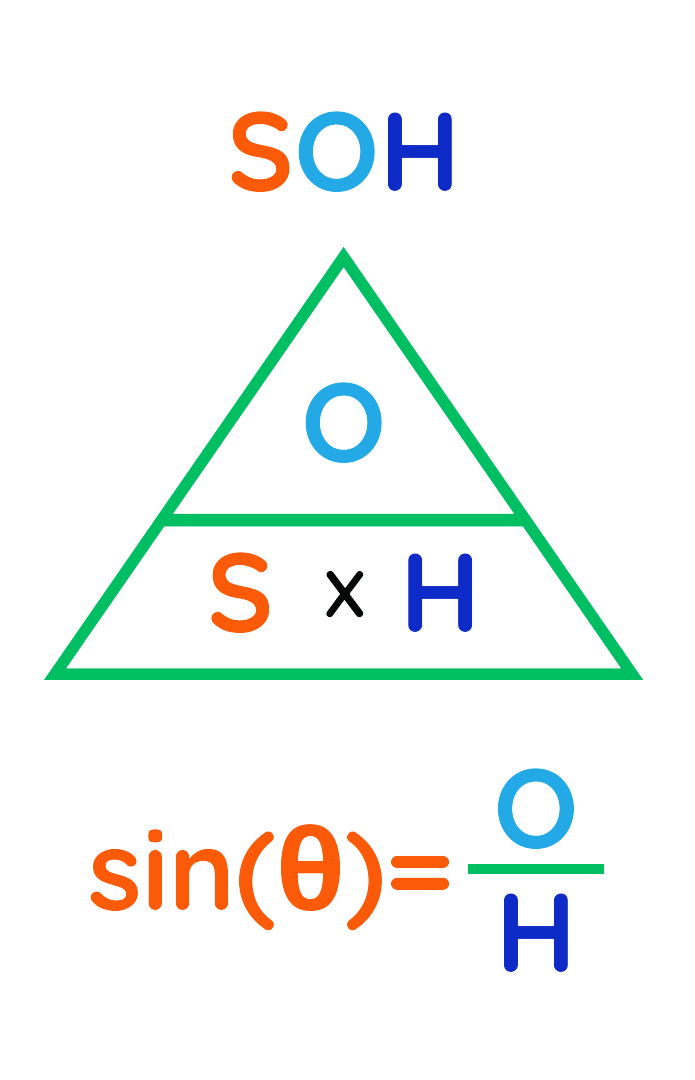
  • CAH:

Cosine = Adjacent side ÷ Hypotenuse

  • TOA:

Tangent = Opposite side ÷ Adjacent side

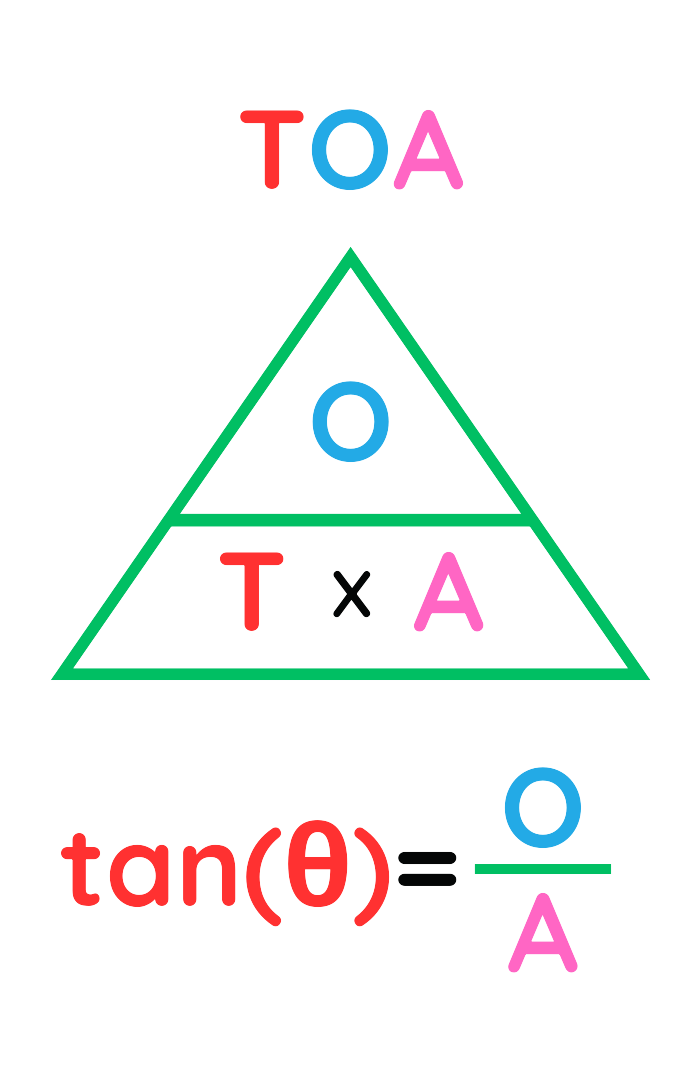
✨ Tips to Remember✨

A clearly labeled diagram of a triangle can help you better understand these relationships.

  • The side opposite the angle is called the opposite.

  • The side touching the angle is called the adjacent.

  • The largest side, opposite the right angle, is called the hypotenuse.

Does SOHCAHTOA Only Work for Right Triangles?

Yes, SOHCAHTOA only works with right angle triangle.

For other triangles, we use the Law of Sine and Cosine to find missing sides and angles.

If you want to learn more about the law of sine and cosine please click on this link: Law of sine and cosine.

How to Use SOHCAHTOA – To Find an Unknown Side of a Right Triangle

Using SOHCAHTOA involves these 3 simple steps:

Step #1: Label the Sides Clearly

  • Identify the triangle’s opposite, adjacent, and hypotenuse sides based on your reference angle.
  • Once the sides are labeled, you will have two sides identified—one is given, and the other needs to be found.

Step #2: Use the Correct Trigonometric Ratio

  • Based on the given side and the side you need to find, use the correct trigonometric ratio. For example,
  • Use Sine Theta (SOH) if you are dealing with opposite and hypotenuse.

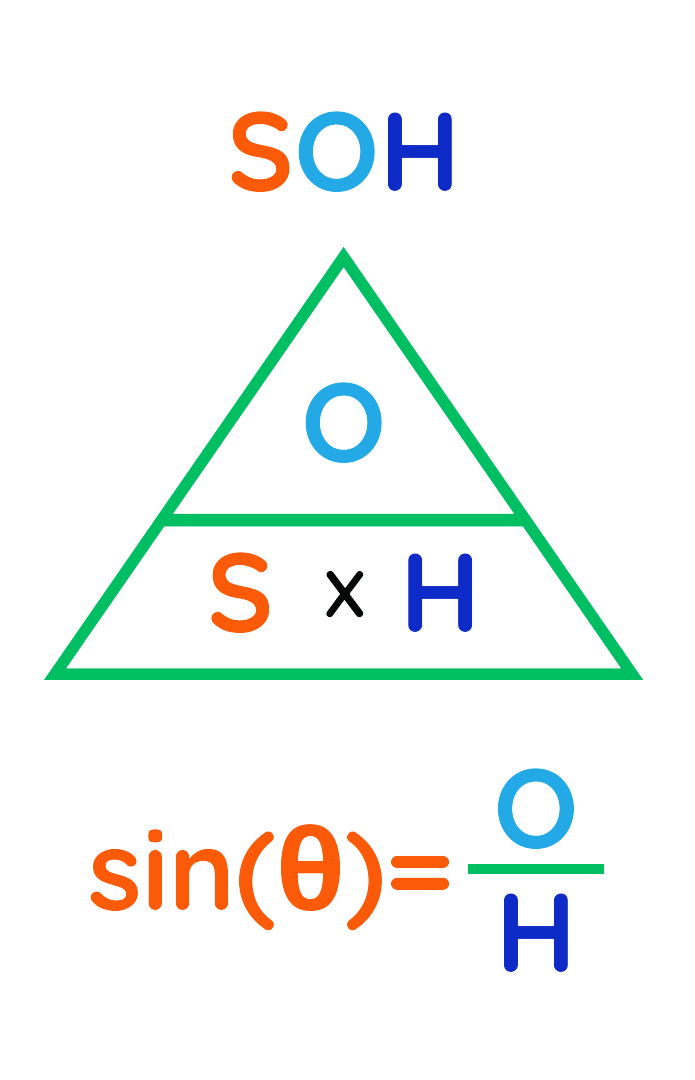
  • Use Cosine Theta (CAH) if you are dealing with adjacent and hypotenuse.

  • Use Tangent Theta (TOA) if you are dealing with opposite and adjacent sides.

Step #3: Solve the Example Briefly

  • Use the selected trigonometric formula, substitute the known values, and solve for the missing side with a quick calculation. Here’s a clear example:
  • If you know the opposite side and need the hypotenuse, use the Sine formula

certified Physics and Maths tutorSolved Example

Problem: A right-angled triangle has a hypotenuse of 10 cm and an angle of 30°. Find the length of the opposite side.

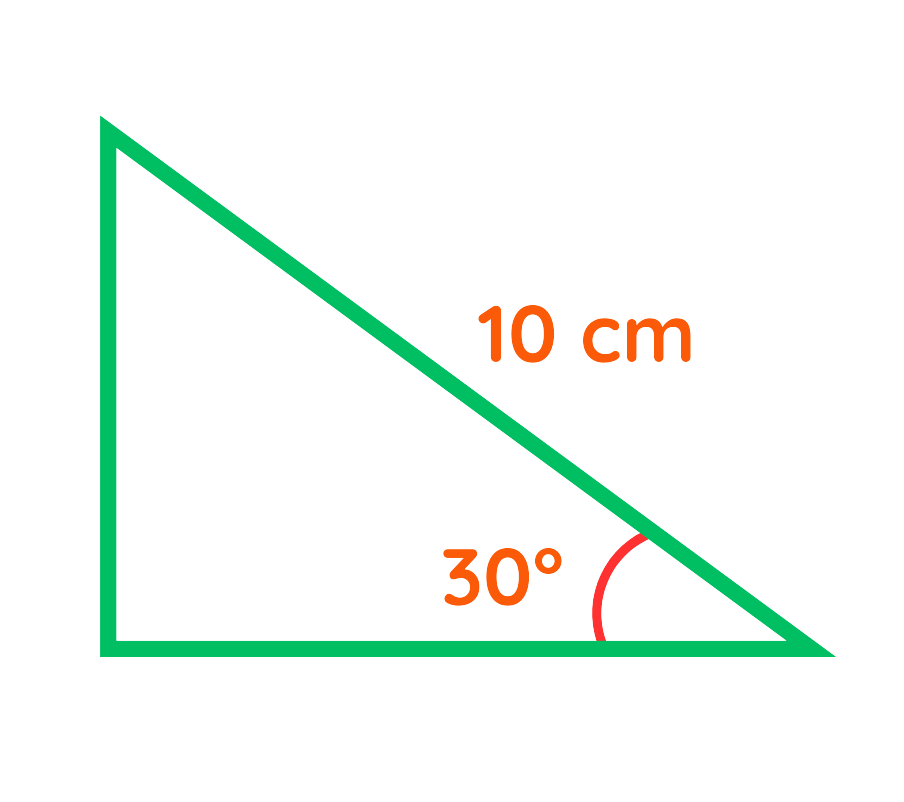
Solution: 

Step #1: Identify the given values:

    • Hypotenuse = 10 cm
    • Angle = 30°

Step #2: Choose the correct trigonometric ratio:

Since we are dealing with the opposite side and the hypotenuse, we use Sine Theta.

Step #3: Set up the equation:

Step #4: Rearrange the equation to solve for the opposite side:

Step #5: Substitute the value of sin⁡(30°) = 0.5:

Step #6: Calculate the final answer:

Thus, the length of the opposite side is 5 cm

Final Answer: 5 cm

How to Find a Missing Angle of a Right Triangle

To find a missing angle in a right-angled triangle using SOHCAHTOA, follow these 3 steps:

Step #1: Identify the Given Sides

  • Determine which two sides are provided—opposite, adjacent, or hypotenuse.
  • Label the given sides clearly.

Step #2: Use the Correct Trigonometric Ratio

  • Use Sine Theta (SOH) if you are dealing with opposite and hypotenuse.

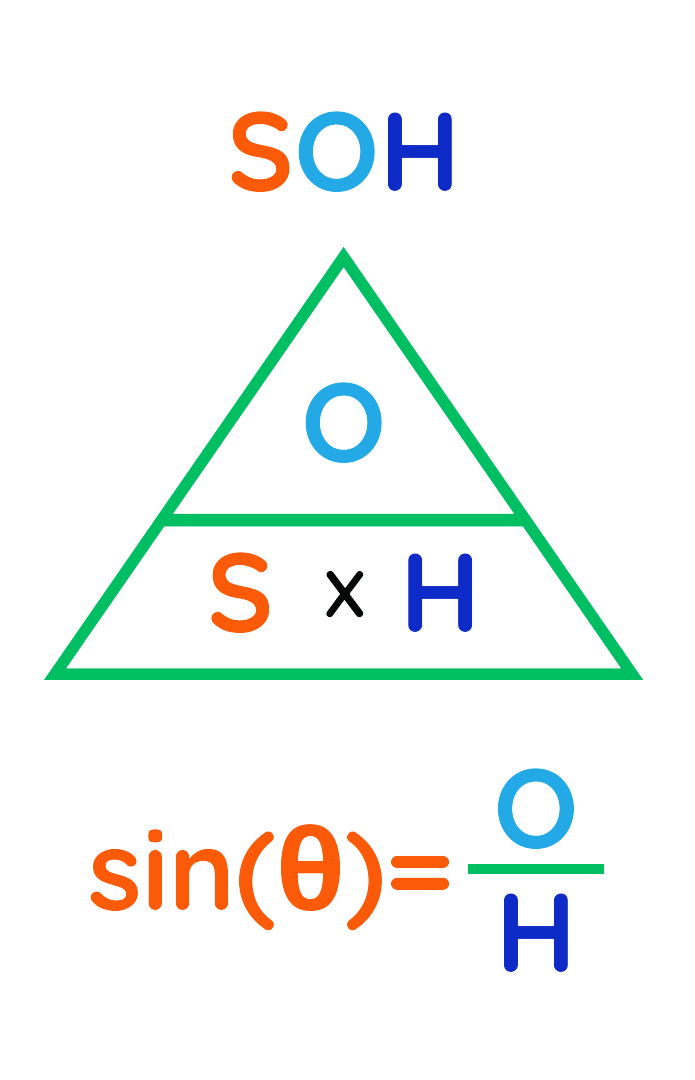
  • Use Cosine Theta (CAH) if you are dealing with adjacent and hypotenuse.

  • Use Tangent Theta (TOA) if you are dealing with opposite and adjacent sides.

Step #3: Solve for the Angle

  • Use the inverse trigonometric function (sin⁻¹, cos⁻¹, or tan⁻¹) on your calculator to find the angle.

If you want to learn more, click this link: Casio Calculator 991ex

  • Rearrange the equation if necessary.
  • Calculate to determine the missing angle.

certified Physics and Maths tutorSolved Example

Problem: A right-angled triangle has an opposite side of 4 cm and a hypotenuse of 8 cm. Find the missing angle.

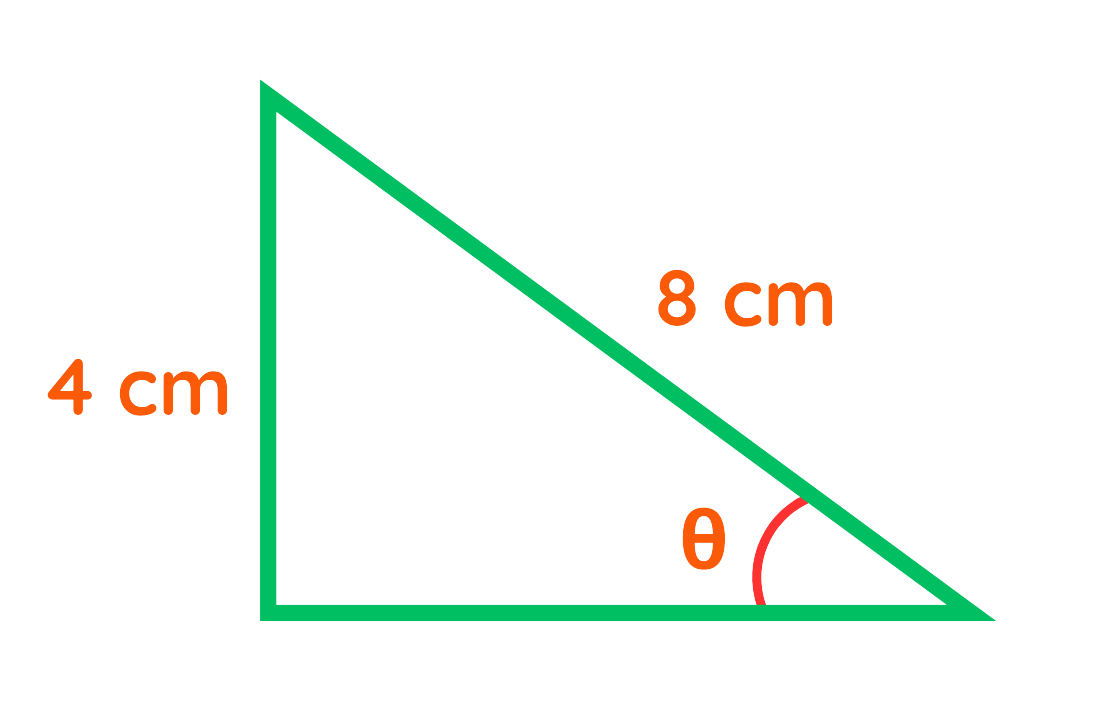
Solution: 

Step #1: Identify the given values:

    • Opposite = 4 cm
    • Hypotenuse = 8 cm

Step #2: Choose the correct trigonometric ratio:

Since we have the opposite side and the hypotenuse, we use Sine Theta.

Step #3: Set up the equation:

Step #4: Simplify the fraction:

Step #5: Use the inverse sine function to find the angle:

Step #6: Calculate the final answer:

Thus, the missing angle is 30°.

Final Answer: 30°

Three Additional Solved Examples

certified Physics and Maths tutorSolved Example 1

Problem: A right-angled triangle has an angle of 35° and a hypotenuse of 15 cm. Find the length of the opposite side.

Solution: 

Step #1: Identify the given values:

    • Hypotenuse = 15 cm
    • Angle = 35°

Step #2: Choose the correct trigonometric ratio:

Since we are dealing with the opposite side and the hypotenuse, we use Sine Theta.

Step #3: Set up the equation:

Step #4: Rearrange the equation to solve for the opposite side:

Step #5: Calculate the value:

Thus, the opposite side is 8.60 cm.

Final Answer: 8.60 cm

certified Physics and Maths tutorSolved Example 2

Problem: A right-angled triangle has an adjacent side of 5 cm and a hypotenuse of 13 cm. Find the missing angle.

Solution: 

Step #1: Identify the given values:

    • Adjacent = 5 cm
    • Hypotenuse = 13 cm

Step #2: Choose the correct trigonometric ratio:

Since we have the adjacent side and the hypotenuse, we use Cosine Theta.

Step #3: Set up the equation:

Step #4: Use the inverse cosine function:

Step #5: Calculate the value:

Thus, the missing angle is 67.38°

Final Answer: 67.38°

certified Physics and Maths tutorSolved Example 3

Problem: A ladder leans against a wall, reaching a height of 15 meters. The ladder makes an angle of 65° with the ground. Find the length of the ladder.

Solution: 

Step #1: Identify the given values:

    • Opposite side (height) = 15 m
    • Angle = 65°

Step #2: Choose the correct trigonometric ratio:

Since we have the opposite side and the hypotenuse, we use Sine Theta.

Step #3: Set up the equation:

Step #4: Rearrange the equation to solve for the hypotenuse:

Step #5: Calculate the value:

Thus, the ladder is 16.55 meters long

Final Answer: 16.55 m

Practice Questions and Answers on SOHCAHTOA

Question 1:

Two right-angled triangles are shown below.

AB is 10cm

BC is 3cm

Angle BCD is 65°

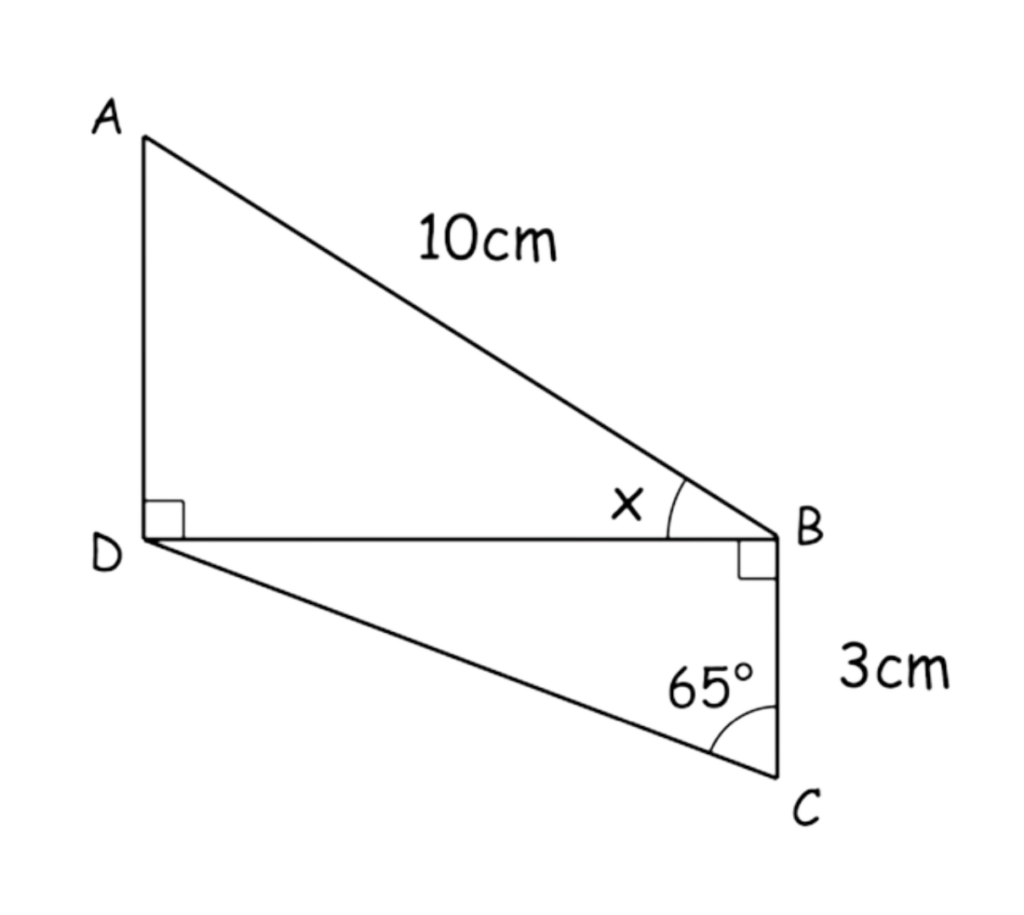
Calculate the size of angle ABD

 

Question 2:

Shown below are right-angled triangles, ABD and BCD.

AB = 15cm

Angle ABD = 70°

Angle ABD : Angle DBC = 5 : 2

Work out the length of CD

 

Question 3:

The diagram shows two right-angled triangles.

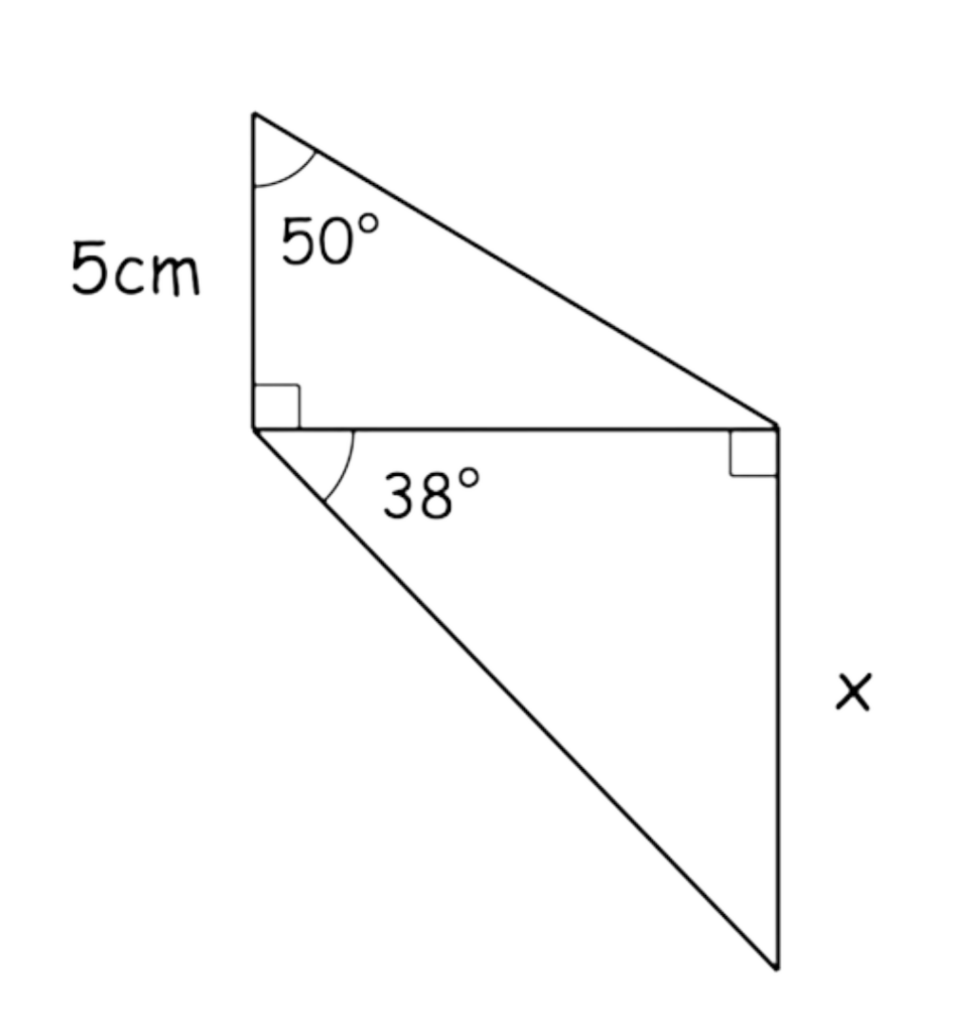
Calculate the value of x

 

Question 4:

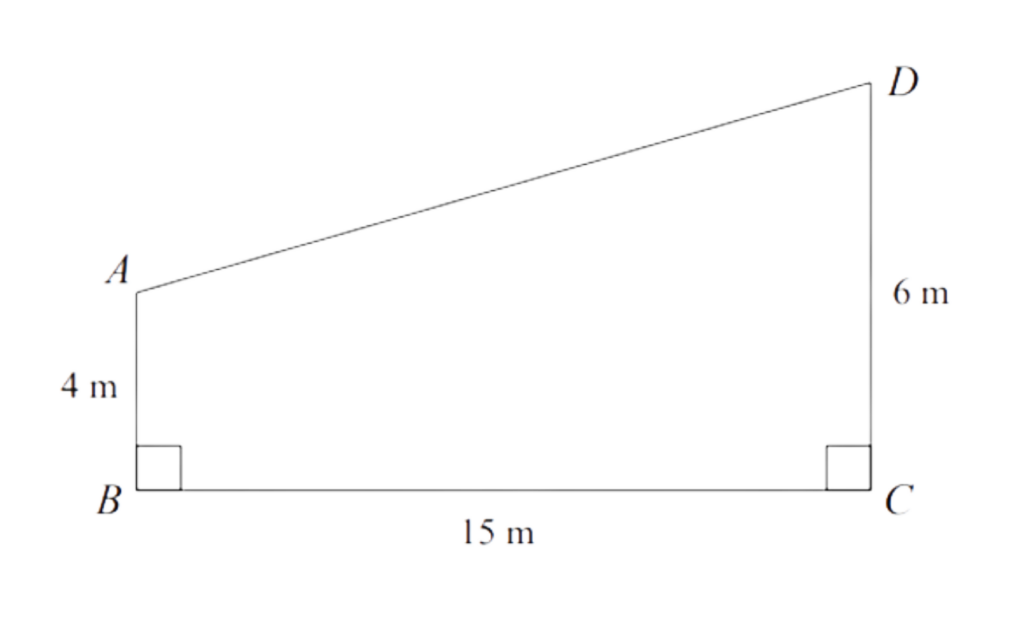
Work out the size of angle BAD.

Give your answer to 1 decimal place.

 

Question 5:

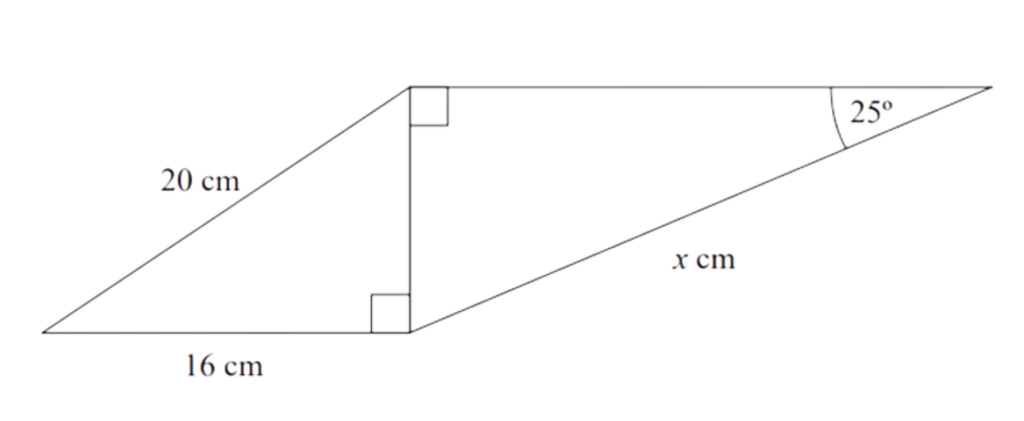
Work out the value of x.

Give your answer to 1 decimal place.

 

Question 6: 

Work out the size of angle BCD.

Give your answer to 1 decimal place.

 

Question 7: 

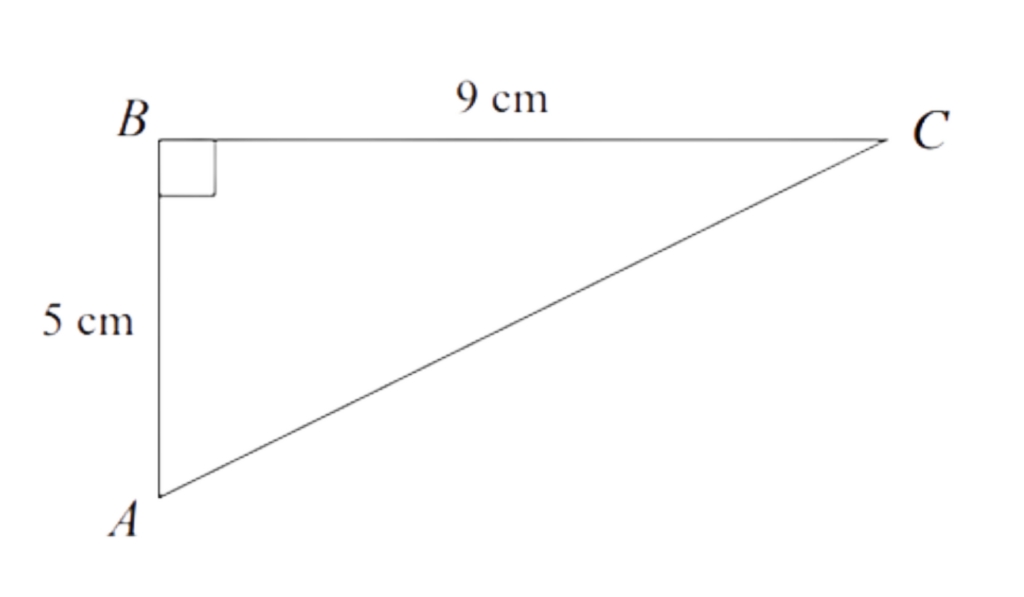
Calculate the size of angle BAC.

 

Question 8:

Calculate the size of angle ACB.

 

Question 9: 

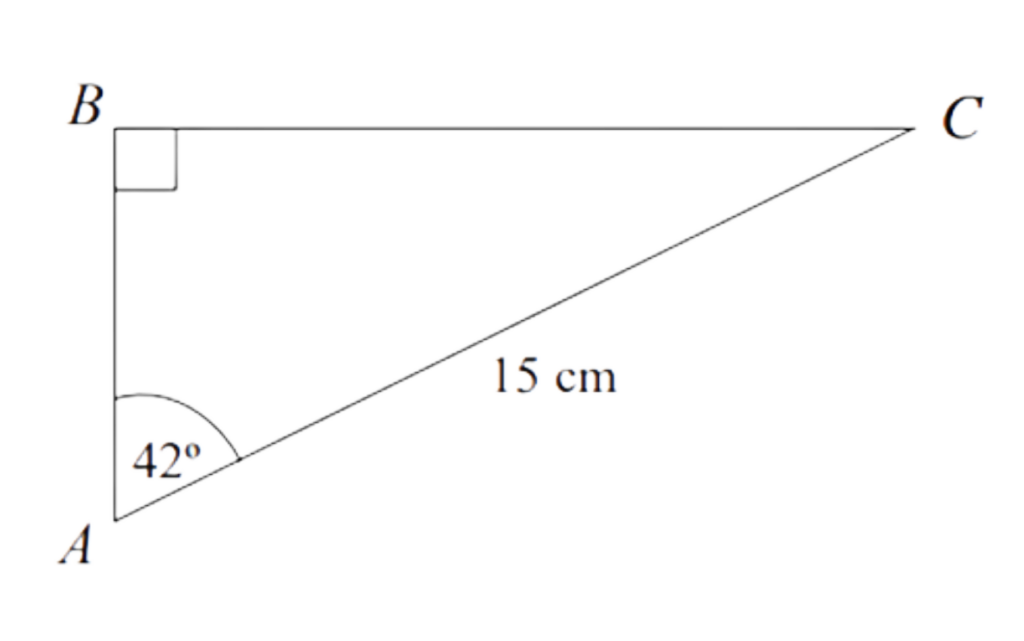
Calculate the length AB.

 

Question 10: 

Triangle ABC has a right angle.

Angle BAC is 25°

AC = 12.5cm

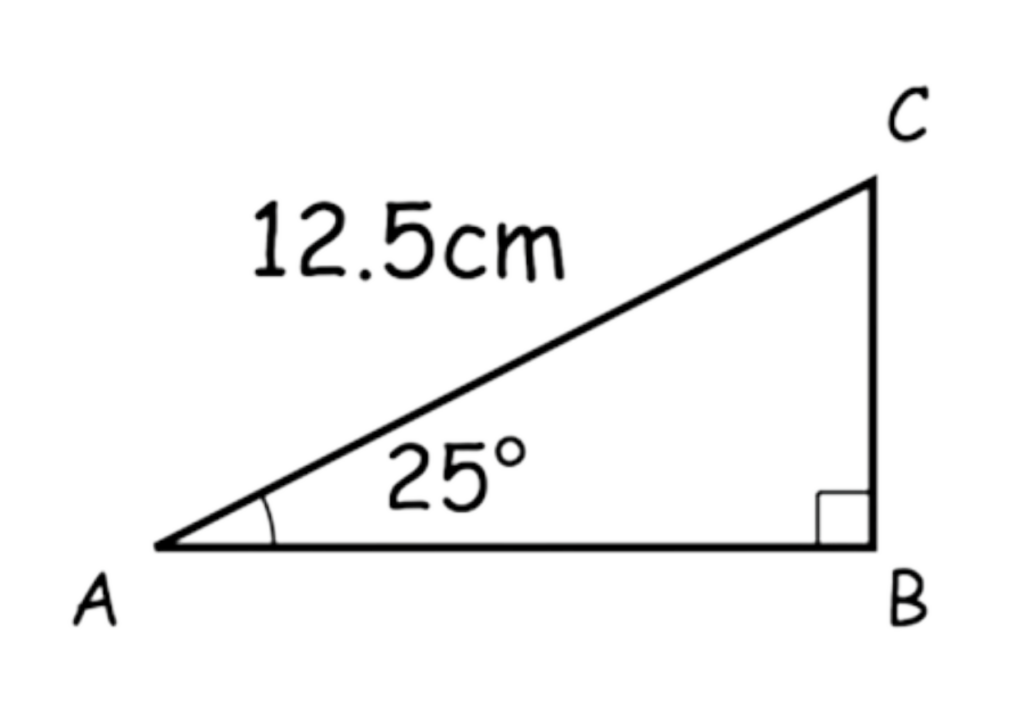
Calculate the length of AB

Solutions

Question 1: 

Solution: 

Step #1: Identify the given values

AB = 10 cm (hypotenuse)

BC = 3 cm (adjacent to angle BCD)

Angle BCD = 65°

Find angle ABD

Step #2: Find BD (opposite side in triangle ABD) using tan function

tan(65°) = BD / BC

Rearranging: BD = tan(65°) × 3

BD = 6.433 cm

Step #3: Use cosine to find angle ABD

cos(ABD) = BD / AB

cos(ABD) = 6.433 / 10

cos(ABD) = 0.6433

Step #4: Find ABD using inverse cosine

ABD = cos⁻¹(0.6433)

ABD ≈ 49.69°

Step #5: Final Answer: Angle ABD = 49.69°

 

Question 2:

Solution: 

Step #1: Identify the given values

AB = 15 cm

Angle ABD = 70°

Angle ratio ABD : DBC = 5 : 2

Find CD

Step #2: Find Angle DBC

Let Angle DBC = x

Since ABD : DBC = 5 : 2, we set up:

5x + 2x = 70°

7x = 70

x = 10°

Angle DBC = 10°

Step #3: Use the sine function to find CD

sin(10°) = CD / 15

Rearranging: CD = 15 × sin(10°)

CD ≈ 15 × 0.1736

CD ≈ 2.73 cm

Step #4: Final Answer: CD = 2.73 cm

 

Question 3:

Solution: 

Step #1: Use the Pythagorean theorem if two sides are known:

x² = hypotenuse² – one side²

Step #2: If an angle and one side are given, use SOHCAHTOA:

sin(angle) = opposite / hypotenuse

cos(angle) = adjacent / hypotenuse

tan(angle) = opposite / adjacent

Step #3: Rearrange the equation to solve for x.

Step #4: Substitute the given values and calculate:

x = 4.66 cm

Step #5: Final Answer: Angle x = 4.66 cm

 

Question 4:

Solution: 

Step #1: Use the correct trigonometric function based on the given sides:

sin(angle) = opposite / hypotenuse

cos(angle) = adjacent / hypotenuse

tan(angle) = opposite / adjacent

Step #2: Rearrange to solve for the angle:

angle = sin⁻¹(opposite / hypotenuse)

angle = cos⁻¹(adjacent / hypotenuse)

angle = tan⁻¹(opposite / adjacent)

Step #3: Substitute the given values and calculate:

angle BAD = 97.6°

Step #4: Final answer: Angle BAD = 97.6°

 

Question 5: 

Solution: 

Step #1: Use the tangent function:

tan(angle) = opposite / adjacent

Step #2: Rearrange to solve for x:

x = adjacent × tan(angle)

Step #3: Substitute the given values and calculate:

x = 28.4

Step #4: Final Answer: x = 28.4

 

Question 6: 

Solution: 

Step #1: Use the tangent function:

tan(angle) = opposite / adjacent

Step #2: Rearrange to solve for the angle:

angle = tan⁻¹(opposite / adjacent)

Step #3: Substitute the given values and calculate:

angle BCD = 41.8°

Step #4: Final Answer: angle BCD = 41.8°

 

Question 7: 

Solution: 

Step #1: Use the sine function:

sin(angle) = opposite / hypotenuse

Step #2: Rearrange to solve for the angle:

angle = sin⁻¹(opposite / hypotenuse)

Step #3: Substitute the given values and calculate:

angle BAC = 60.9°

Step #4: Final Answer: Angle BAC = 60.9°

 

Question 8: 

Solution: 

Step #1: Use the cosine function:

cos(angle) = adjacent / hypotenuse

Step #2: Rearrange to solve for the angle:

angle = cos⁻¹(adjacent / hypotenuse)

Step #3: Substitute the given values and calculate:

angle ACB = 18.2°

Step #4: Final Answer: Angle ACB = 18.2°

 

Question 9: 

Solution:

Step #1: Use the cosine function:

cos(angle) = adjacent / hypotenuse

Step #2: Rearrange to solve for AB:

AB = adjacent / cos(angle)

Step #3: Substitute the given values and calculate:

AB = 11.1 cm

Step #4: Final Answer: AB = 11.1 cm

 

Question 10: 

Solution: 

Step #1: Identify the given values

Hypotenuse = 12.5 cm

Angle = 25°

Find AB (adjacent side).

Step #2: Choose the correct trigonometric function

    • Since we have the adjacent side and hypotenuse, use cosine.
    • cos(angle) = adjacent / hypotenuse

Step #3: Set up the equation

cos(25°) = AB / 12.5

Step #4: Solve for AB

AB = 12.5 × cos(25°)

Step #5: Use a calculator

cos(25°) ≈ 0.9063

AB ≈ 12.5 × 0.9063

AB ≈ 11.33 cm

Step #6: Final Answer: AB = 11.33 cm

Table of Content

Join Tutoring