Venn Diagram​ – GCSE Maths

Practice Questions
Downloads

Introduction

  • A Venn diagram is a simple method to compare and group items using overlapping circles.
  • It is fundamental tool in mathematics, logic, and problem-solving.
  • Venn diagrams make complex data simple by showing it visually.

What is Venn Diagram?

  • A Venn diagram is a visual way to show relationships between different sets.
  • It uses circles to represent sets, and the overlapping areas show what the sets have in common.

Example

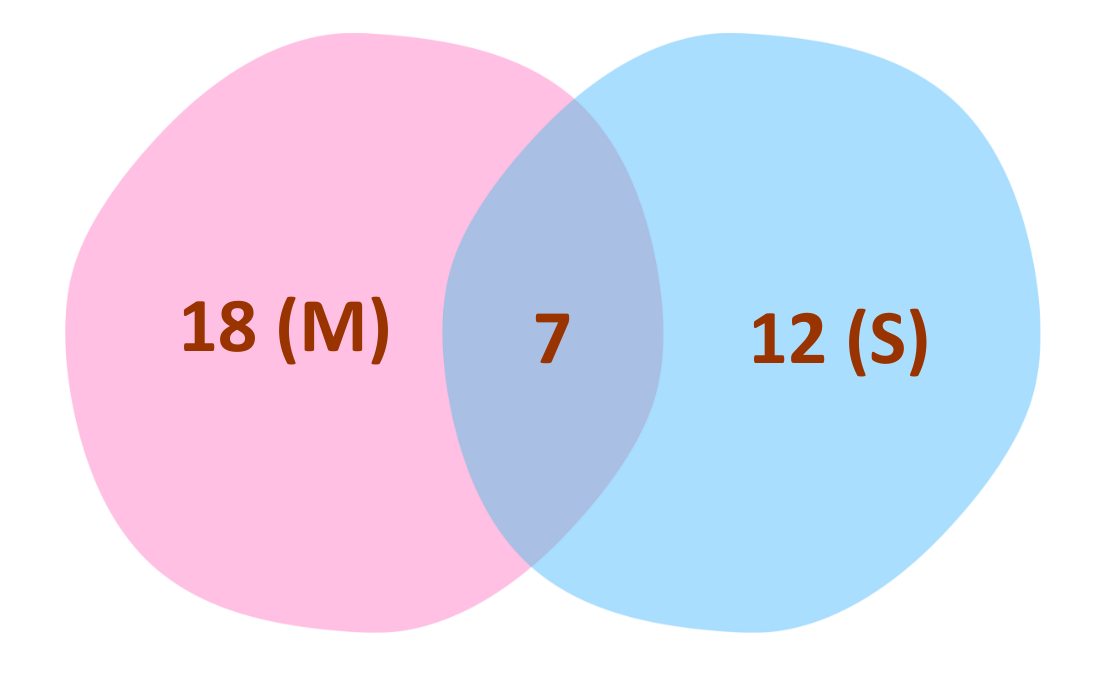
Suppose in a class of 30 students:

    • 18 like Math (M)
    • 12 like Science (S)
    • 7 like both Math and Science

Venn Diagram example showing sets M and S with 18 in M only, 12 in S only and 7 in the intersection

Set Operations in Venn Diagrams

Venn diagrams visually represent different set operations.

  • Curly brackets { } show a set of values.
  • ∈ means ‘is an element of’.

Common Set Operations in Venn Diagrams:

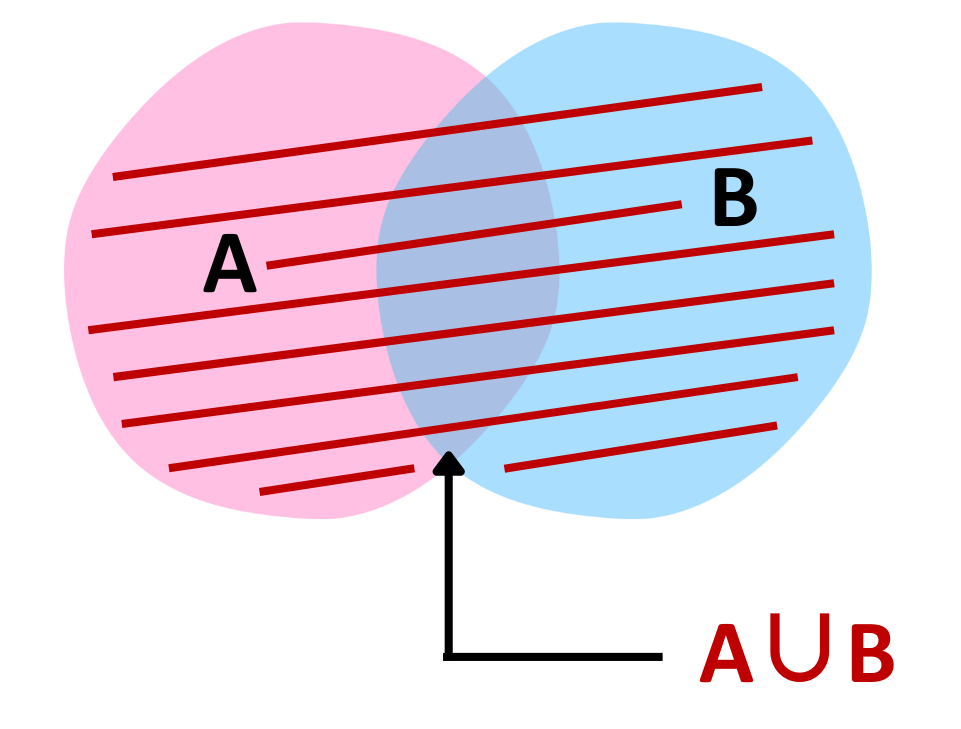
Union of Set:

  • The Union of set represents that all elements that belong to either A or B or both.

Venn Diagram showing the union of sets A and B with both circles shaded representing A union B

where,

Venn Diagram union definition formula n A union B and set notation showing elements belonging to set A or set B

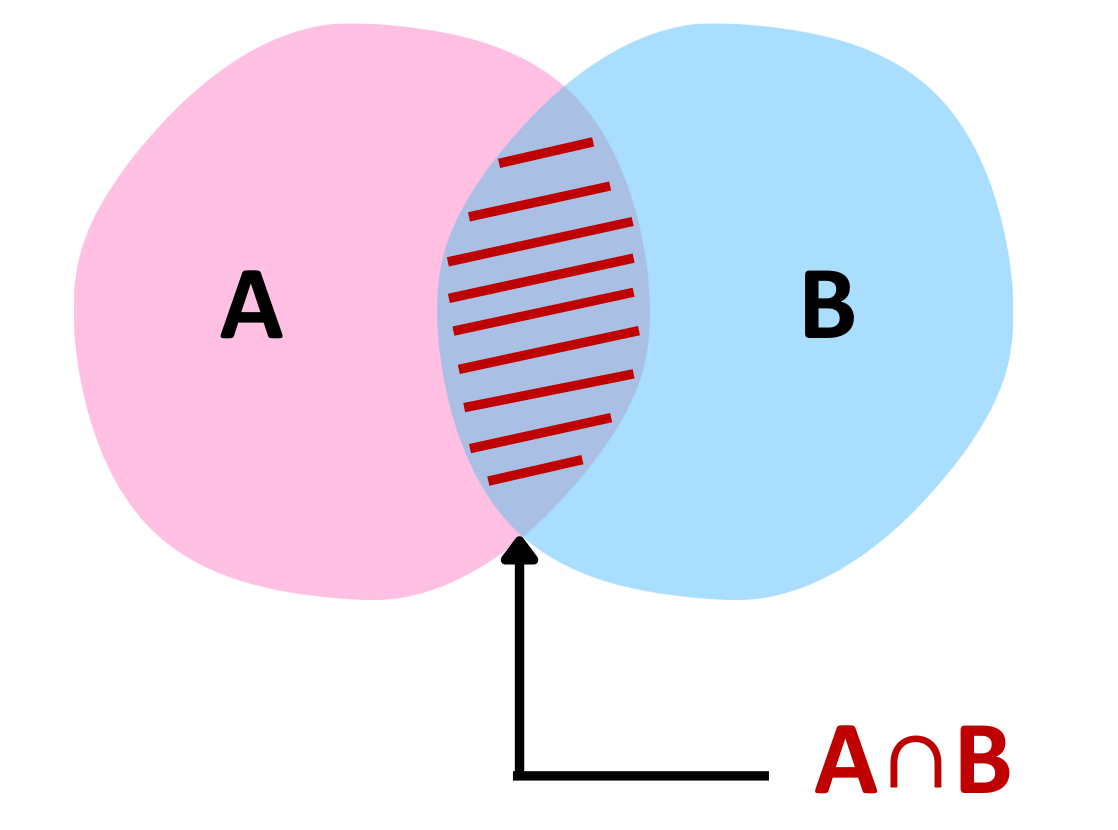
Intersection of Set:

  • The Intersection of set represents that only elements that belong to both A and B.

Venn Diagram showing the intersection of sets A and B with only the overlapping region shaded representing A intersect B

where,

Venn Diagram intersection definition formula n A intersect B and set notation showing elements belonging to both sets A and B

Compliment of a Set:

  • The Compliment of a set represents that all elements not in set A, but in the universal set.

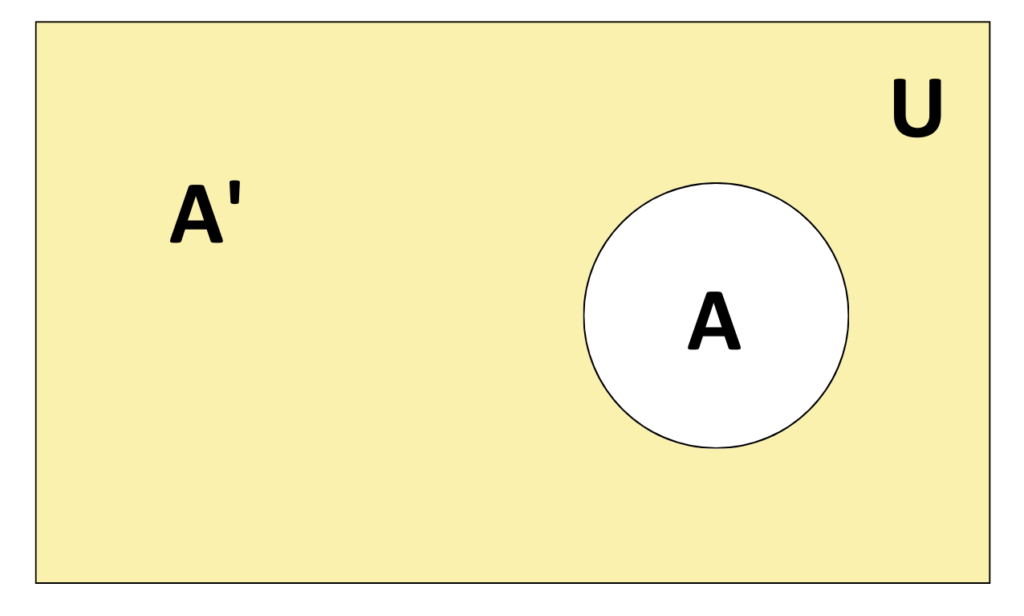
Venn Diagram showing the complement of set A, labelled A prime, outside circle A within the universal set U

where,

Venn Diagram complement formula showing n A prime and n A representing total elements inside the universal set

Difference of Set:

  • The Difference of set represents that elements in A but not in B or elements in B but not in A.

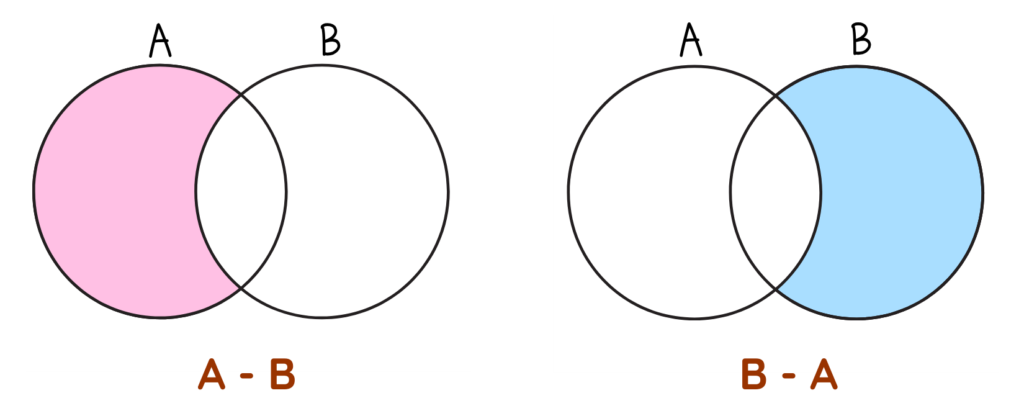
Venn Diagram showing the difference of sets A minus B and B minus A with separate shading in each circle

where,

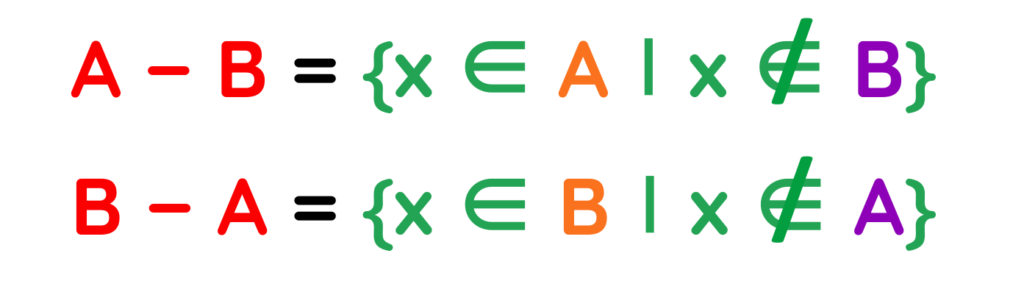
Venn Diagram set difference definition showing A minus B and B minus A using set notation

How to Calculate Probability Using Venn Diagram?

  • Probability can be visualized and calculated using Venn diagrams with the help of common set operations:

Venn Diagram set operations summary table showing union intersection difference and complement with symbols and meanings

Steps to Calculate Probability Using a Venn Diagram

  • Step #1: Define the Sample Space
  • Step #2: Define the Events
  • Step #3: Draw the Venn Diagram
  • Step #4: Calculate the Probabilities

certified Physics and Maths tutorSolved Example:

Problem: Roll a fair 6-sided die. Define two events

  • Event A: Roll an even number
  • Event B: Roll a number > 3

Find the Probability of P(A) and P(A and B).

Solution: 

Step #1: Define the Sample Space

All possible outcomes:

S = {1,2,3,4,5,6}

    • Total outcomes = 6

Step #2: Define the Events

    • Event A: {2, 4, 6}
    • Event B: {4, 5, 6}

Step #3: Draw the Venn Diagram

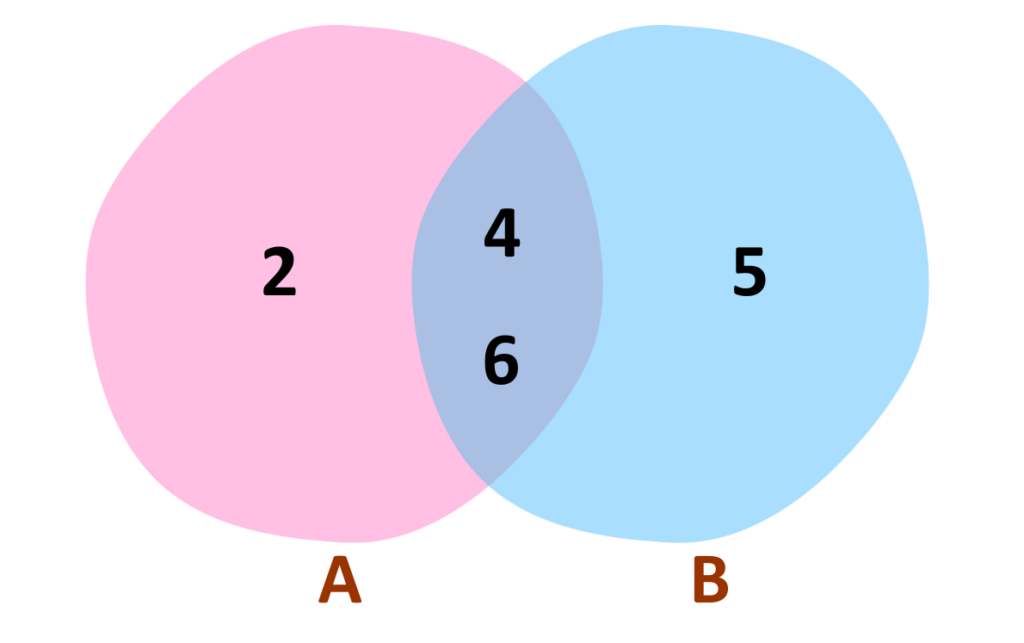
Venn Diagram example with numbers showing sets A and B with 2 in A only, 5 in B only, and 4 and 6 in the intersection

Step #4: Calculate the Probabilities

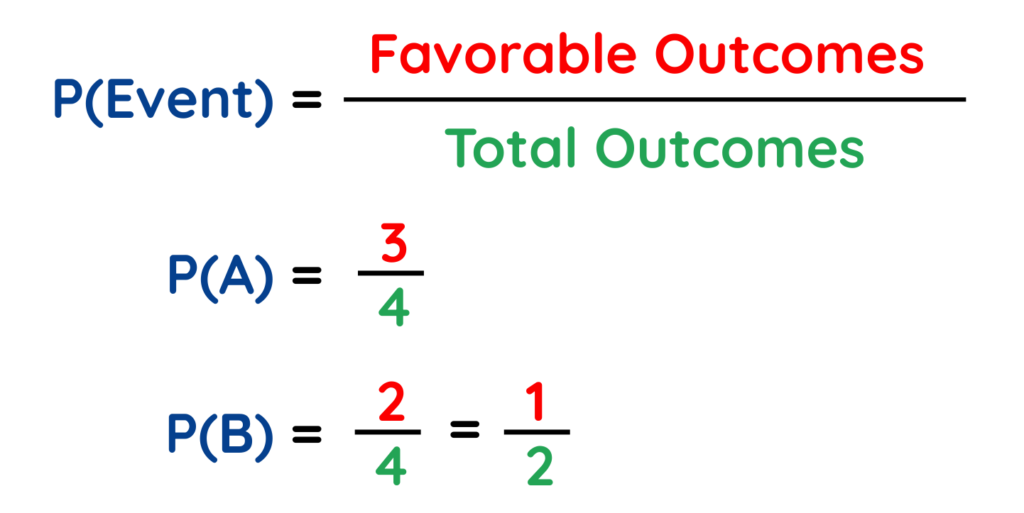
Probability of an event,

Venn Diagram probability example showing formula P event equals favorable outcomes over total outcomes with examples P A and P A and B

certified Physics and Maths tutorSolved Example:

Problem: Draw 1 card from a standard 52-card deck. Define two events:

  • Event H: Draw a Heart(♥)
  • Event K: Draw a King (♠K, ♥K, ♦K, ♣K)

Find the Probability of P(H), P(K) and P(not H).

Solution: 

Step #1: Define the Sample Space

All possible outcomes:

    • Total cards = 52
    • Hearts = 13
    • Kings = 4

Step #2: Define the Events

    • Event H = 13 cards
    • Event K = 4 cards
    • H ∩ K (King of Hearts) = 1 card (♥K)

Step #3: Draw the Venn Diagram

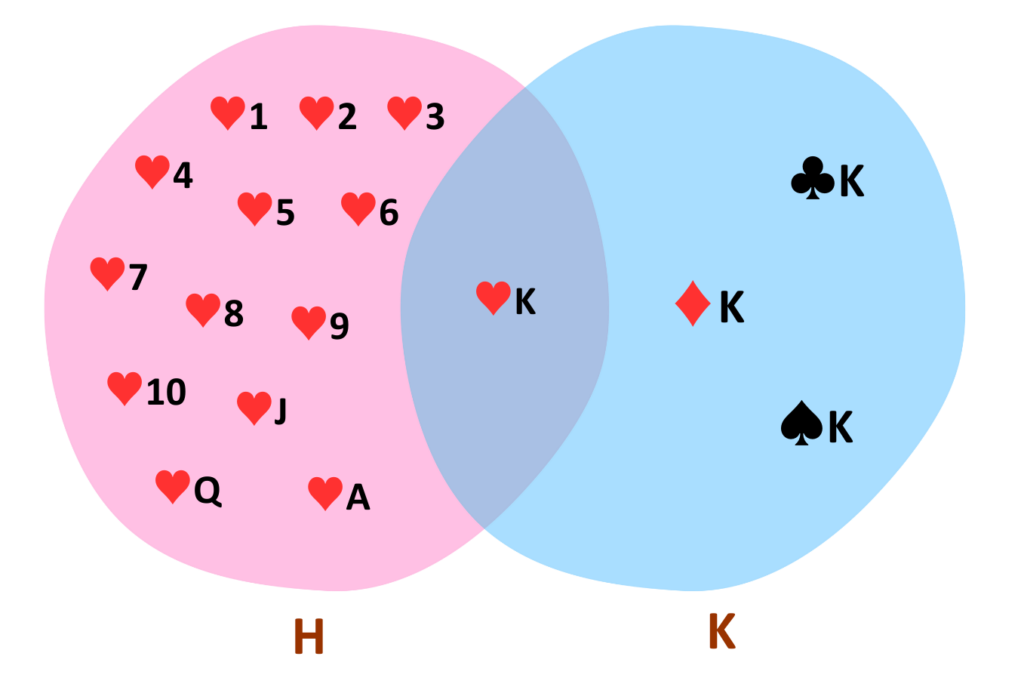
Venn Diagram example with playing cards showing set H for hearts and set K for kings with overlapping card king of hearts in intersection

Step #4: Calculate the Probabilities

Probability of an event,

Venn Diagram probability example using playing cards showing P of hearts P of kings and P not hearts with favorable outcomes and total outcomes

certified Physics and Maths tutorSolved Example:

Problem: Toss two fair coins A and B. Define two events:

  • Event A: At least one Head appears
  • Event B: Both coins show the same face

Find the Probability of P(A) and P(B).

Venn Diagram probability concept with two coin tosses showing hands flipping coins to represent sample space outcomes

Solution: 

Step #1: Define the Sample Space

All possible outcomes:

S = {HH,HT,TH,TT}

    • Total outcomes = 4

Step #2: Define the Events

    • Event A (At least one Head) = {HH, HT, TH}
    • Event B (Same face) = {HH, TT}
    • A ∩ B (Both A and B) = {HH}

Step #3: Draw the Venn Diagram

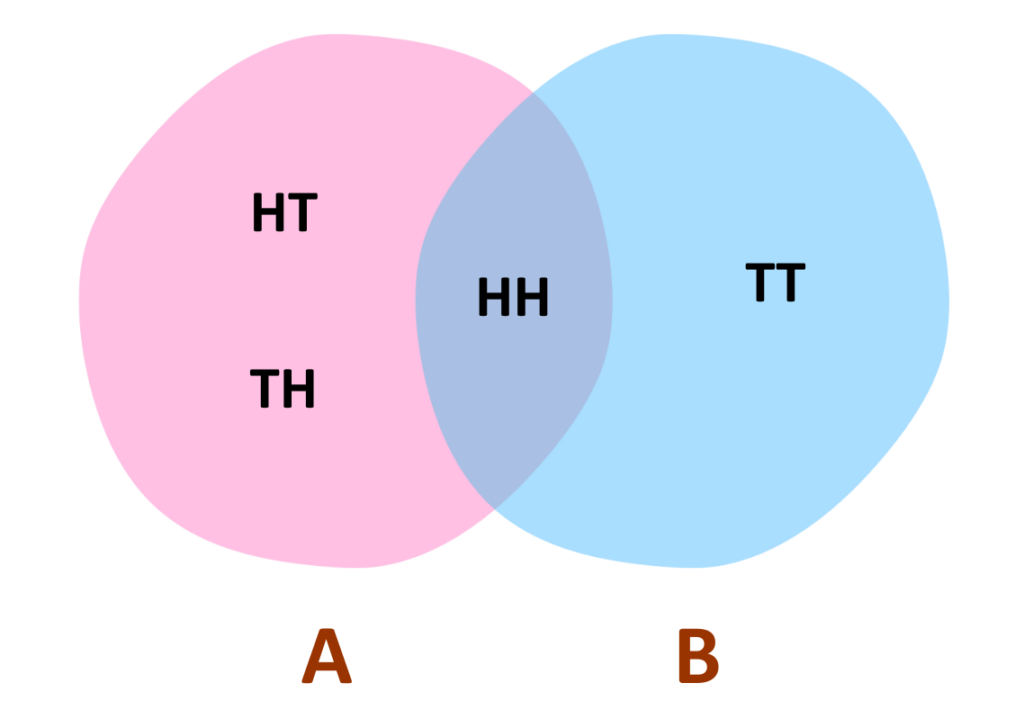
Venn Diagram showing sample space outcomes for two coin tosses with HT and TH in set A, TT in set B and HH in the intersection

Step #4: Calculate the Probabilities

Probability of an event,

Venn Diagram probability example showing calculation of P(A) and P(B) using favorable outcomes over total outcomes for two coin tosses

Table of Content