Sectors of Circles – GCSE Maths

Practice Questions
Downloads

Introduction

Circle is very important 2-Dimensional shape in geometry. Sector is a part of circle. Sector’s important characteristics are –

  • A Sector of circle is the portion made by two radii and the arc connecting the ends of those radii. The shape can be viewed as a pizza slice.

Diagram showing a circle divided into two labelled sectors with an arrow pointing from a quarter circle

  • The following are two sectors of same circle

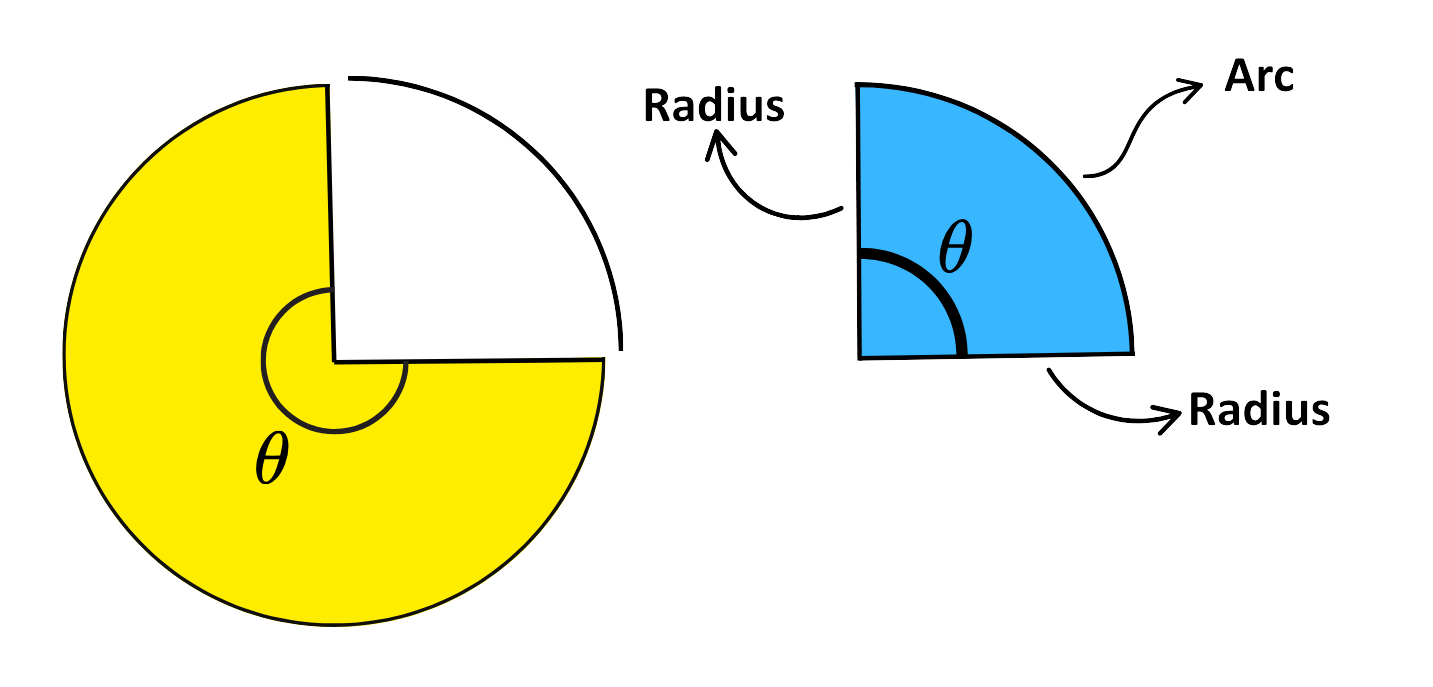
Two sectors of circles with angle theta, radius, and arc labelled in yellow and blue diagrams

Area of a Sector

  • A circle have a complete angle but Sector have a portion of it and we can represent the portion by writing it in fraction.

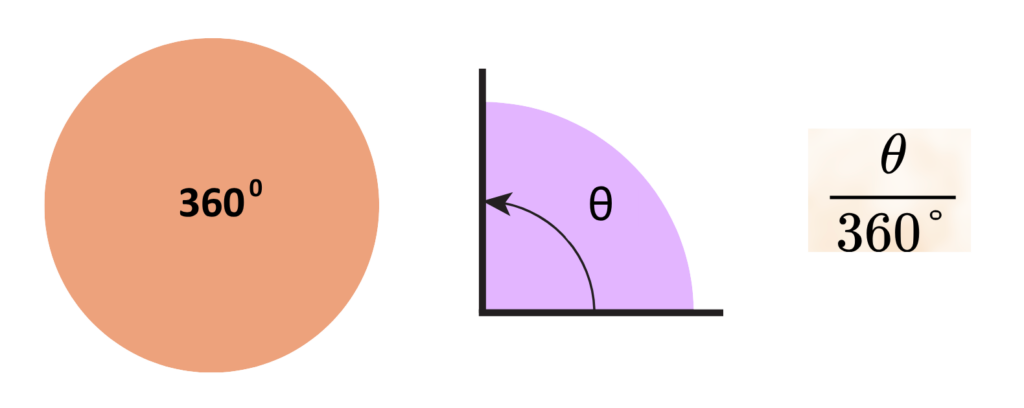
Circle with 360 degrees, a purple sector with angle theta, and the fraction theta over 360

  • The circle have an area equal to π(r)2, So Sector will have area equal to –

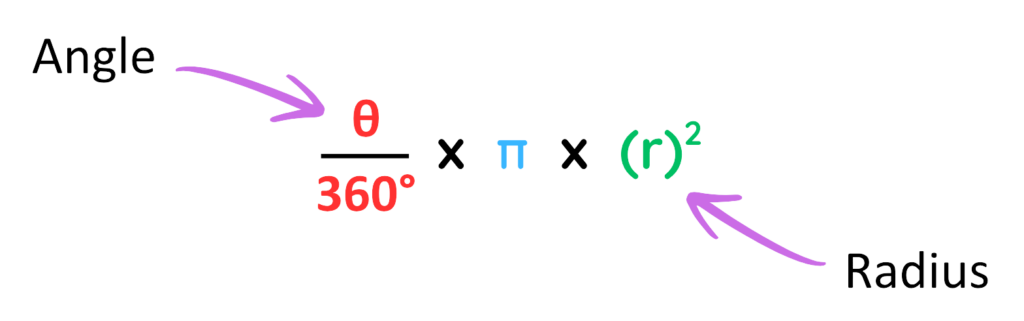
Formula for area of a sector: theta over 360 times pi times r squared, with angle and radius labeled

certified Physics and Maths tutorSolved Example

Problem: Find the area of following sectors

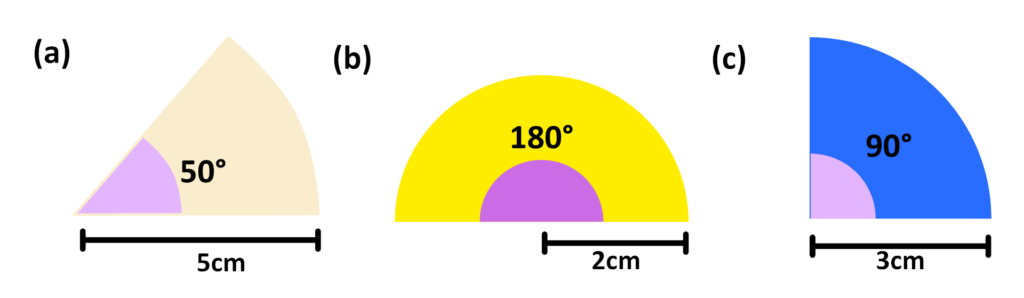
Three sector diagrams labeled (a), (b), and (c) showing angles of 50, 180, and 90 degrees with different radii

Solution: 

Formula for finding area of sector:

Formula to calculate area of a sector: theta over 360 times pi times r squared

(a) The area of sector with angle 50° and radius 5cm:

Worked example of area calculation for a sector with 50 degrees and radius 5 cm

(b) The area of sector with angle 180° and radius 2cm:

Worked example showing sector area calculation with 180 degrees and radius 2 cm

(c) The area of sector with angle 90° and radius 3cm:

Worked example showing area calculation of a sector with 90 degrees and radius 3 cm

Final Answer: (a) Area = 10.91 cm2 ,(b) Area = 6.28 cm2 , and (c) Area = 7.065 cm2

Arc length of a Sector

  • Sector is a part of circle similarly the arc of sector is part of the circumference of whole circle:

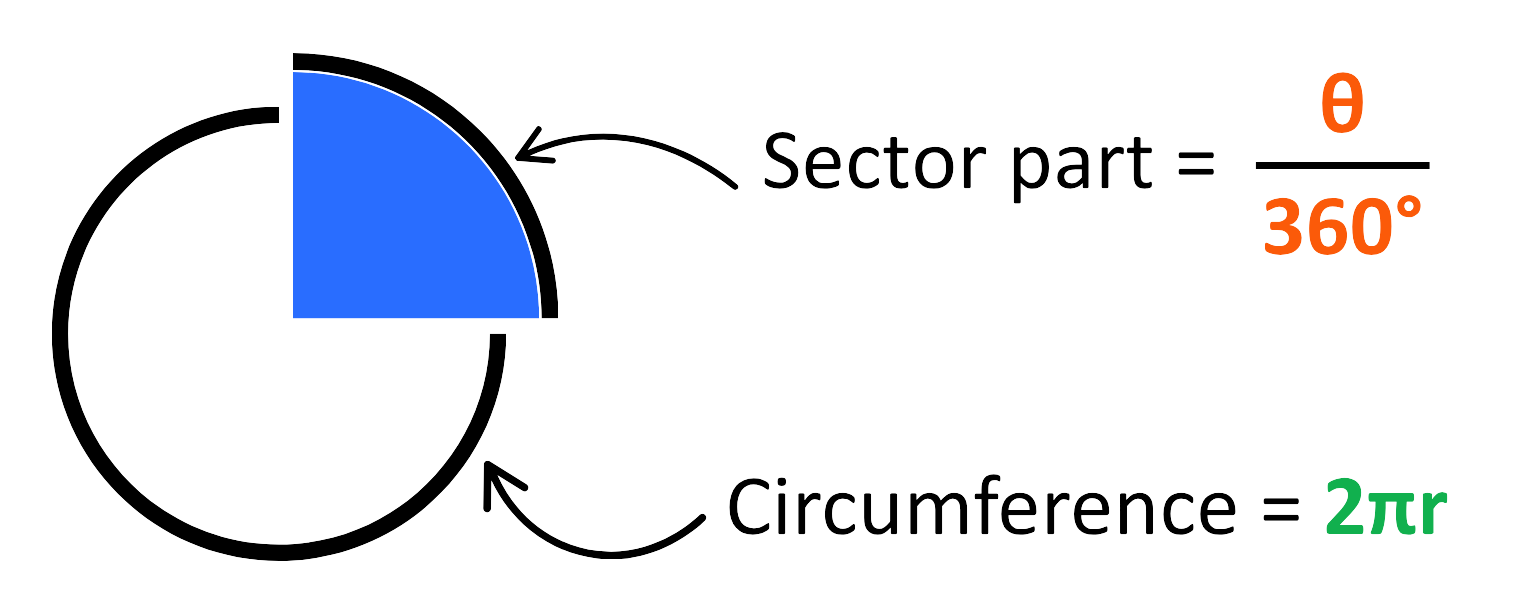
Circle with a blue sector showing sector part as theta over 360 and circumference as 2πr

  • Thus, the formula of Arc length of Sector part is –

Formula for arc length: theta over 360 times 2πr with labels for angle and diameter

certified Physics and Maths tutorSolved Example

Problem: Find out the arc length of the sector given in diagram

Sectors of Circles with 45 degree angle and 5 cm radius, with coloured arc and segment

Solution: 

The arc length of sector of circle with radius 5cm and angle 45°:

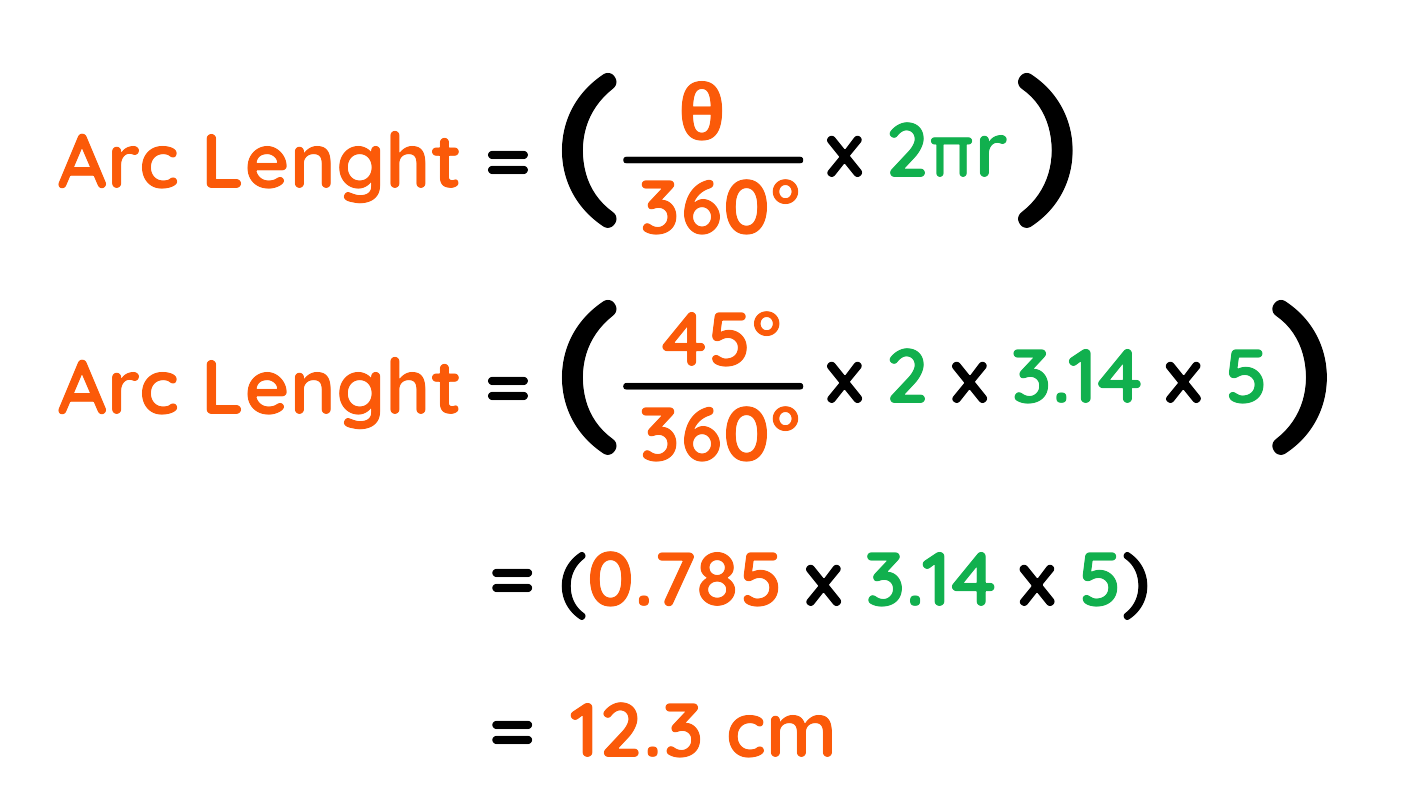
Sectors of Circles: Worked example showing arc length calculation with angle 45 degrees and radius 5 cm using arc length formula

Final Answer: Arc Length = 12.3 cm

certified Physics and Maths tutorSolved Example

Problem: Work out the arc length of the Sectors

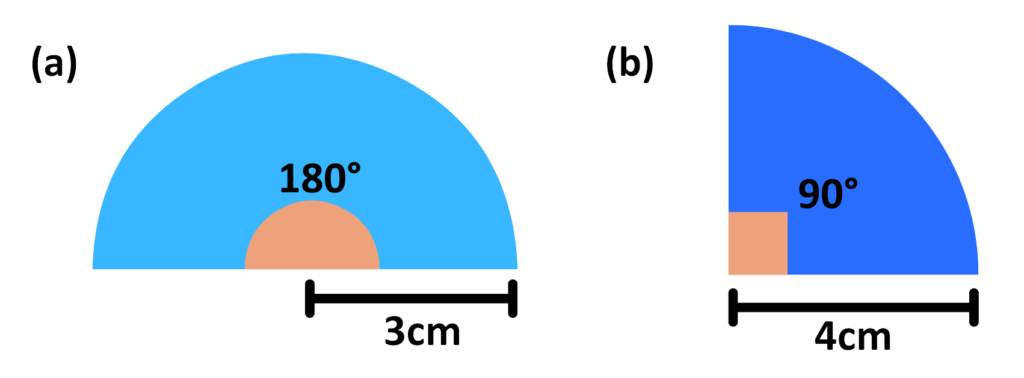
Sectors of Circles: Two diagrams of sectors labeled (a) and (b), showing 180 and 90 degree angles with inner shaded circles and radii 3 cm and 4 cm

Solution: 

The formula of finding arc length:

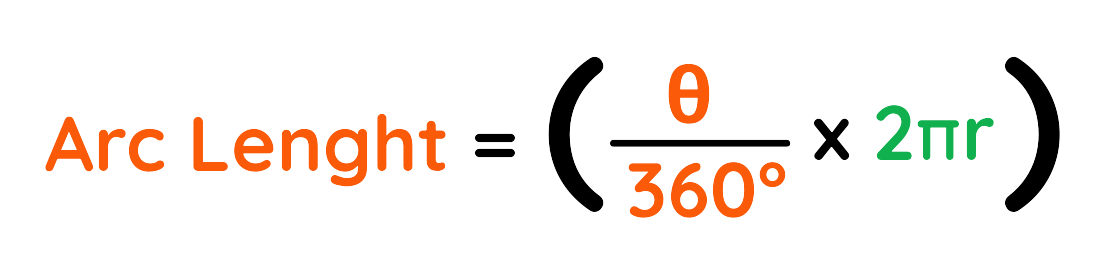
Sectors of Circles: Arc length formula showing theta over 360 times 2πr for sectors of circles

(a) Arc length of sector with radius 3cm and angle 180 degree:

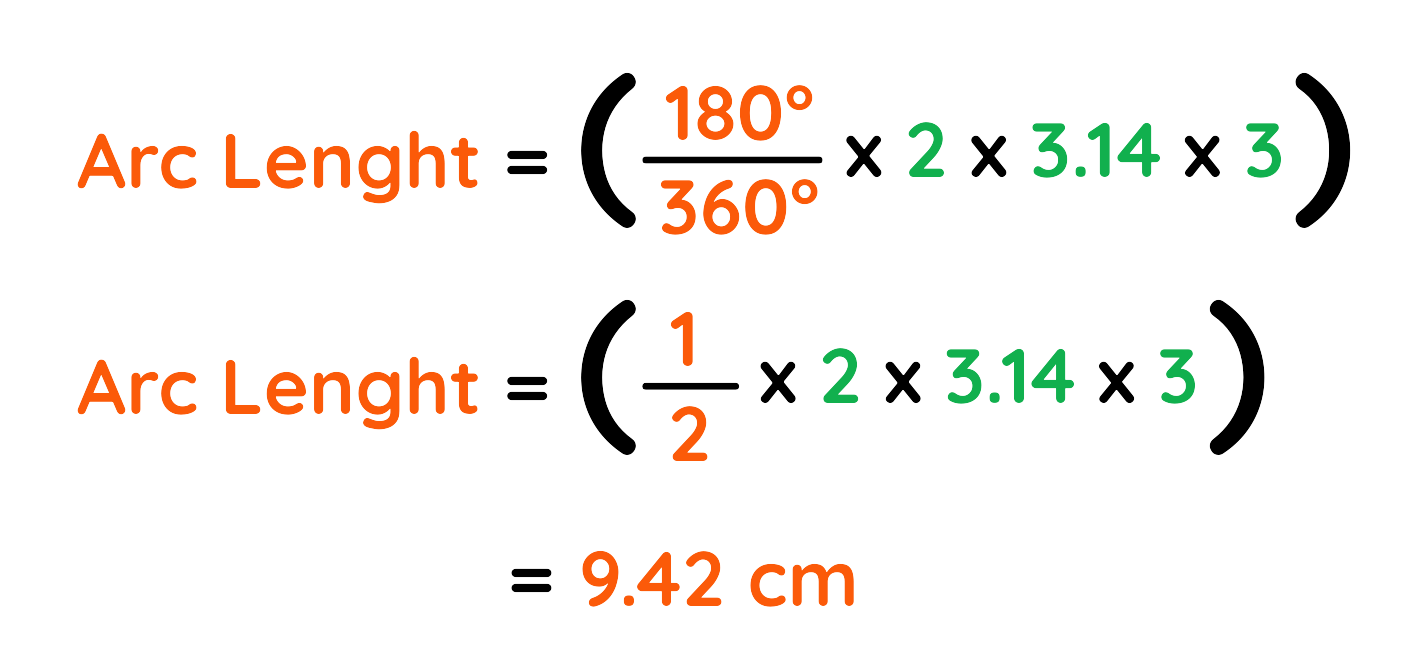
Sectors of Circles: Worked example calculating arc length for a 180 degree sector with radius 3 cm using formula

(b) Arc length of sector with radius 4cm and angle 90 degree:

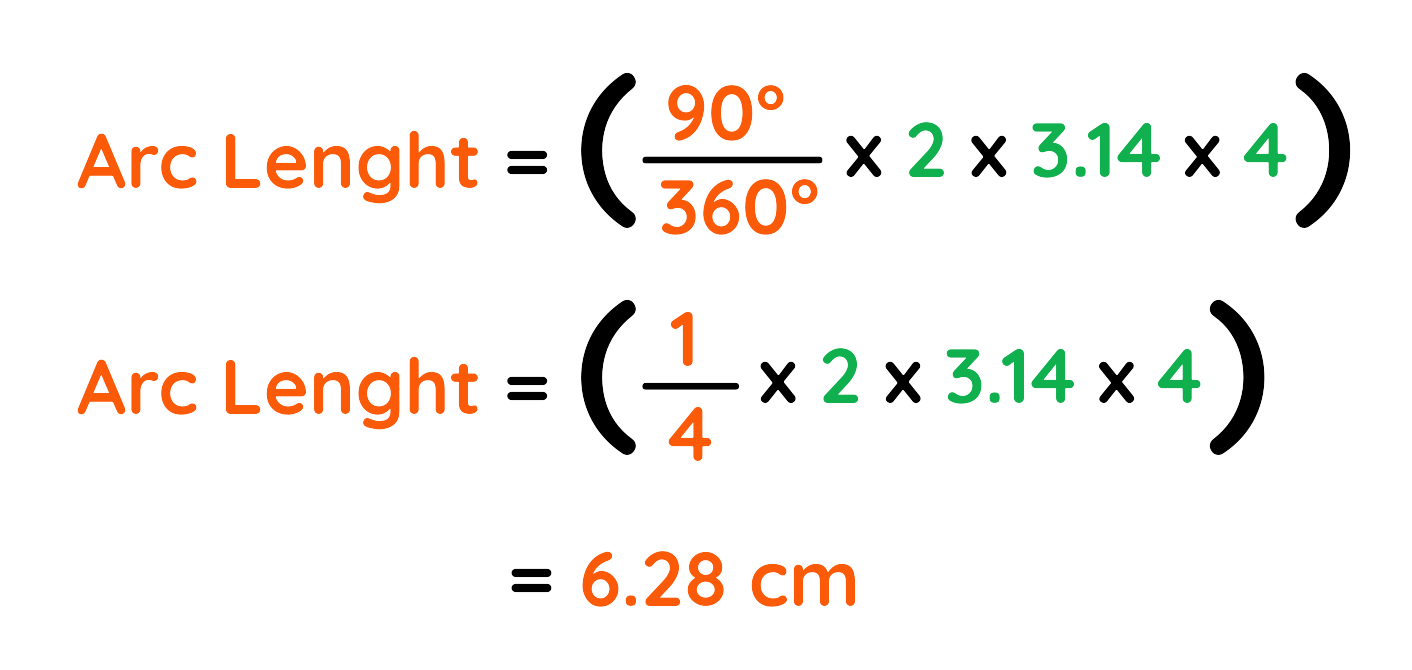
Sectors of Circles: Example showing how to calculate arc length of a 90 degree sector with radius 4 cm

Final Answer: (a) Arc Length = 9.42 cm and (b) Arc Length = 6.82 cm

certified Physics and Maths tutorSolved Example

Problem: Work out the Length of arc of sector and area of Sector the fan represents

Sector of a circle shown as an open hand fan with a 175 degree angle and 5 cm radius

Solution: 

The formula to find the area of sector and Arc Length:

Sectors of Circles: Formulas for area and arc length of a sector of a circle using angle theta and radius r

The area of the sector shown in diagram:

Sectors of Circles: Worked example showing how to calculate the area of a sector with 175 degrees and radius 5 cm

The arc length of sector shown in diagram:

Sectors of Circles: Step-by-step calculation of arc length for a sector with 175 degrees and radius 5 cm

Final Answer: area of the sector = 38.151 cm2 and arc length of sector = 15.2 cm

Request for Demo Lesson

Table of Content