Reverse Percentages – GCSE Maths
Reverse Percentage also known as “Reverse Percent“ is a mathematical operation that involves finding the original value or quantity from which a percentage was calculated.
What are Reverse Percentages?
- Reverse percentage is a mathematical concept which is used to find or determine the original value before the Percentage Increase or Decrease.
- Start with the final amount after a percentage change and work backward to find the original number.
- If you know the final value after a percentage change, reverse percentages help you find the original value before the change.
Formula used in Reverse Percentages:

 Solved Example
Solved Example
Problem: A TV now costs £300 after a 25% increase. What was its original price?
Solution:
Step #1: Given:
- New value = £300
- Percentage increased = 25%
Step #2: Applying the formula:

Step #3: Put the values in formula:

Step #4: Simplify the denominator:
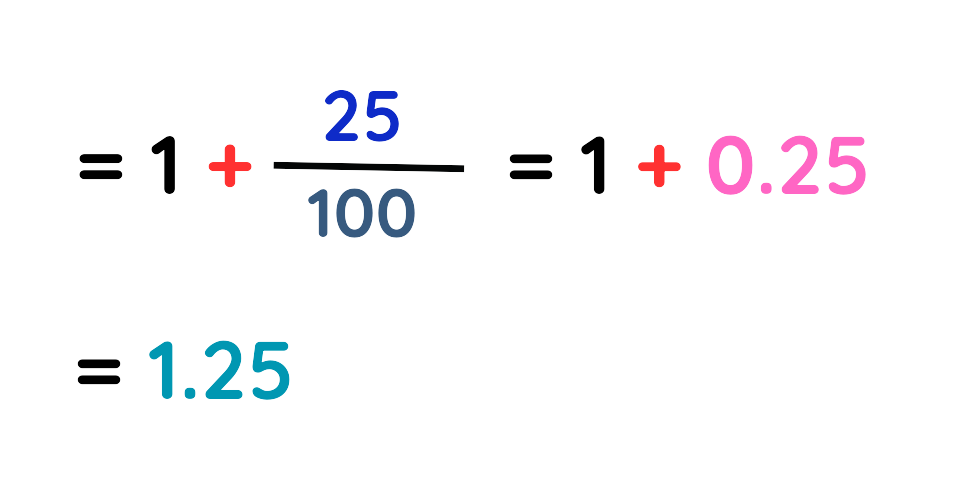
Step #5: The final value is:
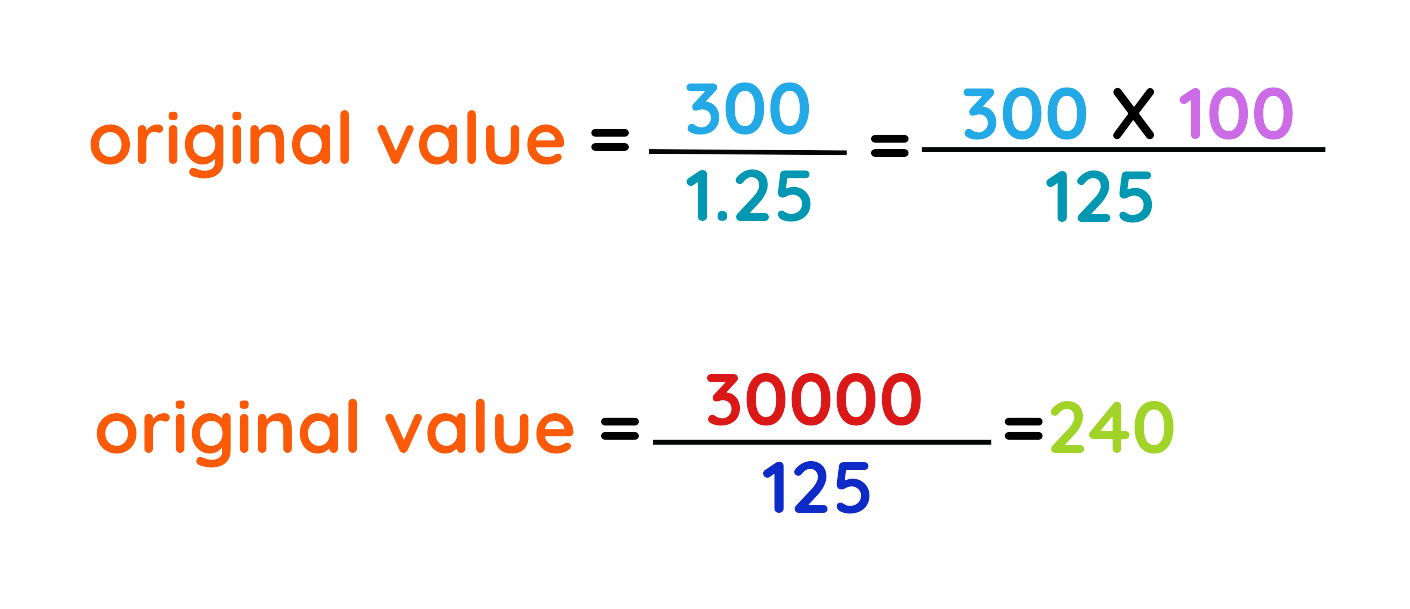
The original price of TV was £240.
Final Answer: £240
How Reverse Percentage is Different From Original Percentage?

Original Percentages:
- It is use when we know the original number or value and want to calculate a percentage of it.
- If original price of shirt is £100 then after 20% increase, the new price will be £120.
Reverse Percentages:
- It is use when we know the final value after a percentage change and want to find the original value.
- After a 20 % increase, the new price of a shirt is £120 then the original price of a shirt was £100.
Steps to Solve Reverse Percentages
Step#1: Understand the Question
- Check the new value is increased or decreased after the change of original value:
- If the final value is after a percentage increase, the formula is:

- If the final value is after a percentage decrease, the formula is:

Step#2: Work out what percentage you now have.
Step#3: Solve the equation
- We know the original equivalent percentage for all the process is 100%.
- Use this to find the 1% of original price or value.
Step#4: Now multiply the 1% with 100% to get the original value or price.
Note: To solve this easily, we should also know the concept of Original Percentages.
Three Additional Solved Examples
 Solved Example 1
Solved Example 1
Problem: A jacket costs £60 after a 20% discount. What was the original price?
Solution:
Step #1: Given:
- New value = £60
- Percentage increased = 20%
Step #2: Applying the formula:

Step #3: Put the values in formula:

Step #4: Simplify the denominator:
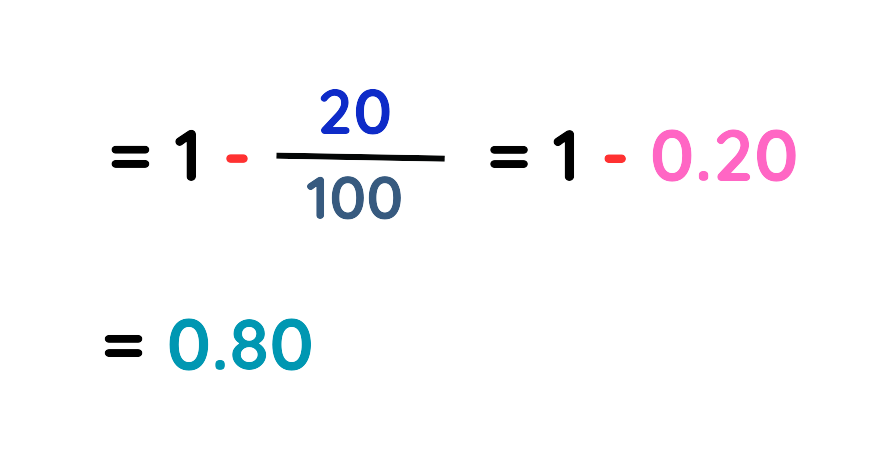
Step #5: The final value is:
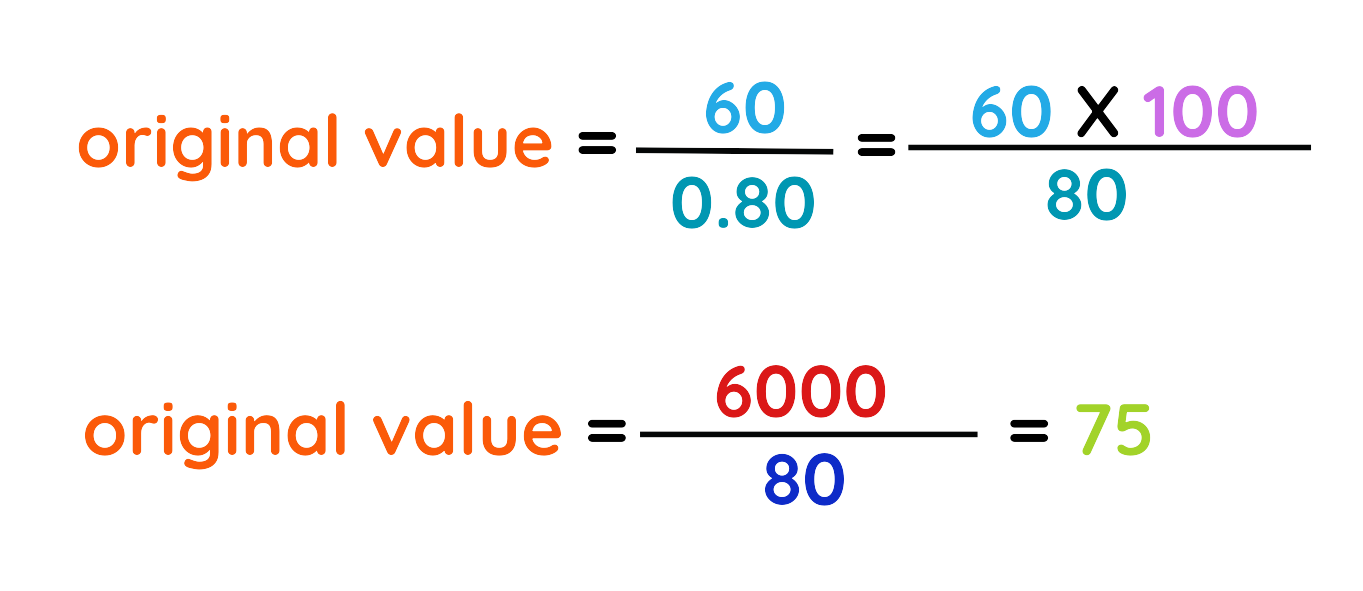
The original price of jacket was £75.
Final Answer: £75
 Solved Example 2
Solved Example 2
Problem: A product costs £120 including 20% VAT. What was the price before tax?
Solution:
Step #1: Given:
- New value = £120
- Percentage increased = 20%
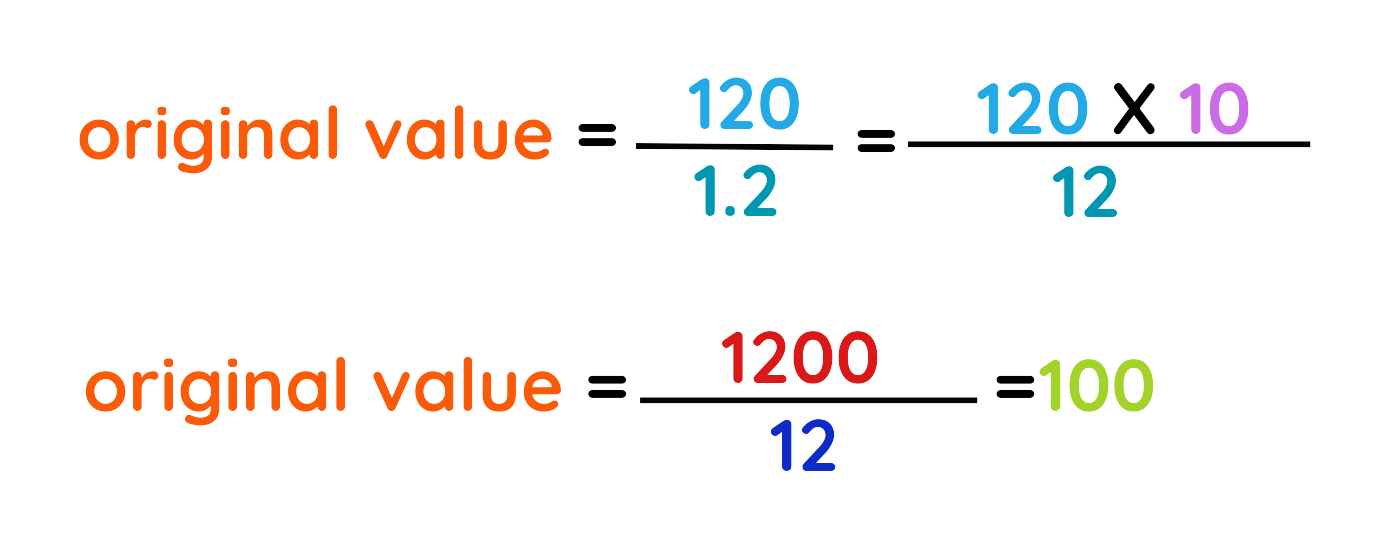
Step #2: Applying the formula:

Step #3: Put the values in formula:

Step #4: Simplify the denominator:
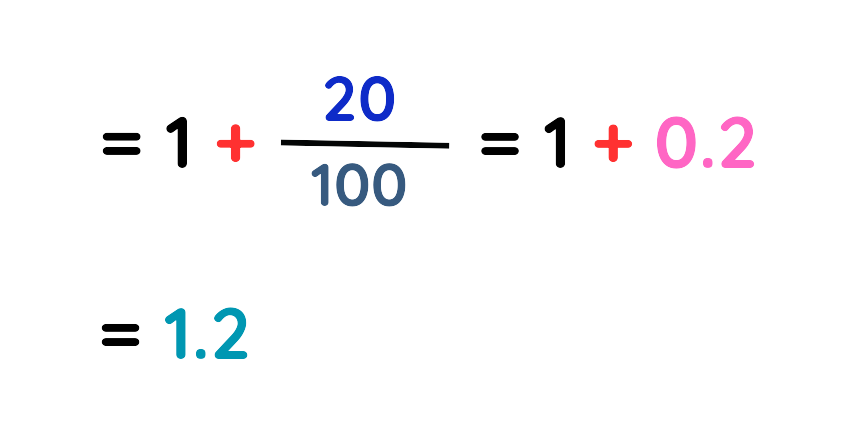
Step #5: The final value is:
The original price of product was £100.
Final Answer: £100
 Solved Example 3
Solved Example 3
Problem: A house increased in value by 15% and is now worth £230,000. What was its original price?
Solution:
Step #1: Given:
- New value = £230,000
- Percentage increased = 15%
Step #2: Applying the formula:

Step #3: Put the values in formula:
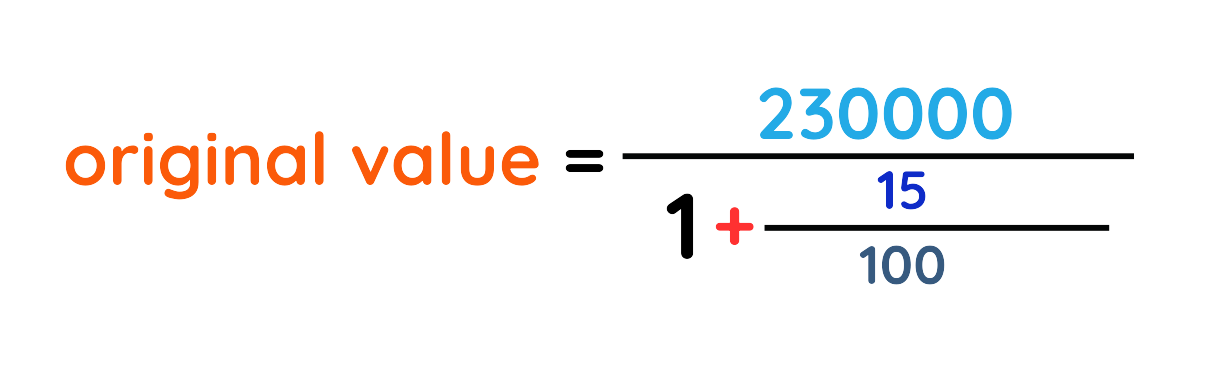
Step #4: Simplify the denominator:
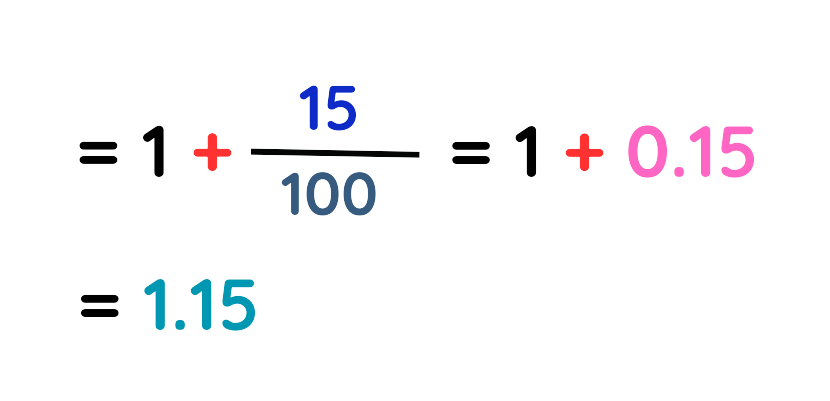
Step #5: The final value is:

The original price of house was £200,000.
Final Answer: £200,000
Practice Questions and Answers on Reverse Percentages
Question 1: A shirt is on sale for £60 after a 20% discount. What was the original price?
Question 2: After a 15% increase, the price of a phone is £345. What was the original price?
Question 3: A house is now valued at £110,000 after a 10% decrease. What was the original price?
Question 4: The price of a book is £25 after a 30% increase. What was the original price?
Question 5: A laptop is now £850 after a 25% discount. What was the original price?
Question 6: A company’s revenue is £1,27,500after a 12.5% decrease due to economic downturn. What was the original revenue before the decrease?
Question 7: A car’s price increased by 18% and is now valued at £4,720. What was the original price before the increase?
Question 8: A company reduced its workforce by 22%, leaving 4,290 employees. How many employees did the company originally have?
Question 9: The price of gold increased by 27%, and the new price is £1,397 per ounce. What was the original price?
Question 10: A business made £315,800 in profit after a 19.5% loss compared to the previous year. What was the previous year’s profit?
Solutions
Question 1:
Solution:
Step#1: Given
• New value = £60
• Percentage decreased = 20%
Step#2: Applying the formula
Original Value = Final Value ÷ (1 ± Percentage ÷ 100)
Step#3: Put the values in the formula
Original Value = 60 ÷ (1 − 20 ÷ 100)
Step#4: Simplify the denominator
= 1 − 20 ÷ 100 = 1 − 0.2
= 0.8
Step#5: The final value is
Original Value = 60 ÷ 0.8
= 60 × 10 ÷ 8
= 600 ÷ 8 = 75
The original price of the shirt was £75
Question 2:
Solution:
Step#1: Given
• New value = £345
• Percentage increased = 15%
Step#2: Applying the formula
Original Value = Final Value ÷ (1 ± Percentage ÷ 100)
Step#3: Put the values in the formula
Original Value = 345 ÷ (1 + 15 ÷ 100)
Step#4: Simplify the denominator
= 1 + 15 ÷ 100 = 1 + 0.15
= 1.15
Step#5: The final value is
Original Value = 345 ÷ 1.15
= 345 × 100 ÷ 115
= 34500 ÷ 115 = 300
The original price of the phone was £300
Question 3:
Solution:
Step#1: Given
• New value = £110,000
• Percentage decreased = 10%
Step#2: Applying the formula
Original Value = Final Value ÷ (1 ± Percentage ÷ 100)
Step#3: Put the values in the formula
Original Value = 110000 ÷ (1 − 10 ÷ 100)
Step#4: Simplify the denominator
= 1 − 10 ÷ 100 = 1 − 0.1
= 0.9
Step#5: The final value is
Original Value = 110000 ÷ 0.9
= 110000 × 10 ÷ 9
= 1100000 ÷ 9 = 122222.22
The original price of the house was £122,222.22
Question 4:
Solution:
Step#1: Given
• New value = £25
• Percentage increased = 30%
Step#2: Applying the formula
Original Value = Final Value ÷ (1 ± Percentage ÷ 100)
Step#3: Put the values in the formula
Original Value = 25 ÷ (1 + 30 ÷ 100)
Step#4: Simplify the denominator
= 1 + 30 ÷ 100 = 1 + 0.3
= 1.3
Step#5: The final value is
Original Value = 25 ÷ 1.3
= 25 × 10 ÷ 13
= 250 ÷ 13 = 19.23
The original price of the book was £19.23
Question 5:
Solution:
Step#1: Given
• New value = £850
• Percentage decreased = 25%
Step#2: Applying the formula
Original Value = Final Value ÷ (1 ± Percentage ÷ 100)
Step#3: Put the values in the formula
Original Value = 850 ÷ (1 − 25 ÷ 100)
Step#4: Simplify the denominator
= 1 − 25 ÷ 100 = 1 − 0.25
= 0.75
Step#5: The final value is
Original Value = 850 ÷ 0.75
= 850 × 100 ÷ 75
= 85000 ÷ 75 = 1133.33
The original price of the laptop was £1133.33
Question 6:
Solution:
Step#1: Given
• New value = £127,500
• Percentage decreased = 12.5%
Step#2: Applying the formula
Original Value = Final Value ÷ (1 ± Percentage ÷ 100)
Step#3: Put the values in the formula
Original Value = 127500 ÷ (1 − 12.5 ÷ 100)
Step#4: Simplify the denominator
= 1 − 12.5 ÷ 100 = 1 − 0.125
= 0.875
Step#5: The final value is
Original Value = 127500 ÷ 0.875
= 127500 × 1000 ÷ 875
= 127500000 ÷ 875 = 145714.28
The original revenue of the company was £145,714.28
Question 7:
Solution:
Step#1: Given
• New value = £4720
• Percentage increased = 18%
Step#2: Applying the formula
Original Value = Final Value ÷ (1 ± Percentage ÷ 100)
Step#3: Put the values in the formula
Original Value = 4720 ÷ (1 + 18 ÷ 100)
Step#4: Simplify the denominator
= 1 + 18 ÷ 100 = 1 + 0.18
= 1.18
Step#5: The final value is
Original Value = 4720 ÷ 1.18
= 4720 × 100 ÷ 118
= 472000 ÷ 118 = 4000
The original price of the car was £4000
Question 8:
Solution:
Step#1: Given
• New value = 4290
• Percentage decreased = 22%
Step#2: Applying the formula
Original Value = Final Value ÷ (1 ± Percentage ÷ 100)
Step#3: Put the values in the formula
Original Value = 4290 ÷ (1 − 22 ÷ 100)
Step#4: Simplify the denominator
= 1 − 22 ÷ 100 = 1 − 0.22
= 0.78
Step#5: The final value is
Original Value = 4290 ÷ 0.78
= 4290 × 100 ÷ 78
= 429000 ÷ 78 = 5500
The original number of employees in the company was 5500
Question 9:
Solution:
Step#1: Given
• New value = £1397
• Percentage increased = 27%
Step#2: Applying the formula
Original Value = Final Value ÷ (1 ± Percentage ÷ 100)
Step#3: Put the values in the formula
Original Value = 1397 ÷ (1 + 27 ÷ 100)
Step#4: Simplify the denominator
= 1 + 27 ÷ 100 = 1 + 0.27
= 1.27
Step#5: The final value is
Original Value = 1397 ÷ 1.27
= 1397 × 100 ÷ 127
= 139700 ÷ 127 = 1100
The original price of gold was £1100
Question 10:
Solution:
Step#1: Given
• New value = £315,800
• Percentage decreased = 19.5%
Step#2: Applying the formula
Original Value = Final Value ÷ (1 ± Percentage ÷ 100)
Step#3: Put the values in the formula
Original Value = 315800 ÷ (1 − 19.5 ÷ 100)
Step#4: Simplify the denominator
= 1 − 19.5 ÷ 100 = 1 − 0.195
= 0.805
Step#5: The final value is
Original Value = 315800 ÷ 0.805
= 315800 × 1000 ÷ 805
= 315800000 ÷ 805 = 392298.13
The original revenue of the company was £392,298.13

