Law of Sine and Cosine Rule – GCSE Maths

Practice Questions
Downloads

Introduction

  • Laws of Sine and Cosine are trigonometric formulas used to solve triangles when certain information is given.
  • They are especially useful for non-right triangles.
  • These laws are fundamental in trigonometry and have applications in physics, engineering, and navigation.

What is the Sine Rule?

  • The Sine Rule is a fundamental trigonometric formula that relates the sides of a triangle to the sines of their opposite angles.
  • Mathematically,

For any triangle with sides a, b and c opposite angles A, B and C respectively, for finding missing side:

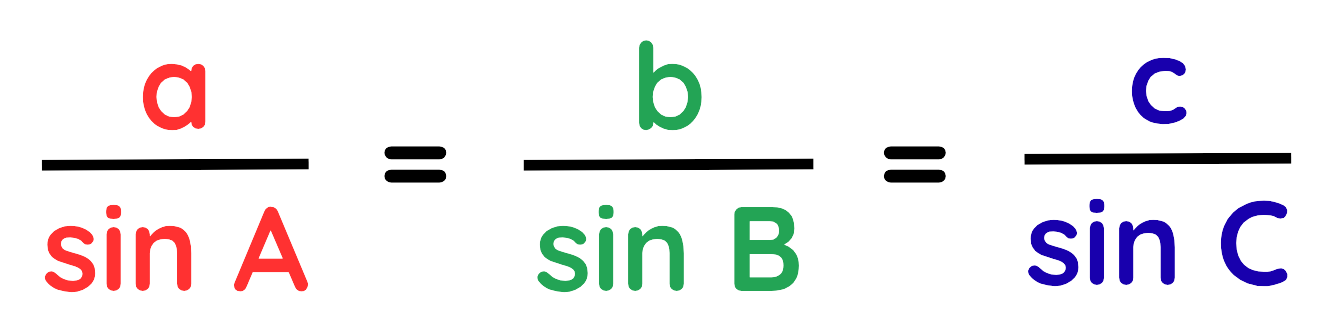
Alternatively, it can be written as for finding missing angle:

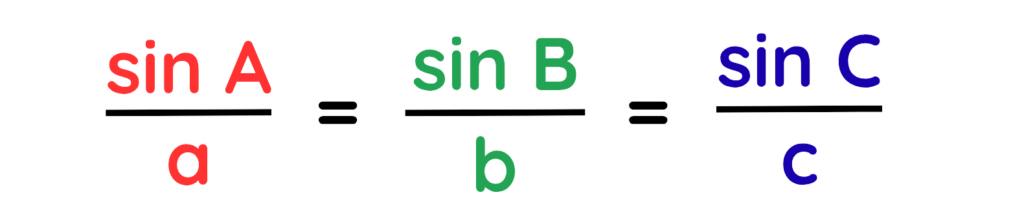
Law of Sine rule formula showing sin A over a equals sin B over b equals sin C over c for triangle calculation

Where:

    • a, b and c are the lengths of the sides of the triangle
    • A, B and C are the angles opposite those sides

certified Physics and Maths tutorSolved Example

Problem: A = 40∘, B = 60∘ and side a = 10 cm. Find side b.

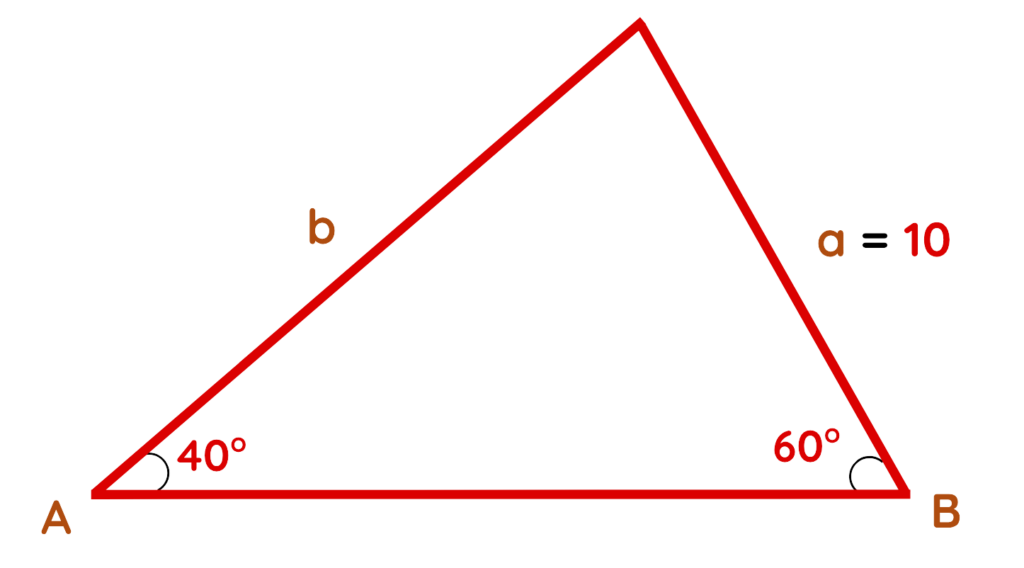
Triangle with sides and angles labeled for Law of Sine calculation showing side a equals 10 and angles 40 and 60 degrees

Solution: 

Use the formula

Law of Sine rearrangement to calculate unknown side b using angles and side a

Put the values:

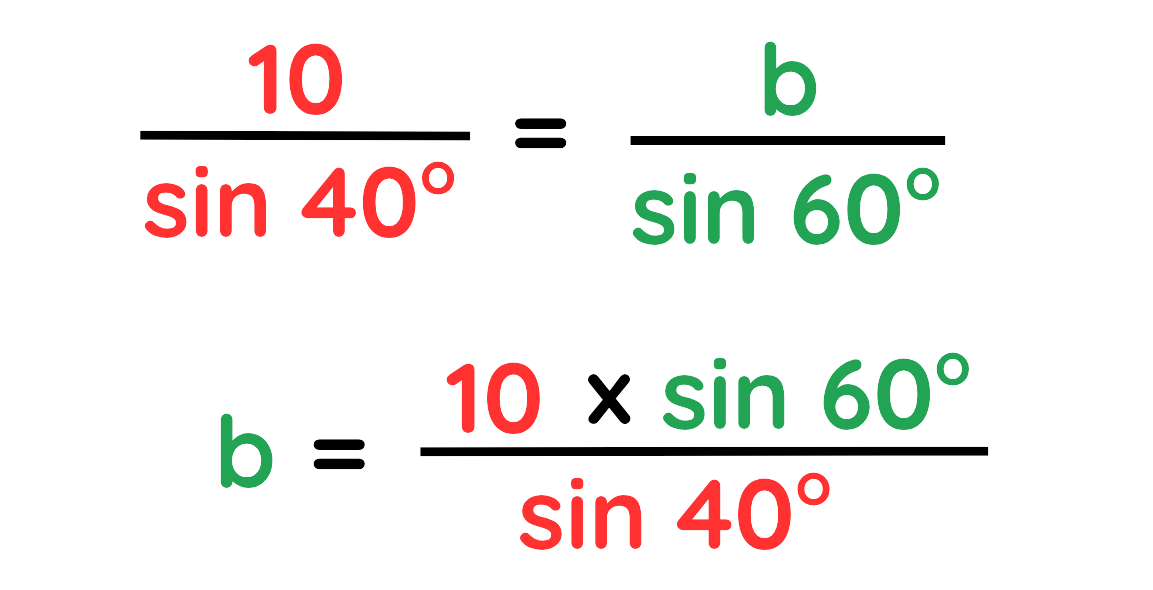
Law of Sine example showing how to rearrange the formula to calculate an unknown side

Now calculate using a calculator:

Law of Sine calculation showing final value of side b using sine values

Final Answer: b = 13.5 cm

What is the Cosine Rule?

  • The Cosine Rule is also a trigonometric formula used to find a side or angle in a triangle.
  • It works for any triangle whether it’s acute, obtuse, or right-angled.
  • Mathematically,

For any triangle with sides a, b and c opposite angles A, B and C opposite those sides:

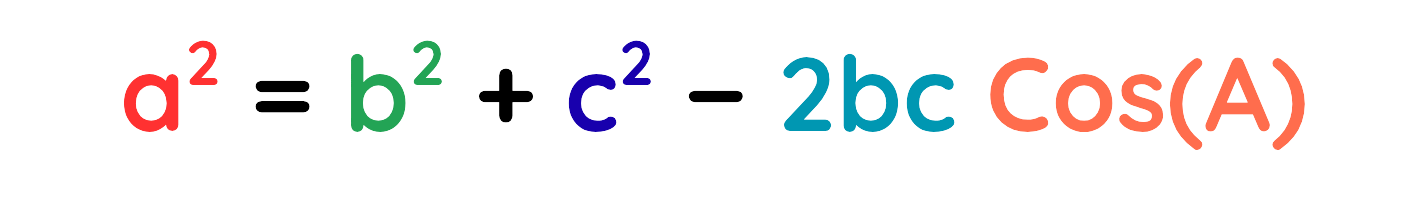
Cosine Rule formula a² = b² + c² - 2bc cos A

If you know all three sides, then we can find an angle using this rearranged version of the cosine rule:

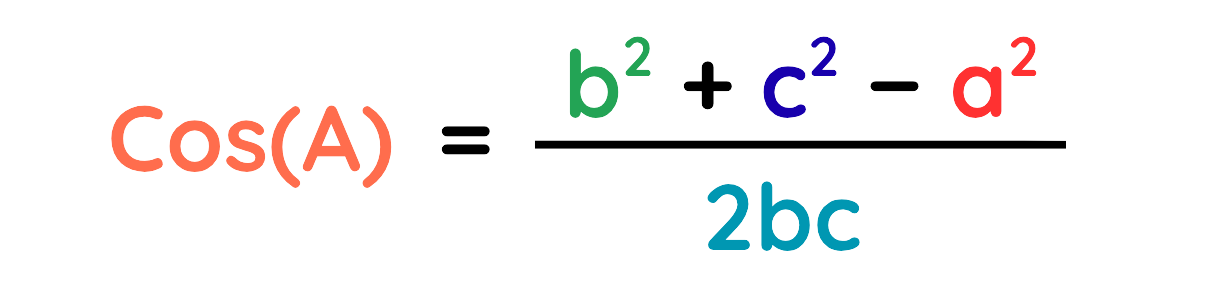
Cosine Rule rearranged formula to calculate angle A

Where:

    • a, b and c are the lengths of the sides of the triangle.
    • A, B and C are the angles opposite those sides.

certified Physics and Maths tutorSolved Example

Problem: Side a = 5cm, side b = 7 cm, angle C = 60∘. Find side c.

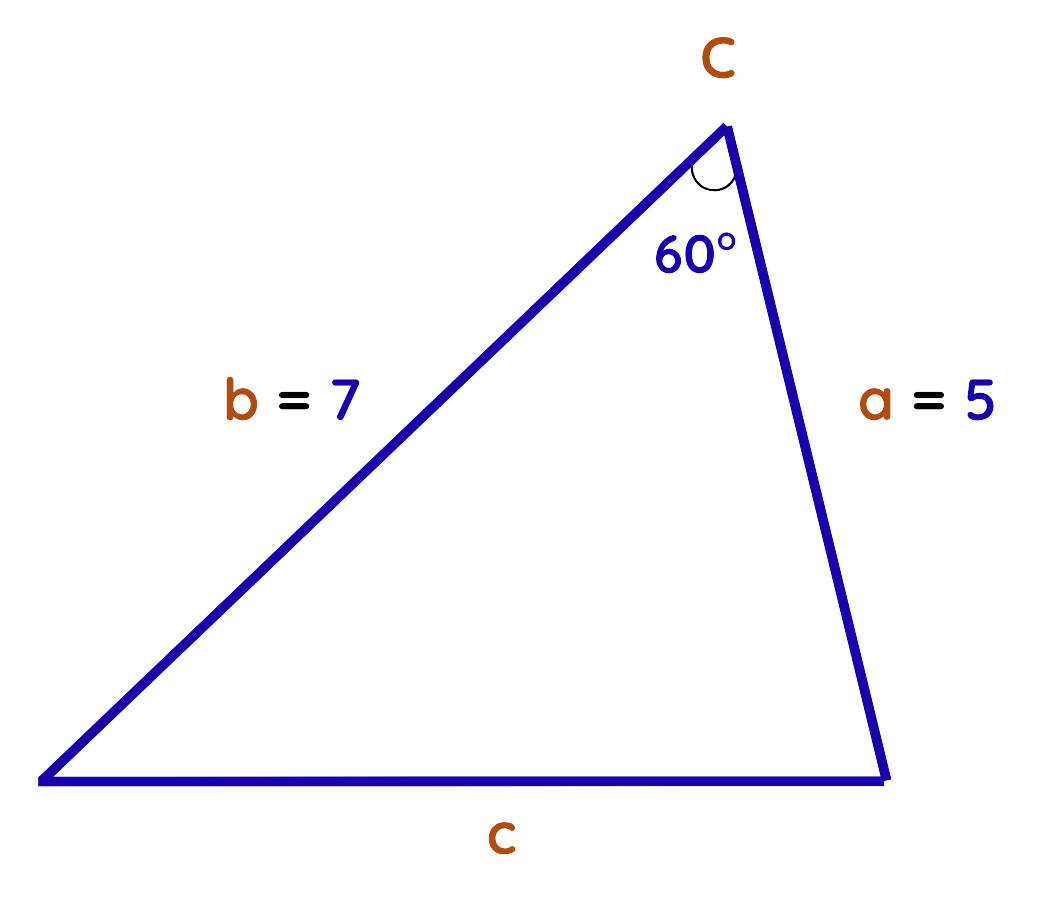
Triangle with two sides and included angle for Cosine Rule

Solution: 

Use the formula:

Cosine Rule formula for triangle side calculation

Put the values:

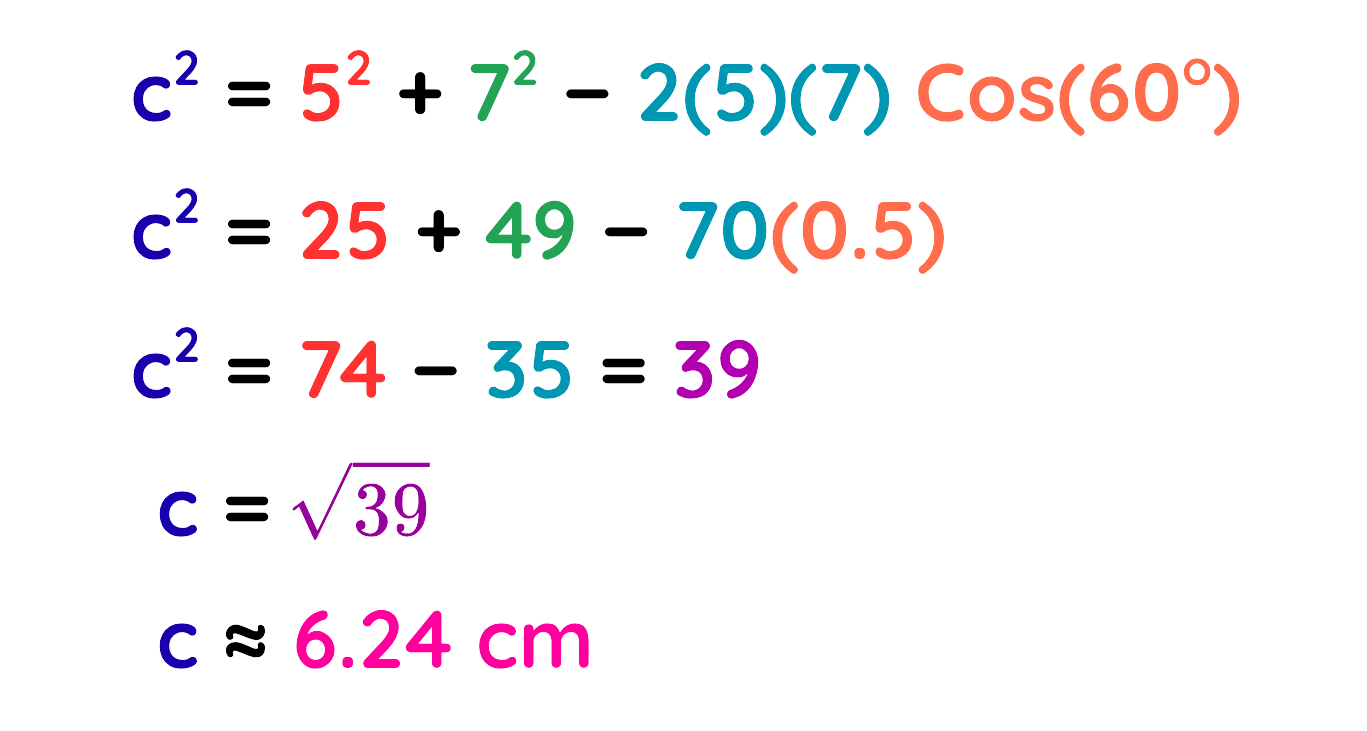
Cosine Rule calculation example with working steps

Final Answer: c = 6.24 cm

How to Find Missing Side and Angle?

  • The Sine Rule or the Cosine Rule, both are used to find the missing side or missing angle depending on what information is given in the question.

Use the Sine Rule:

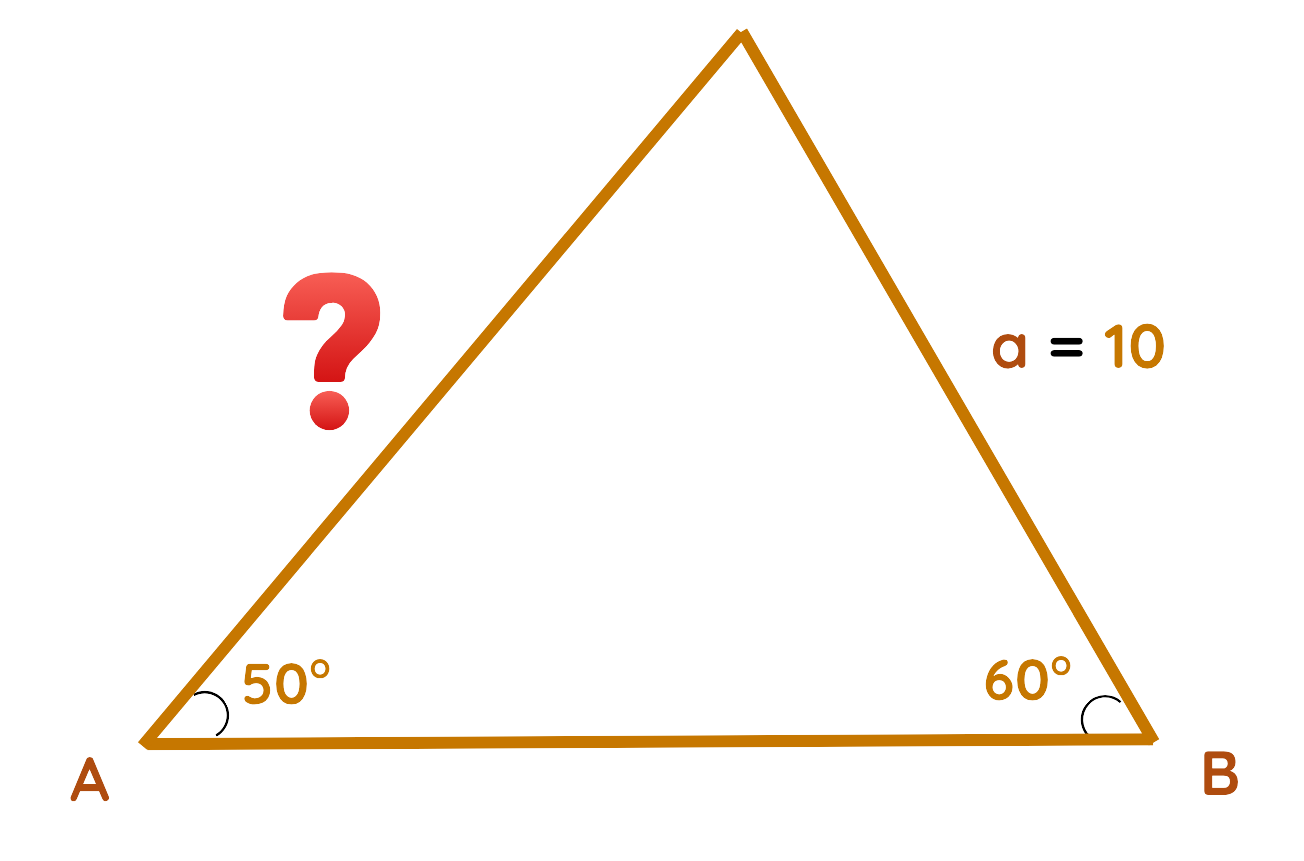
  • If we know the 2 angles and one side, then we use it to find another side

Triangle with two angles and one side given to find missing side using Law of Sines

  • If we know the 2 sides and one non-included angle, then we use it to find the other angle.

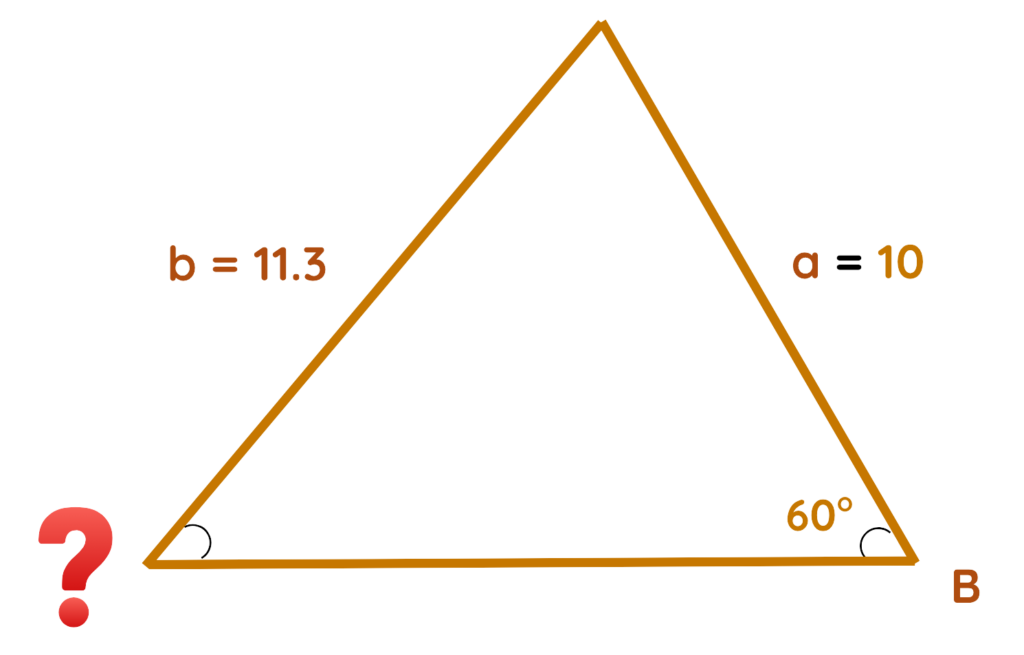
Triangle with two sides and one angle given to find missing angle using Law of Sines

Use the Cosine Rule:

  • If we know the 2 sides and one included angle, then we use it to find third side.

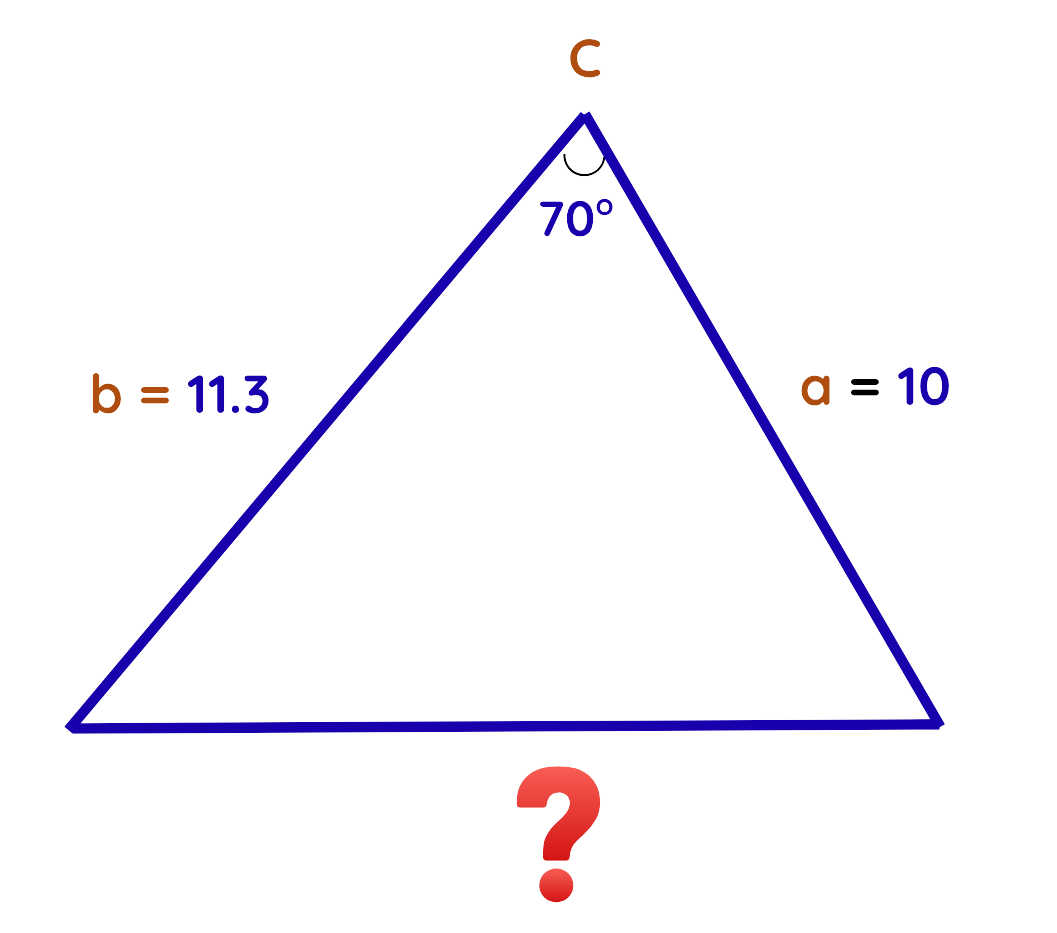
Triangle with two sides and included angle given to find the missing side using Law of Cosines

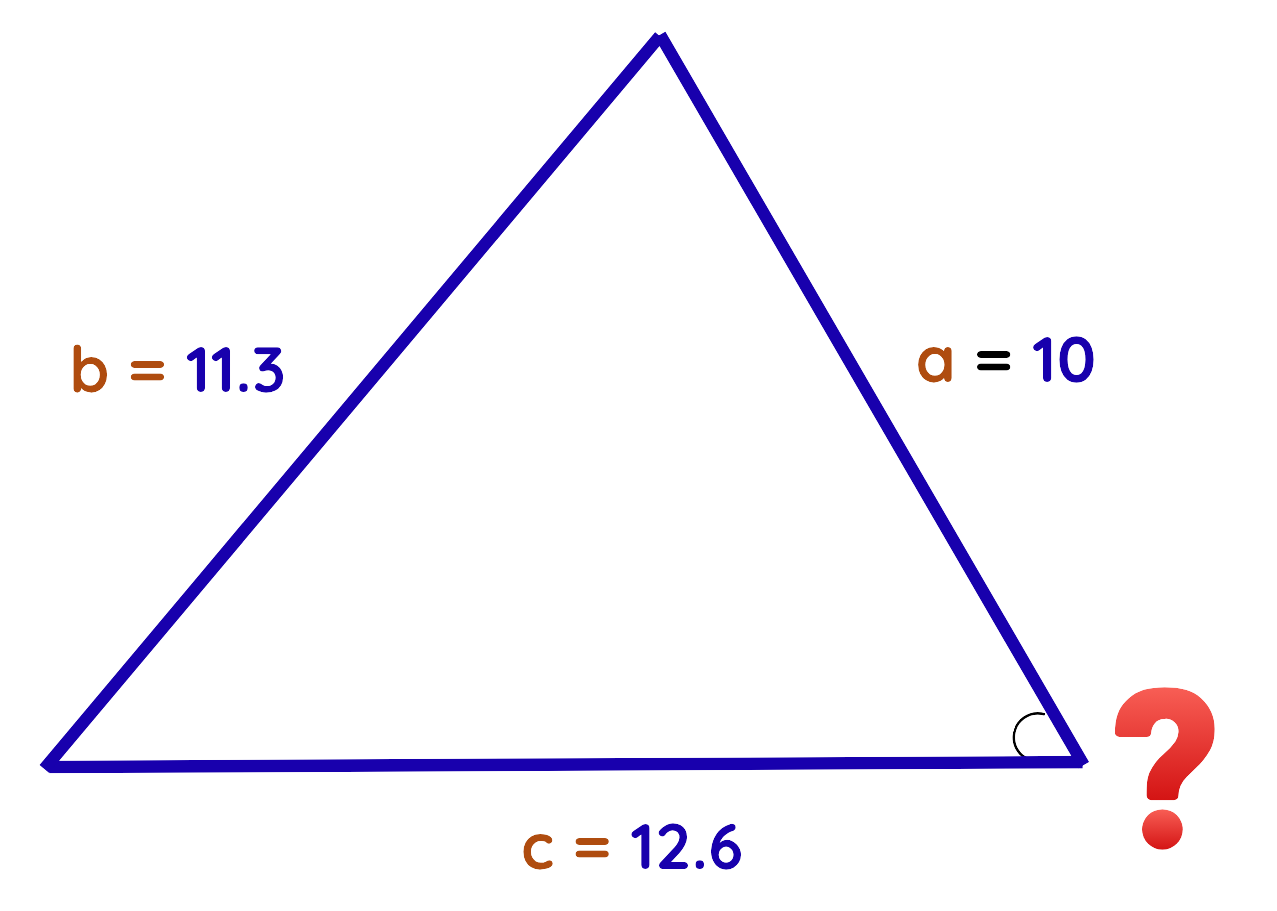
  • If we know all the three sides, then we use it to find any angle.

Triangle with all three sides given to find the missing angle using Law of Cosines

Steps to Find the Missing Side or Angle:

  • Step#1: Identify the known values.
  • Step#2: Write the formula based on the side or angle you’re finding.
  • Step#3: Plug the values.
  • Step#4: Solve for the missing value.

certified Physics and Maths tutorSolved Example

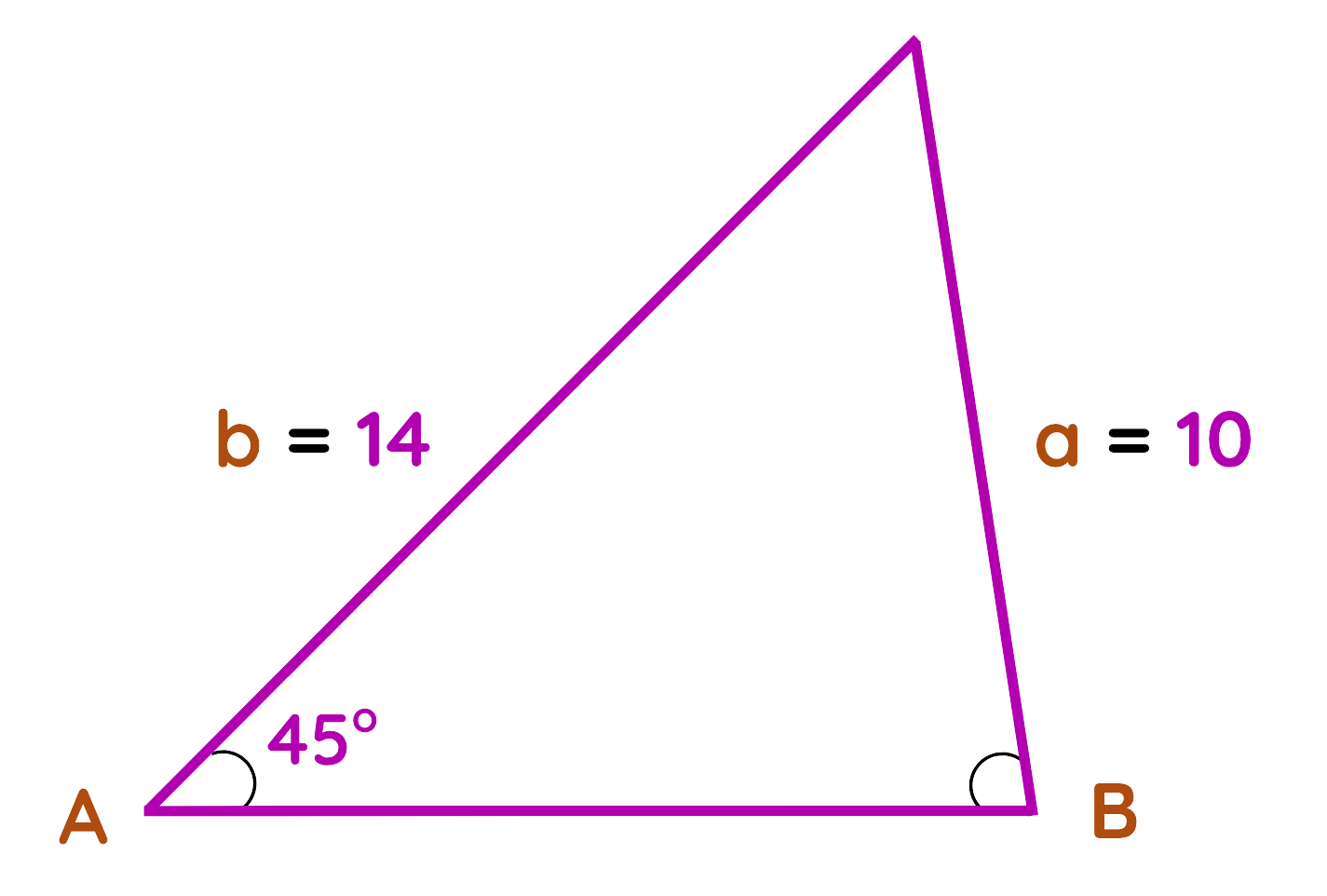
Problem: In Triangle ABC, Side a = 10cm, Side b = 14cm and Angle A = 45°. Find angle B.

Triangle with sides 10 cm and 14 cm and angle 45 degrees for Law of Sine or Cosine calculation

Solution: 

Step#1: Given:

    • Side a = 10 cm
    • Side b = 14 cm
    • Angle A = 45°

Step#2: Use The Formula:

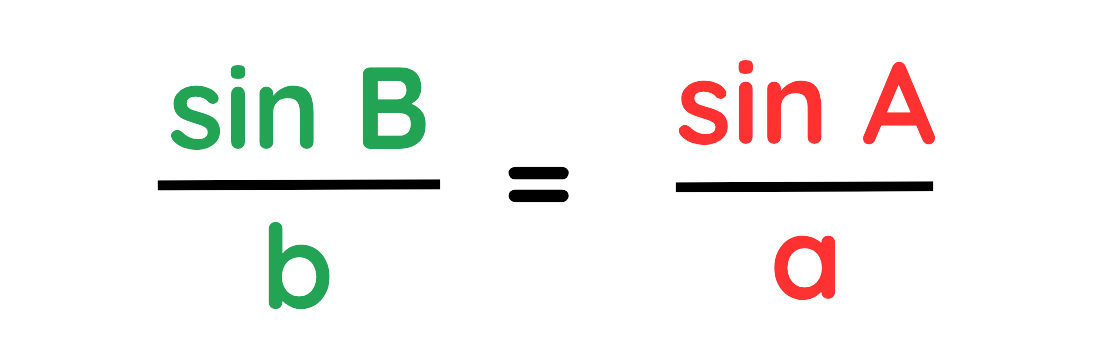
Rearranged Sine Rule formula showing sin B over b equals sin A over a

Step#3: Plug the values:

Sine Rule example with sin B over 14 equals sin 45 degrees over 10

Step#4: Solve for the missing angle:

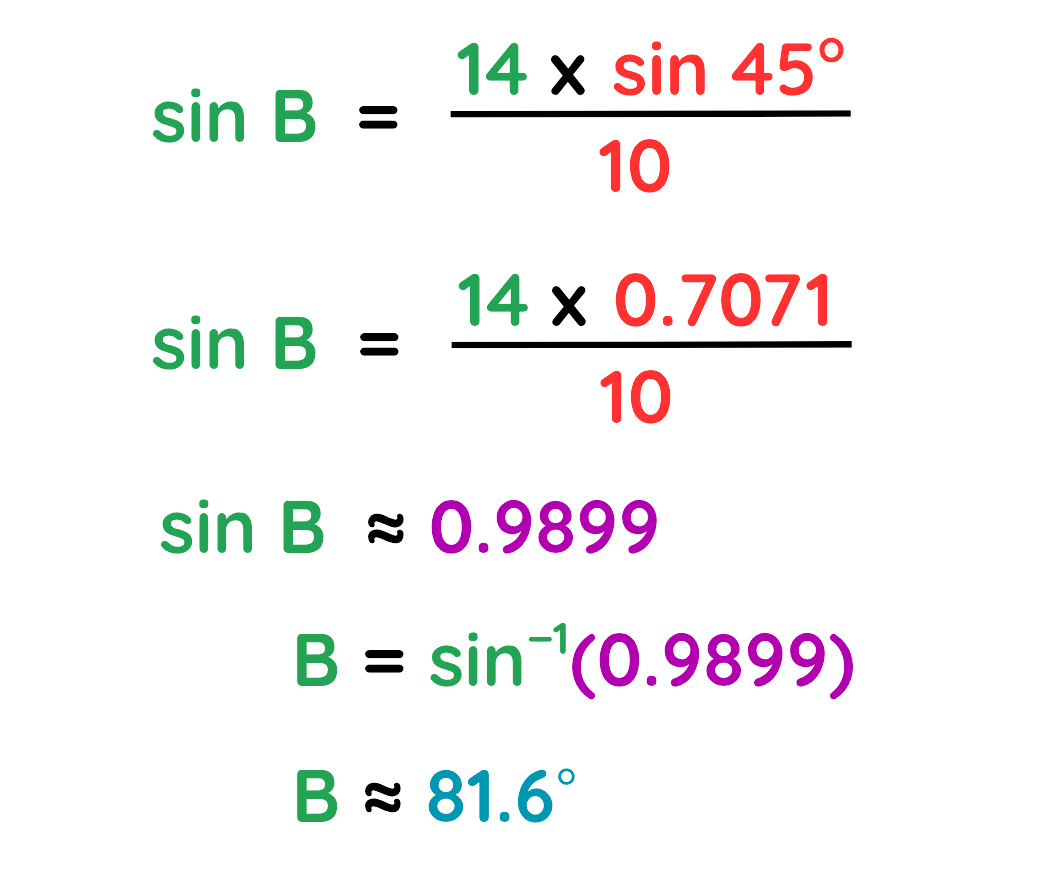
Sine Rule calculation showing steps to find angle B using sin B = 14 times sin 45 divided by 10

The Missing angle of B ≈ 81.6°

Final Answer: B ≈ 81.6°

certified Physics and Maths tutorSolved Example

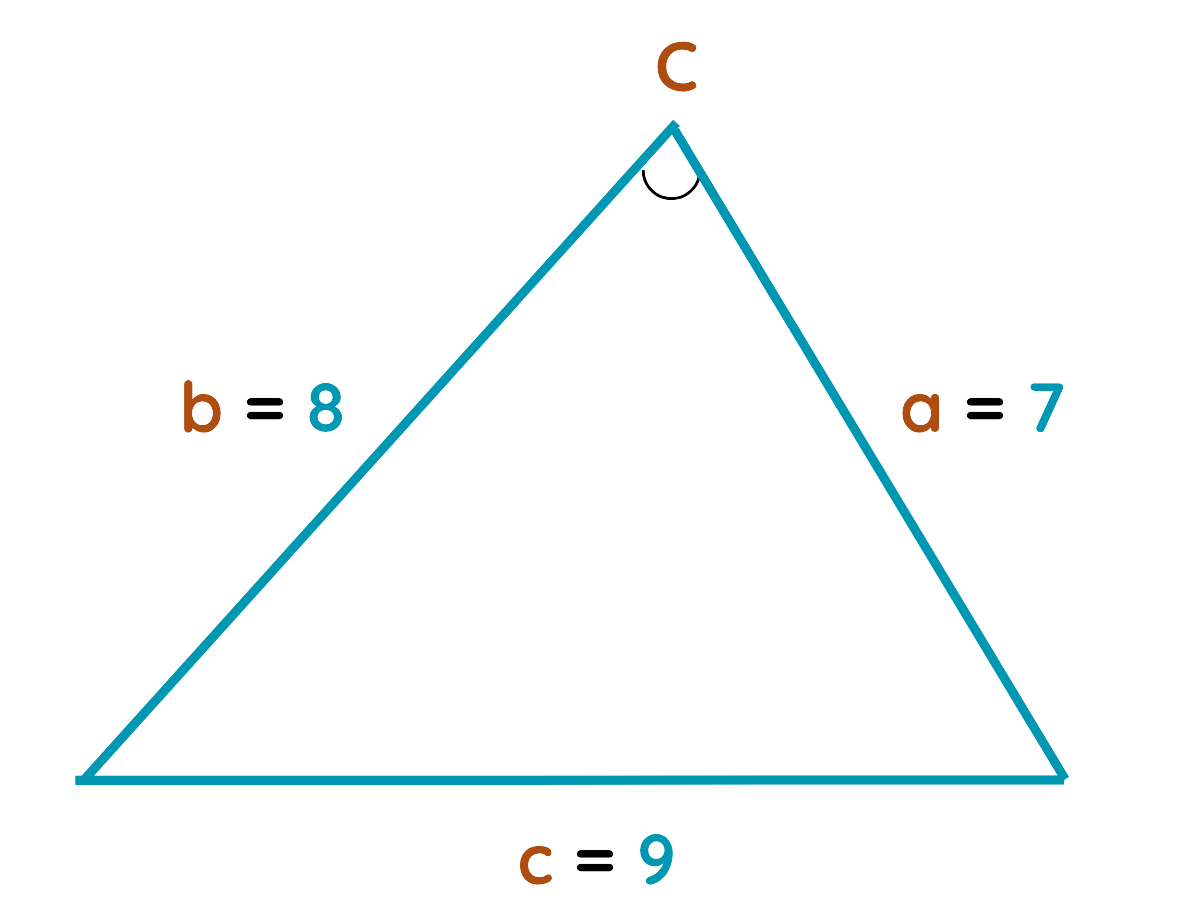
Problem: In Triangle ABC, Side a = 7cm, Side b = 8cm and Side c = 9cm. Find angle C.

Triangle with sides a = 7, b = 8, and c = 9 for Cosine Rule calculation

Solution: 

Step#1: Given:

    • Side a = 7cm
    • Side b = 8cm
    • Side c = 9cm

Step#2: Use The Formula:

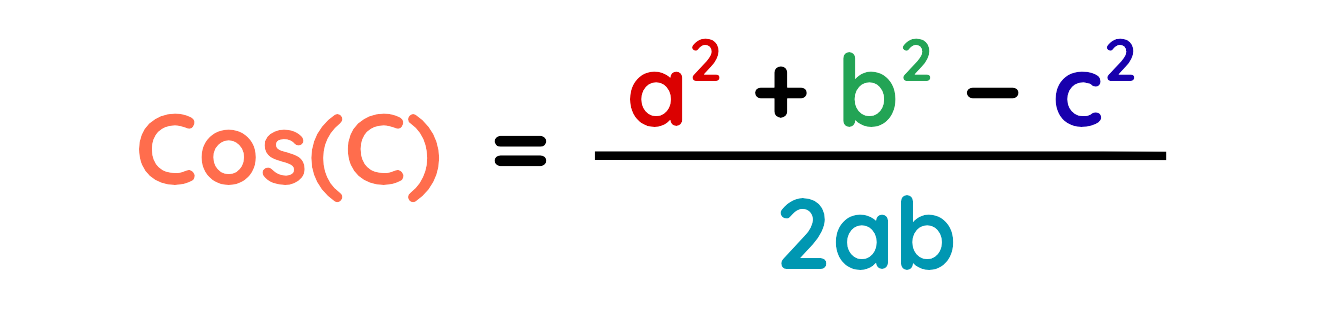
Step#3: Plug the values:

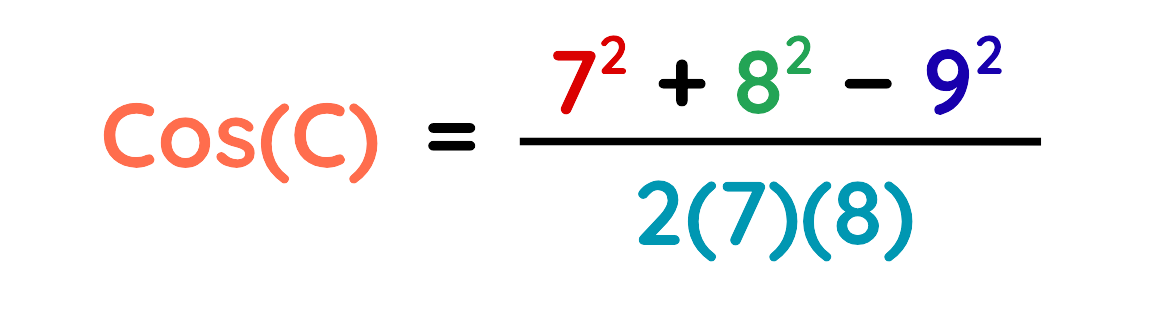
Cosine Rule formula with numbers substituted to calculate angle C

Step#4: Solve for the missing angle:

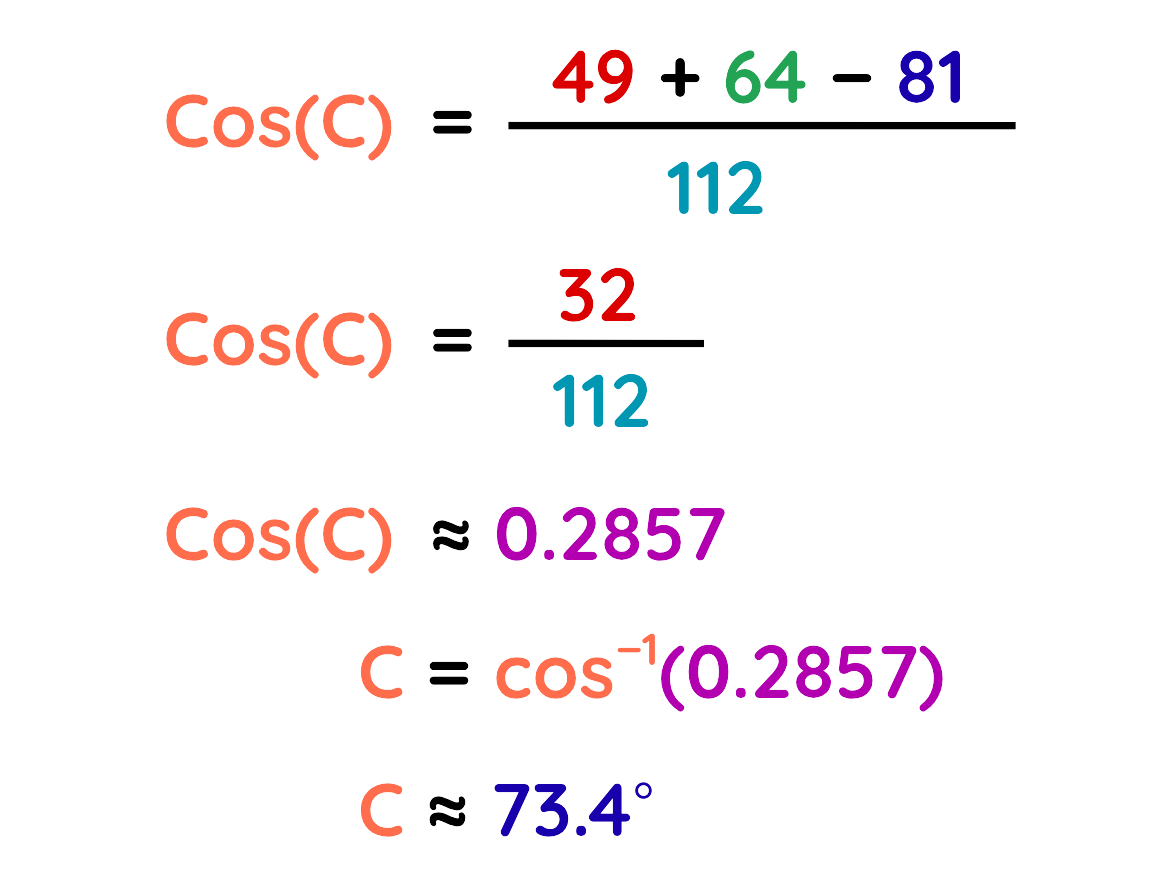
Worked solution using Cosine Rule to find angle C with calculation steps

The Missing angle of C ≈ 73.4°

Final Answer: C ≈ 73.4°

certified Physics and Maths tutorSolved Example

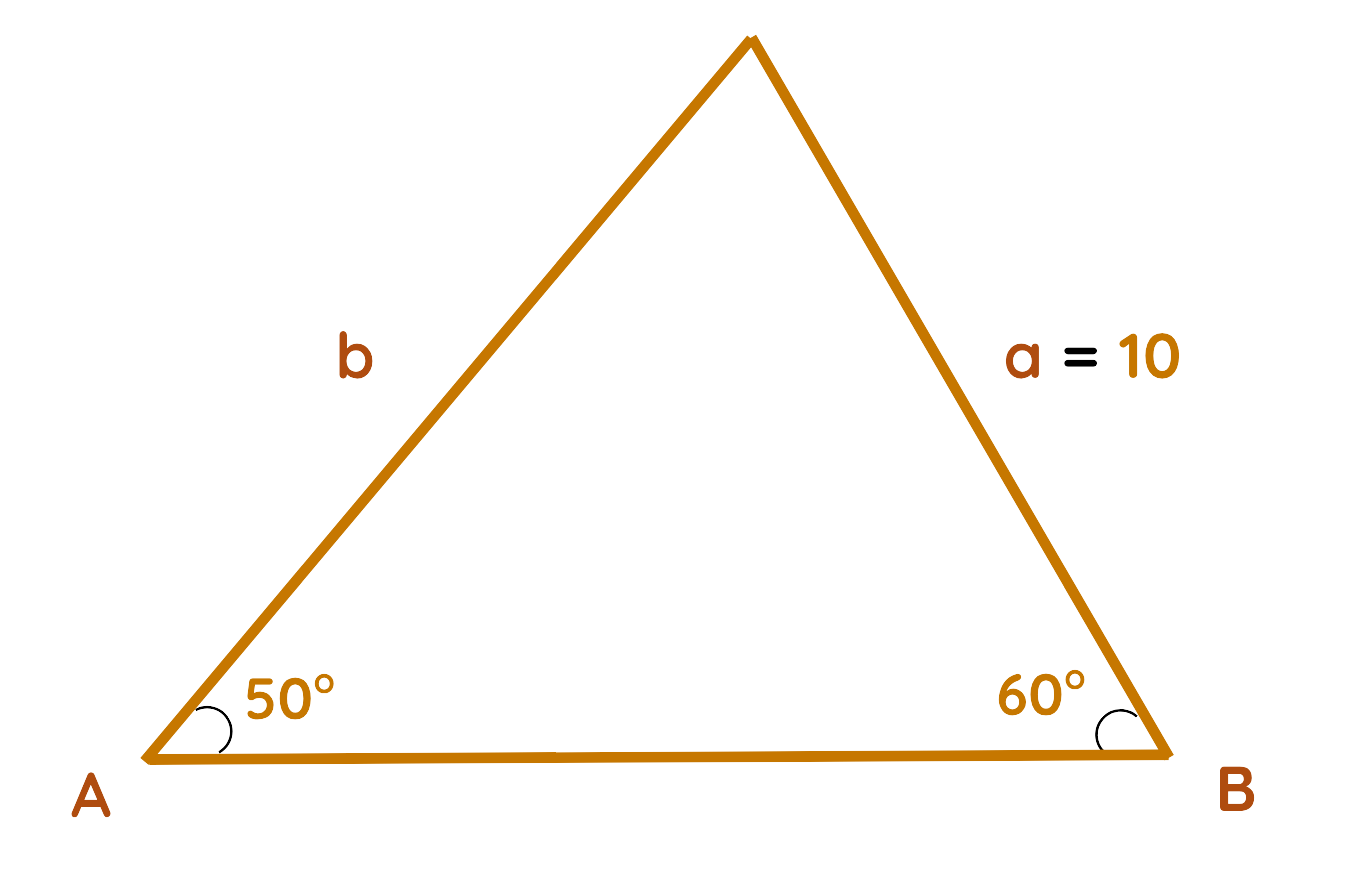
Problem: In Triangle ABC, Angle A = 50°, Angle B = 60° and Side a = 10cm. Find side b.

Triangle with angles 50 degrees and 60 degrees and side a = 10 cm labelled for Sine Rule

Solution: 

Step#1: Given:

    • Side a = 10cm
    • Angle A = 50°
    • Angle B = 60°

Step#2: Use The Formula:

Law of Sine rearrangement to calculate unknown side b using angles and side a

Step#3: Plug the values:

Sine Rule equation showing 10 over sin 50 equals b over sin 60

Step#4: Solve for the missing Side:

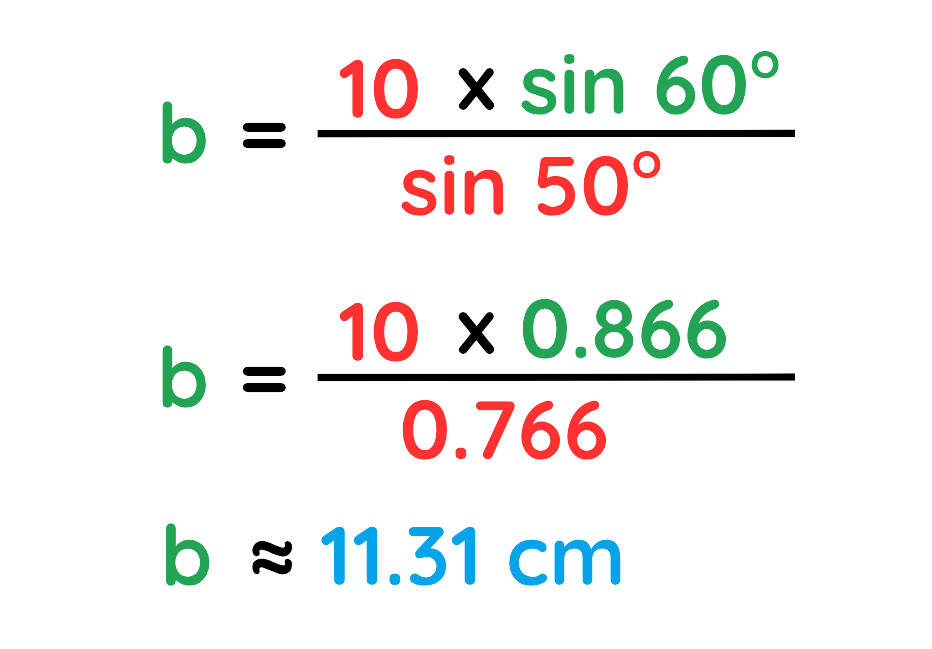
Sine Rule calculation steps showing b equals 10 times sin 60 divided by sin 50 equals 11.31 cm

The Missing side of b ≈ 11.31 cm

Final Answer: b ≈ 11.31 cm

Table of Content

Join Tutoring