Law of Indices Rules | GCSE Maths
Understanding Indices
Indices, also known as exponents or powers, provide a way to represent repeated multiplication in a simpler form.
For example:
Instead of writing 2 × 2 × 2 × 2 × 2, we write 2⁵.
Here, 2 is the base, and 5 is the index (or exponent), meaning the base is multiplied five times.
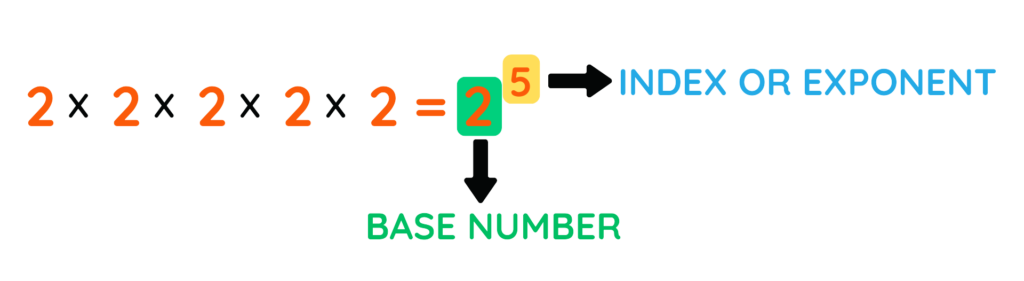
Similarly, 5 × 5 × 5 can be written as 5³, meaning 5 multiplied by itself three times.

To simplify mathematical expressions involving exponents, we use specific rules called the Laws of Indices.
Laws of Indices
1. Multiplication Rule
- Rule: When multiplying numbers with the same base, add the indices.

Example:
Question: Simplify: 23 × 24
Solution:
- Step #1: Expand the Powers
(2 × 2 × 2) × (2 × 2 × 2 × 2) = 27
- Step #2: Apply the Multiplication Rule:
am × an = am + n
23 × 24 = 23 + 4 = 27
2. Division Rule
- Rule: When dividing numbers with the same base, subtract the indices.

Example:
Question: Simplify: 75 ÷ 72
Solution:
- Step #1: Expand the Powers
(7 × 7 × 7 × 7 × 7) ÷ (7 × 7) = 73
- Step #2: Apply the Division Rule:
am ÷ an = am – n
75 ÷ 72 = 75 – 2 = 73
3. Power of a Power Rule
- Rule: When raising a power to another power, multiply the indices.

Example:
Question: Simplify: (34)2
Solution:
- Step #1: Expand the Expression
(3 × 3 × 3 × 3) × (3 × 3 × 3 × 3)
- Step #2: Apply the Power Rule:
(am)n = am × n
(34)2 = 34 × 2 = 38
4. Zero Index Rule
- Rule: Any number raised to the power of zero is always equal to 1.

Example:
- 50 = 1
5. Negative Index Rule
- Rule: A negative exponent means the reciprocal of the base with a positive exponent.
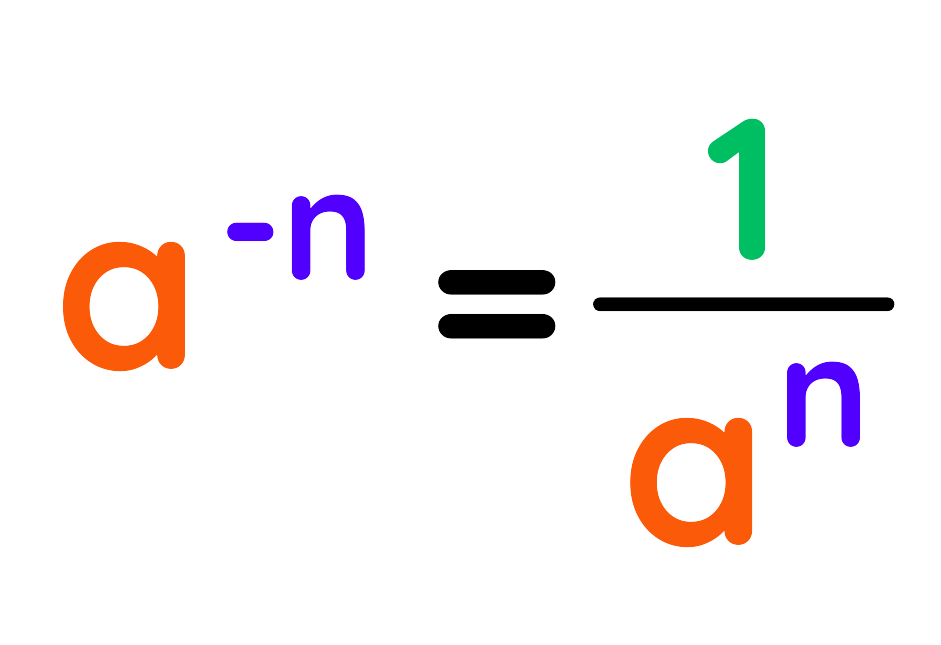
Example:
Question: Simplify: 2-3
Solution:
- Step #1: Apply the Negative Index Rule
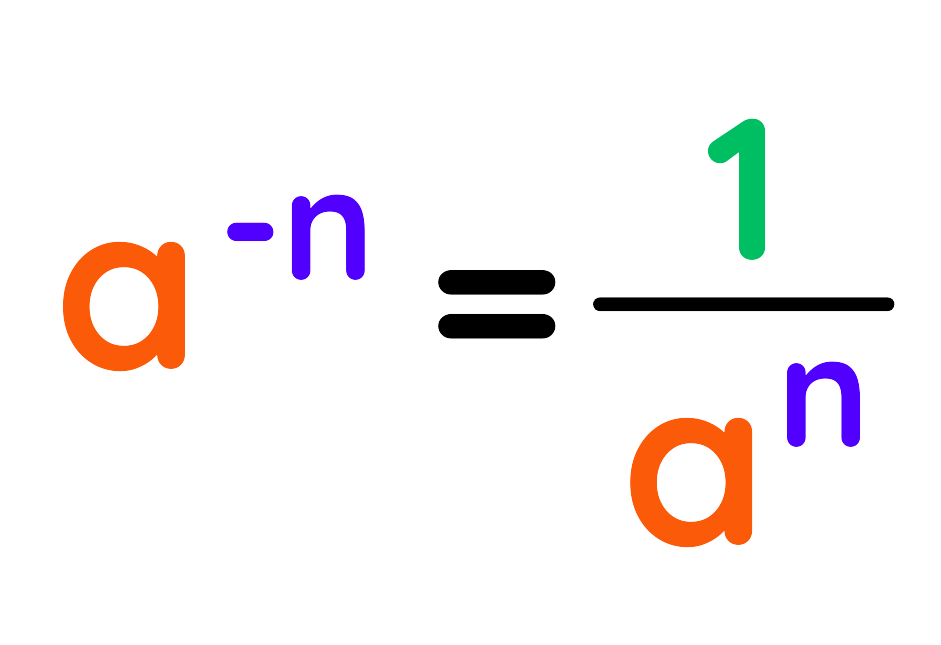
2-3 = 1 / 23
- Step #2: Expand the Power:
23 = 2 × 2 × 2 = 8
2-3 = 1/8
6. Fractional Index Rule (GCSE Higher Maths)
- Rule: A fractional exponent represents a root.

📌 This is a GCSE Higher Maths topic. To learn more about it, click on this link: Fractional Indices
Example 1:
Question: Simplify: 16{1/2}
Solution:
- Step #1: Understand the Fractional Exponent Rule
16{1/2} = √16
- Step #2: Find the Square Root
√16 = 4
Example 2:
Question: Simplify: 27{1/3}
Solution:
- Step #1: Understand the Fractional Exponent Rule
27{1/3} = ³√27
- Step #2: Find the Square Root
³√27 = 3
 Solved Example
Solved Example
Problem: Simplify:
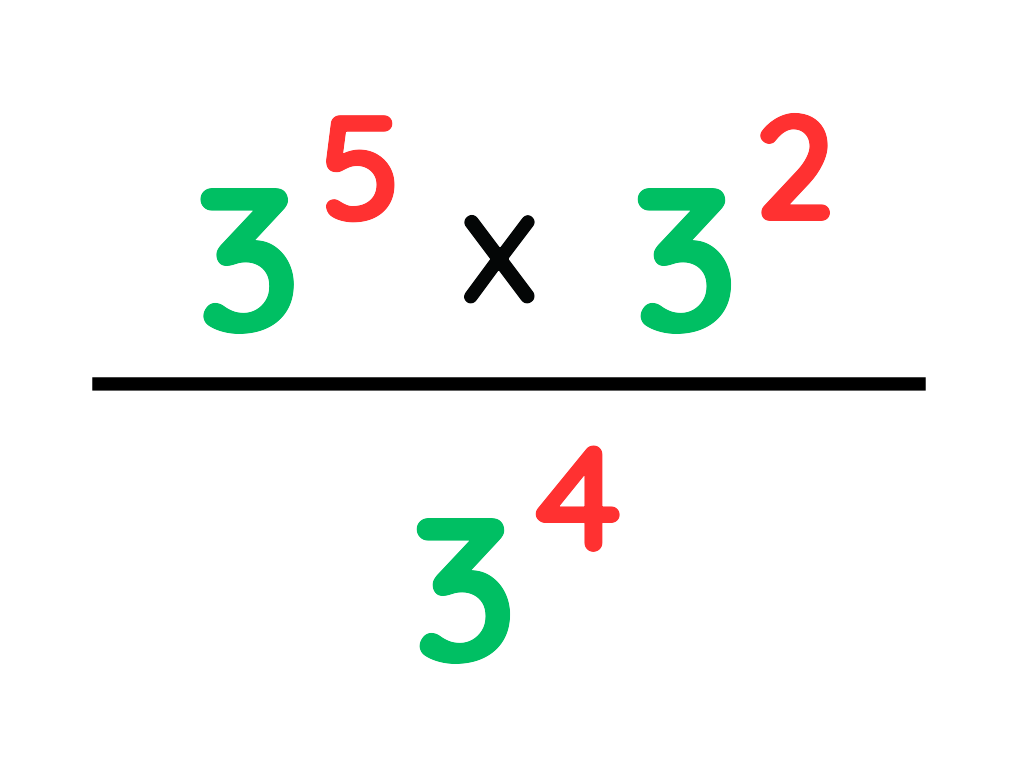
Solution:
Step #1: Apply the multiplication rule to the numerator:

Step #2: Apply the division rule:

Final Answer: 33
 Solved Example
Solved Example
Problem: Simplify:
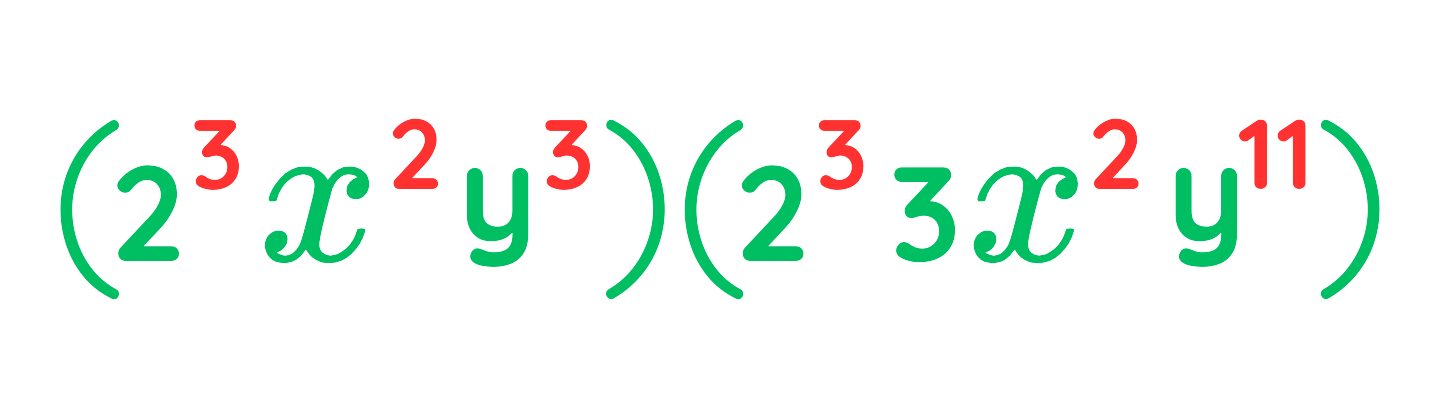
Solution:
Step #1: Group terms with the same base:
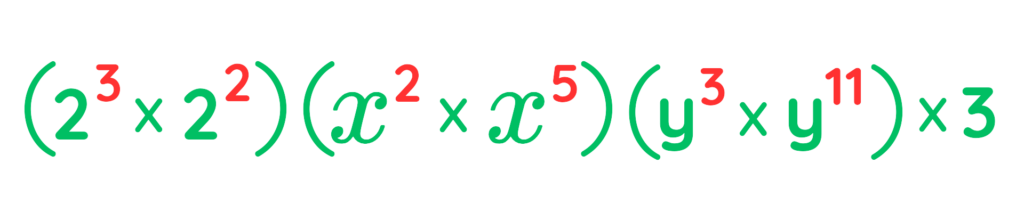
Step #2: Apply the multiplication rule to each base:

Final Answer:
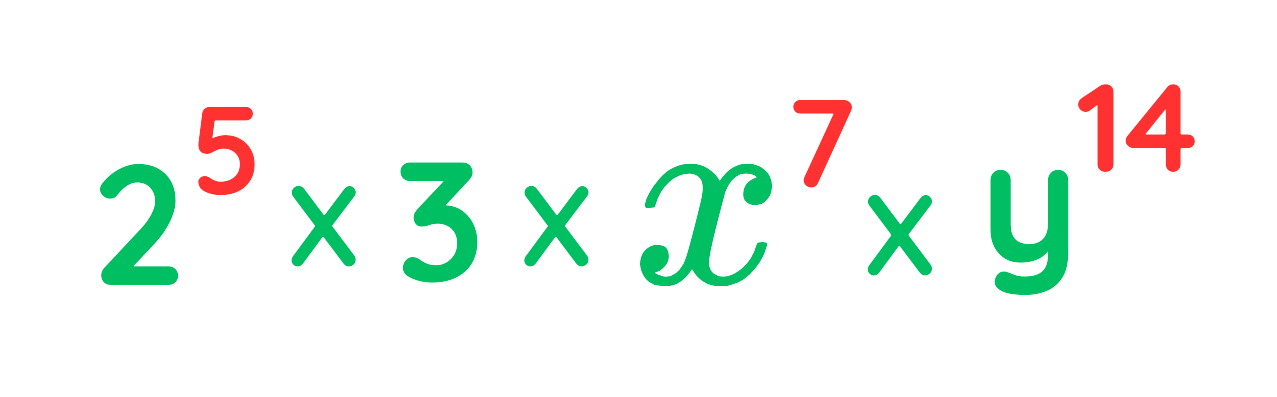
 Solved Example
Solved Example
Problem: Simplify:
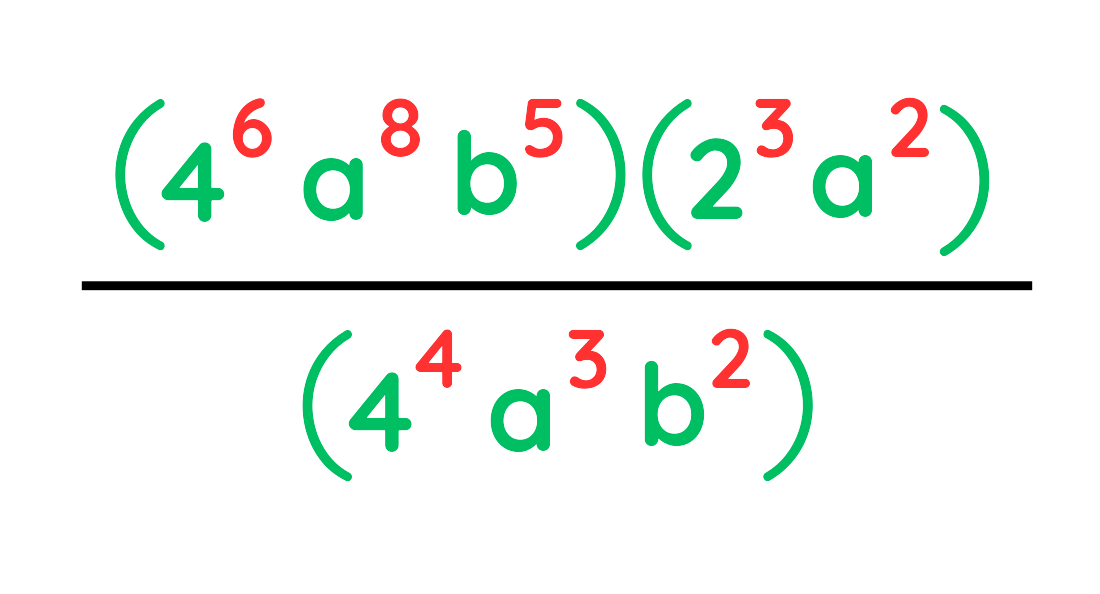
Solution:
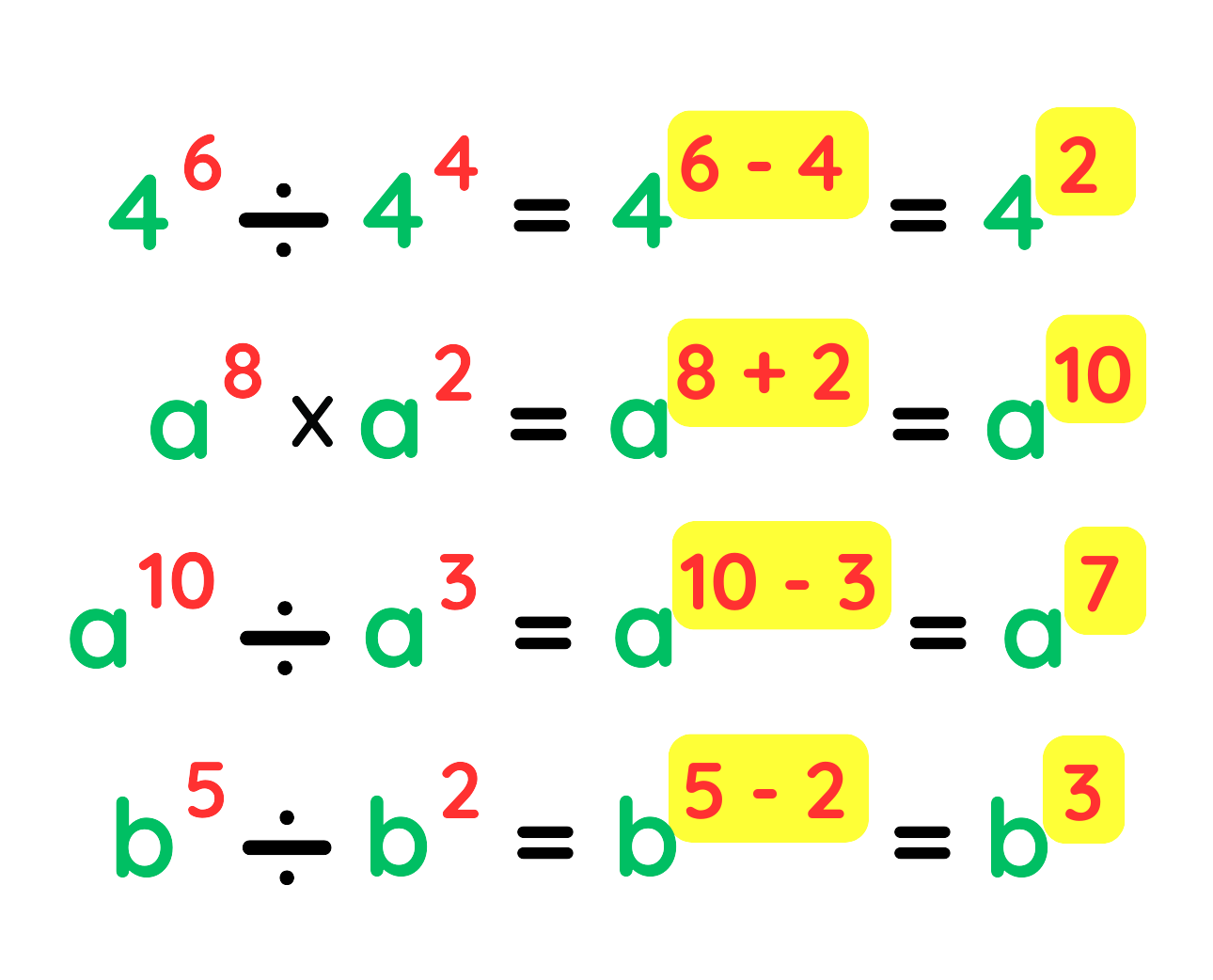
Step #1: Group terms:
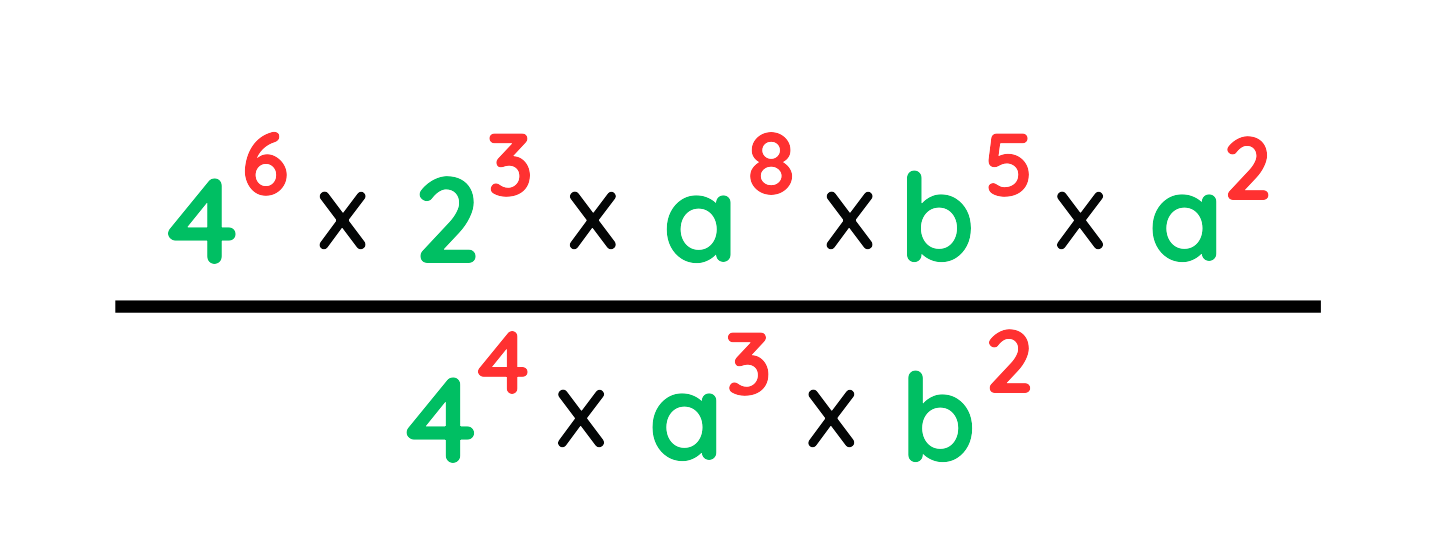
Step #2: Apply multiplication and division rules:
Step #3: Convert 42 into base 2:
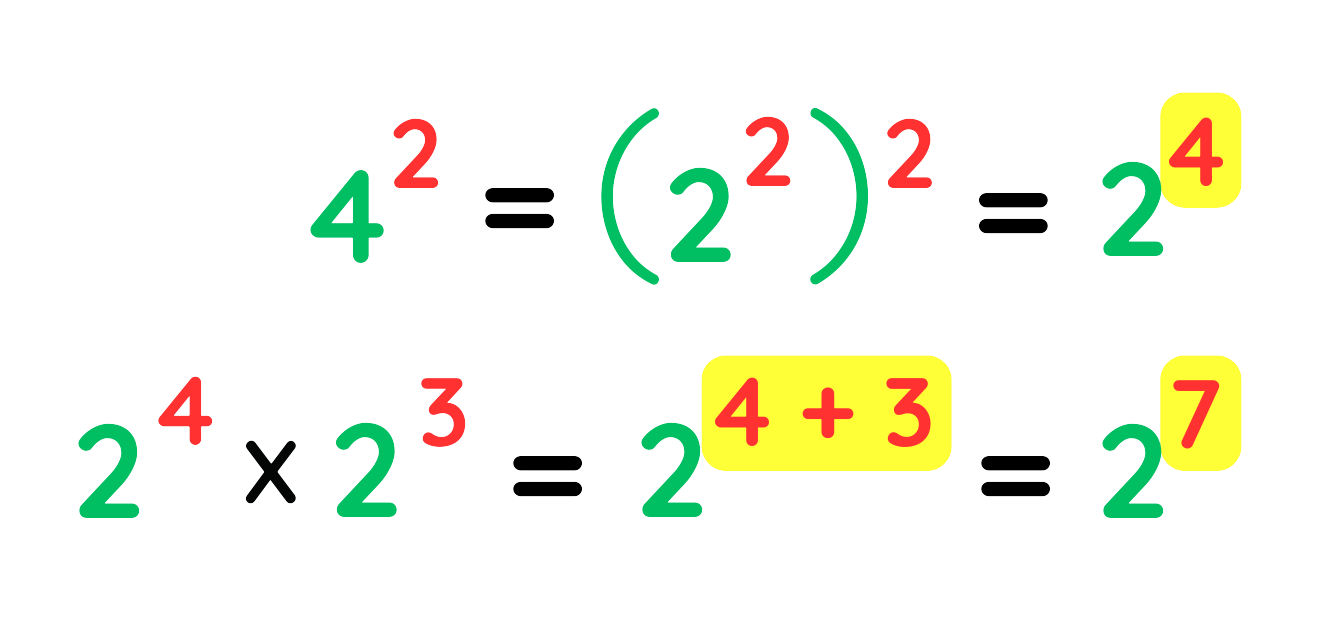
Final Answer:

Practice Questions and Answers on Law of Indices
Question 1:
(a) Simplify x⁸ × x³
(b) Simplify (5y)³
(c) Simplify w⁷ ÷ w⁴
Question 2:
(a) Simplify a⁹ × a⁴
(b) Simplify (4b²c)³
(c) Simplify d⁹ ÷ d⁴
Question 3:
(a) Simplify 2m² × 5n⁶
(b) Simplify 15p³ ÷ 3p⁴
Question 4:
(a) Simplify (t³)⁴
(b) Simplify 12m²n⁶ ÷ 3mn⁴
Question 5:
(a) Given y² × yᵃ = y⁷,find the value of a.
(b) Given (y⁴)ᵇ = y¹², find the value of b.
Question 6:
(a) Given x⁶ ÷ xᵃ = x⁸, find the value of a.
(b) Simplify (2m²)⁴.
Question 7:
(a) Write (3⁴ × 3⁵) ÷ 3² as a power of 3.
(b) Write down the value of 3⁻³.
(c) Write down the value of 3⁰.
Question 8:
(a) Simplify p³ × p⁵.
(b) Simplify (4ab²)³.
(c) Simplify 16m⁷n³ ÷ 4m³n.
Question 9: Work out the value of (2³ × 2) ÷ 2⁵.
Question 10:
(a) Simplify 9p³ × 2p⁻².
(b) Simplify (5x³y²)³.
(c) Given p³ × p⁵ = p¹² × pʸ, find the value of y.
Solutions
Question 1:
Solution:
(a) x¹¹
(b) 125y³
(c) w³
Question 2:
Solution:
(a) a¹³
(b) 14
(c) d⁵
Question 3:
Solution:
(a) 10m²n⁶
(b) 5p⁻¹
Question 4:
Solution:
(a) t¹²
(b) 15m³n⁷
Question 5:
Solution:
(a) 5
(b) 3
Question 6:
Solution:
(a) -2
(b) 16m⁸
Question 7:
Solution:
(a) 3⁷
(b) 1/27
(c) 1
Question 8:
Solution:
(a) p⁸
(b) 64a³b⁶
(c) 4m⁴n²
Question 9:
Solution: 1/2
Question 10:
Solution:
(a) 10c²d⁴
(b) 125x⁹y⁶
(c) -4

