Independent Events – GCSE Maths
Introduction
- In Probability Theory, Independent events are the important concepts that describe different relationships between events.
- It describes how the occurrence of one event affects the probability of another event.
What are Independent Events?
- Two events are Independent if one event does not affect the probability of the other.
- For example: Flipping heads with a coin has no effect on rolling an even number with some dice, so they are Independent events.
- If the occurrence of one does affect the probability of the other, then it is called Dependent Events.
- Mathematically,
Steps To Solve The Independent Events
- To determine whether two events are independent and calculate their probabilities, follow these steps:
Steps To Solve:
- Step#1: Identify Events
- Step#2: Use Formula
- Step#3: Calculate the Probability
Solved Example
Solved ExampleProblem: If we flip a fair coin and roll a fair 6-sided die. What’s the probability of getting Tails on the coin and an even number on the die?
Solution:
Step#1: Identify Events:
- Event A: Coin lands Tails: P(A) = 1/2
- Event B: Die shows even number (2, 4 and 6): P(B) = 3/6 = 1/2
Step#2: Use Formula:
Step#3: Calculate the Probability:
Put the Values in formula,
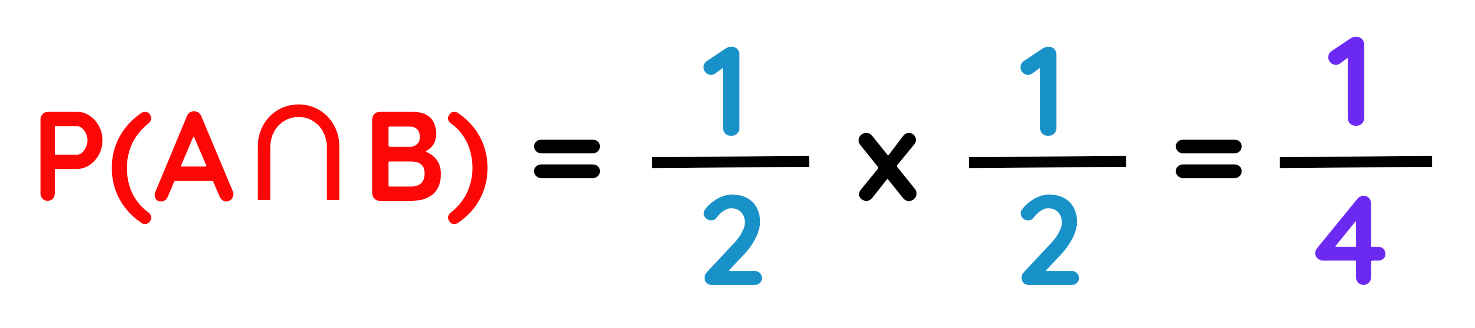
Final Answer: 1/4
Solved Example
Problem: A coin is tossed and a die is rolled. What is the probability of getting Heads on the coin and a 4 on the die?
Solution:
Step#1: Identify Events:
- Event A: Getting Heads on the coin: P(A) = 1/2
- Event B: Getting a 4 on the die: P(B) = 1/6
Step#2: Use Formula:
Step#3: Calculate the Probability:
Put the Values in formula,
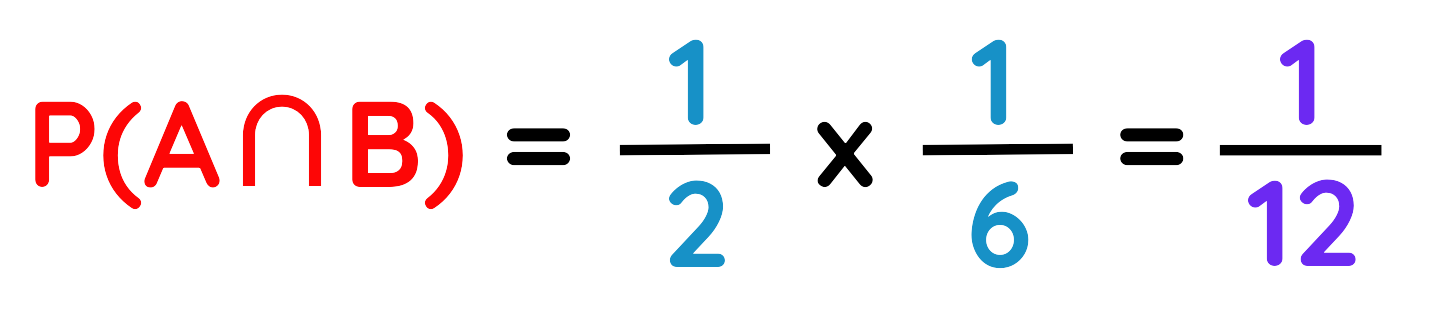
Final Answer: 1/12
Solved Example
Problem: A bag contains 3 red marbles and 2 blue marbles. You randomly pick a marble, put it back, and then draw again. What is the probability of getting:
- A red marble first
- A blue marble second
Solution:
Step#1: Identify Events:
Total marbles = 3 red + 2 blue = 5 marbles.
- Event A: First draw is red: P(A) = 3/5
- Event B: Second Draw is Blue: P(B) = 2/5
Step#2: Use Formula:
Step#3: Calculate the Probability:
Put the Values in formula,
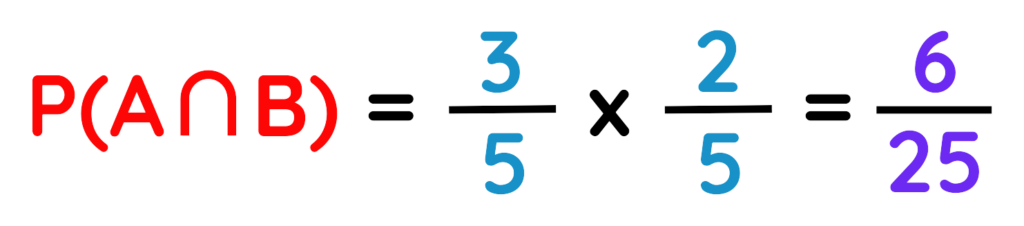
Final Answer: 6/25
Solved Example
Problem: A restaurant serves pizza with 3 topping choices: Pepperoni (P), Mushrooms (M), and Olives (O). Each topping has an independent probability of being selected by a customer:
What is the probability that a customer orders a pizza with both Pepperoni and Mushrooms.
Solution:
Step#1: Identify Events:
- Event A: Customer selects Pepperoni: P(A) = 0.6
- Event B: Customer selects Mushrooms: P(B) = 0.4
Step#2: Use Formula:
Step#3: Calculate the Probability:
Put the Values in formula,
Final Answer: 0.24
Solved Example
Problem: If roll a fair 6-sided die twice, what is the probability of getting a 5 on the first roll and a 2 on the second roll?
Solution:
Step#1: Identify Events:
- Event A: First die roll: P(5) = 1/6
- Event B: Second die roll: P(2) = 1/6
Step#2: Use Formula:
Step#3: Calculate the Probability:
Put the Values in formula,
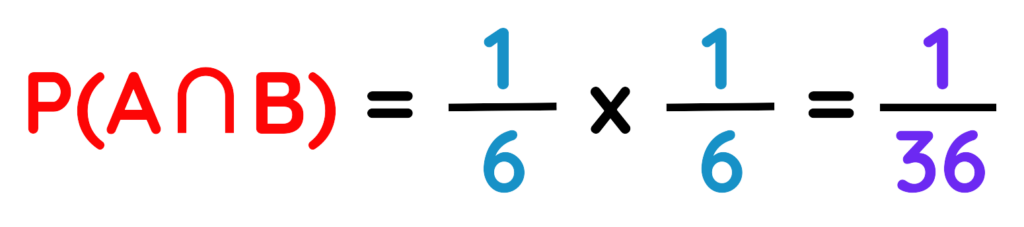
Final Answer: 1/36