Calculate Area Using Sine Rule​ – GCSE Maths

Practice Questions
Downloads

Introduction

  • Law of Sines are trigonometric formulas used to solve any triangles when certain information is given.
  • This law is used to find unknown sides or angles in non-right-angled triangles, it can also be applied to calculate the area of a triangle when certain information is given.
  • It is a fundamental tool used to solve real-world problems involving triangles.

What is the Sine Rule?

  • The Sine Rule states that, in any triangle, the ratio of the length of a side to the sine of its opposite angle is the same for all three sides.
  • The Sine Law is expressed as:

For any triangle with sides a, b and c opposite angles A, B and C respectively, for finding missing side:

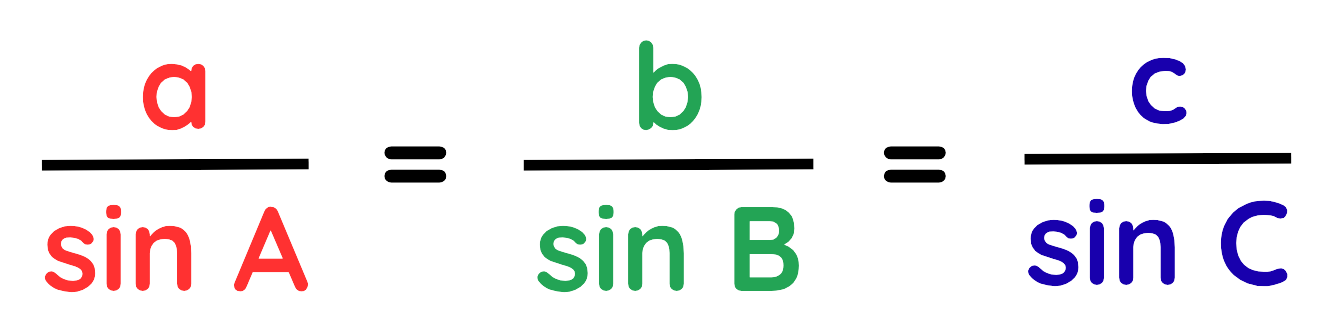
Sine Rule for Calculating the Area of a Triangle

  • The Sine Rule is not just used for solving sides and angles, but it is also helpful to calculate the area of triangle especially when height is unknown.
  • Mathematically,
    • For any triangle with sides a, b, c and opposite angles A, B and C:

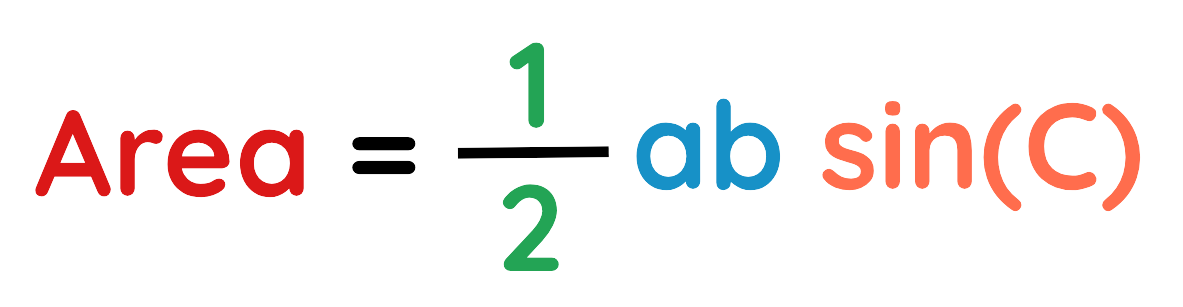
Where:

    • a and b are two known sides.
    • C is the angle between them (included angle).

It can also use as:

Triangle area formula half bc sin A or half ac sin B using sine rule

certified Physics and Maths tutorSolved Example

Problem: A triangle has sides a = 9cm, b = 6cm, and the included angle C = 62∘. Find its area.

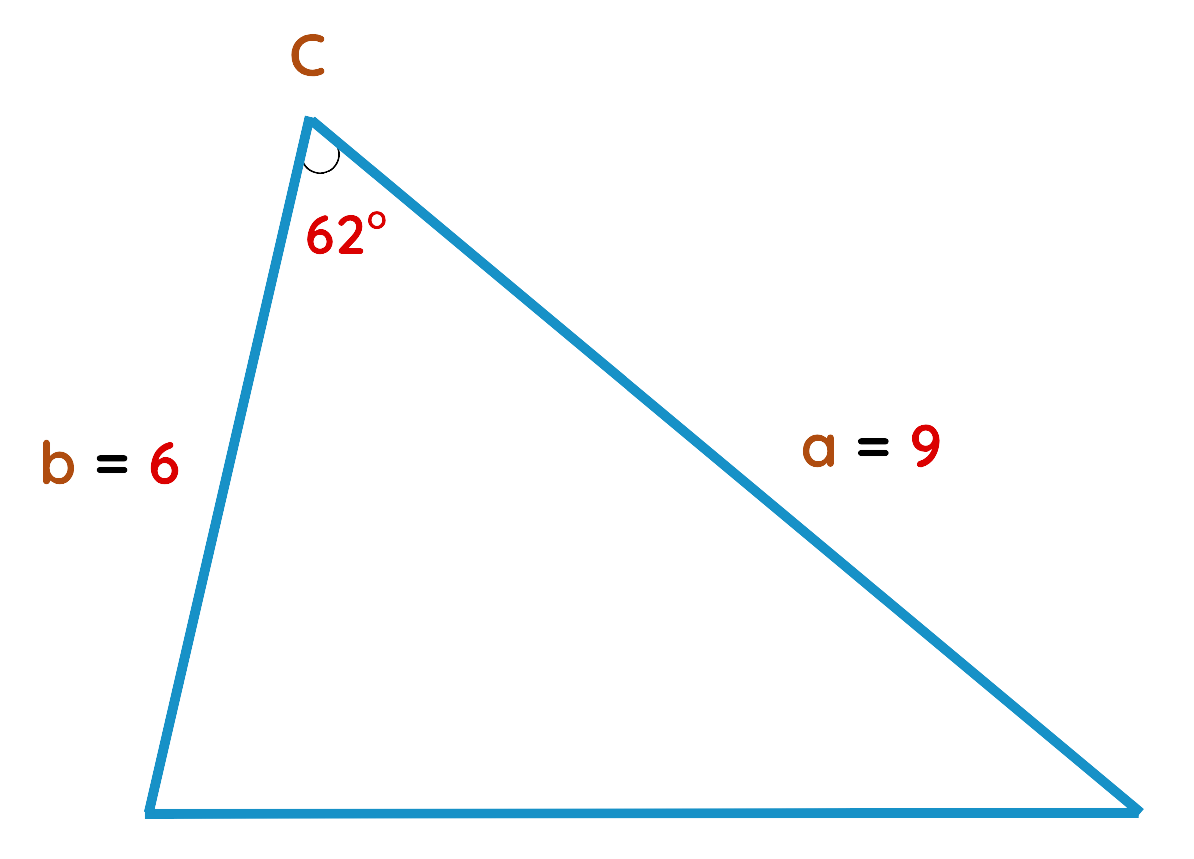
Triangle with sides 9 and 6 and included angle 62 degrees for area calculation using sine rule

Solution: 

Using the formula:

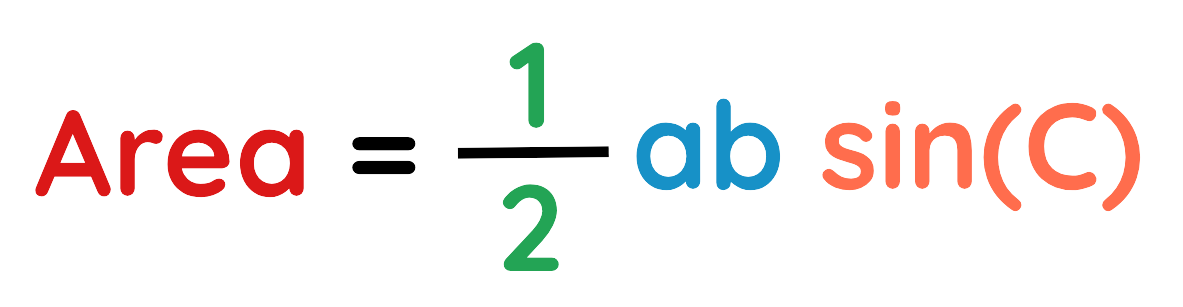
Plug the values and solve:

Solution calculating area of triangle with sides 9 and 6 and included angle 62 degrees using sine rule

Final Answer: 23.8383 cm2

How to Calculate Area of Triangle Using Sine Rule?

  • We can calculate the area of any triangle using the sine rule, based area formula, especially when we know two sides and the included angle between them.

Steps to Calculate The Area of Triangle:

  • Step#1: Identify the known values
  • Step#2: Use the formula based on information.
  • Step#3: Plug the values in the formula.
  • Step#4: Calculate the area

certified Physics and Maths tutorSolved Example

Problem: In Triangle ABC, side AB = 11 cm, side AC = 8 cm and the angle between them ∠A = 50°.Find the area of triangle ABC.

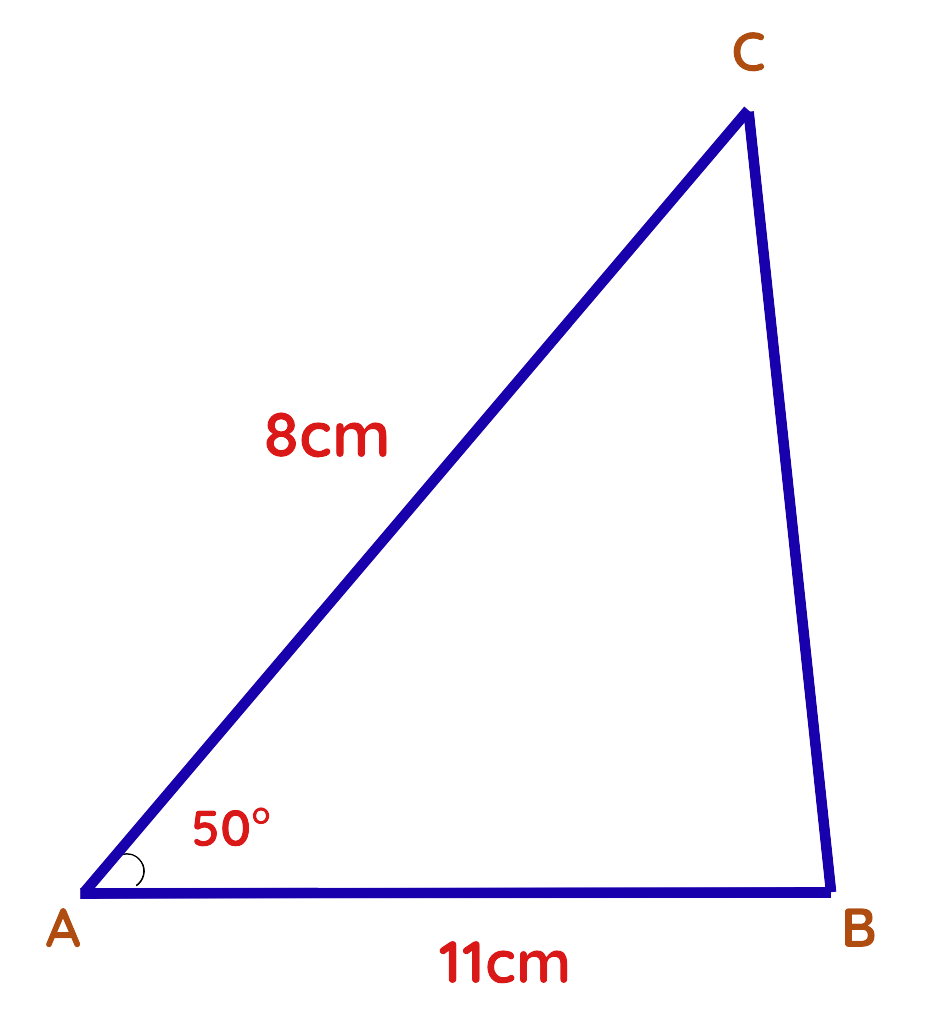
Triangle with sides 8 cm and 11 cm and included angle 50 degrees for area calculation using sine rule

Solution: 

Step#1: Identify the known values:

Given:

    • Side AB = 11 cm
    • Side AC = 8 cm
    • Included angle ∠A = 50°

Step#2: Use The Formula:

Area formula using sine rule showing Area = 1/2 (AB)(AC) sin(A)

Step#3: Plug the values in the formula:

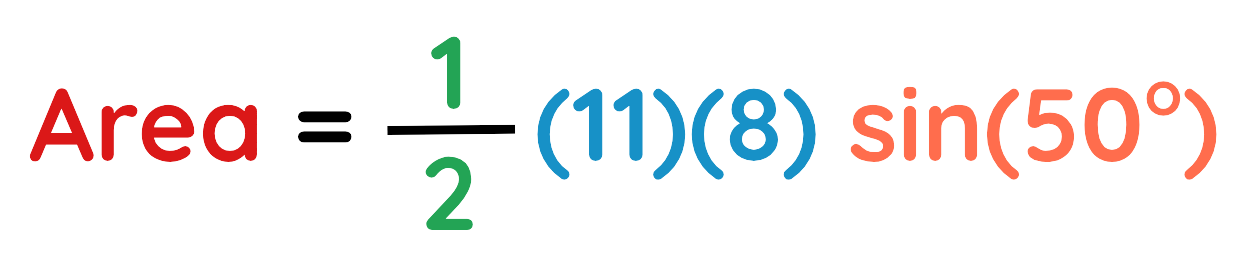
Example calculation of area using sine rule with sides 11 and 8 and included angle 50 degrees

Step#4: Calculate the area:

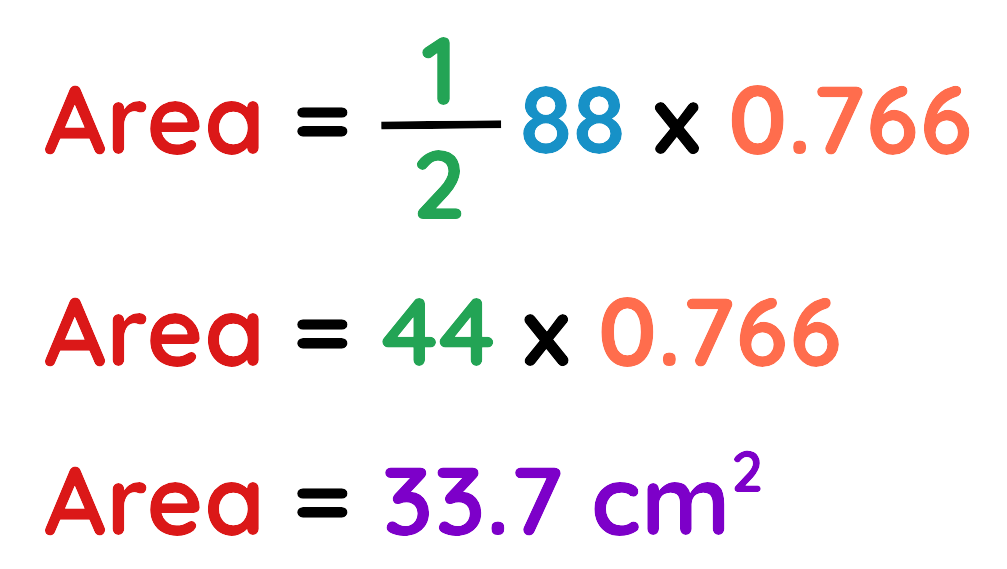
Solution steps for calculating area using sine rule with half times 88 times sin 50 equals 33.7 cm squared

Area of ABC triangle is 33.7cm2.

Final Answer: 33.7cm2

certified Physics and Maths tutorSolved Example

Problem: In Triangle, sides a = 10 cm, side c = 7 cm and the angle B = 40°. Find the area of triangle.

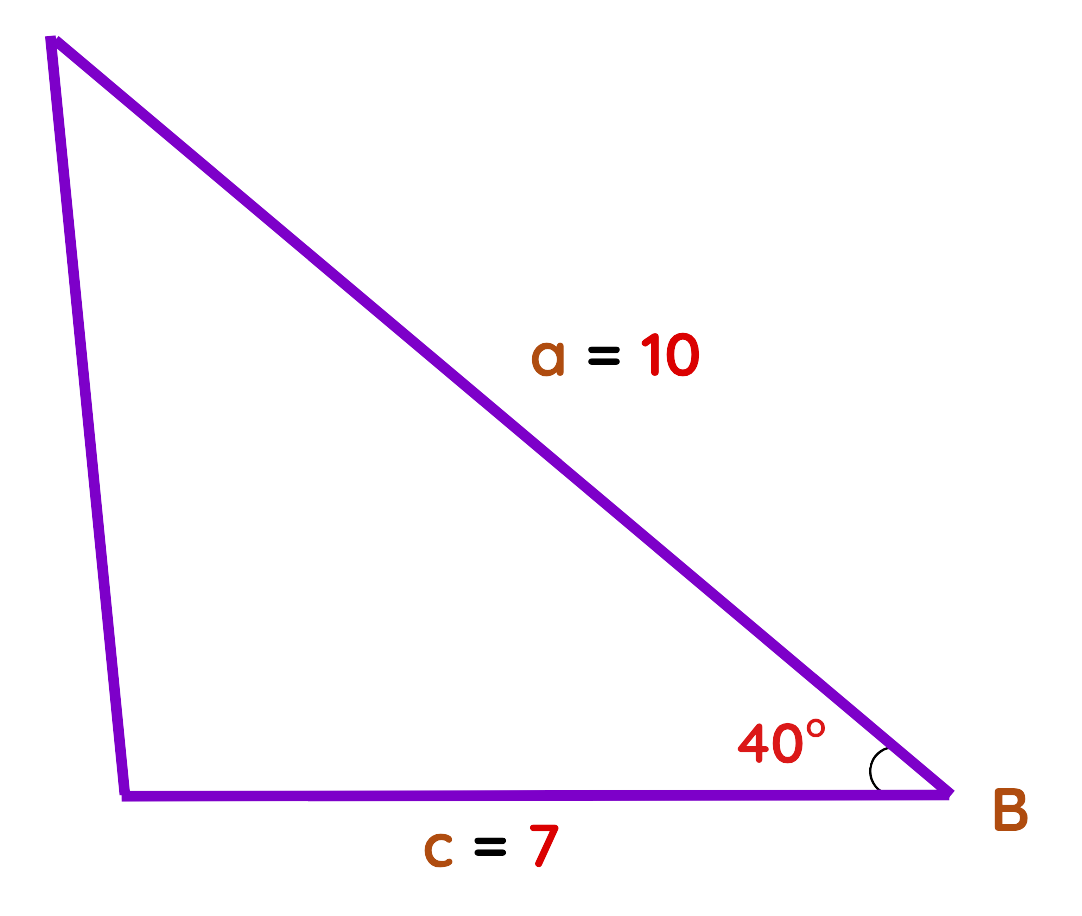
Triangle with sides 10 and 7 and included angle 40 degrees for calculating area using sine rule

Solution: 

Step#1: Identify the known values:

Given:

    • Side A = 10 cm
    • Side C = 7 cm
    • Angle B = 40°

Step#2: Use The Formula:

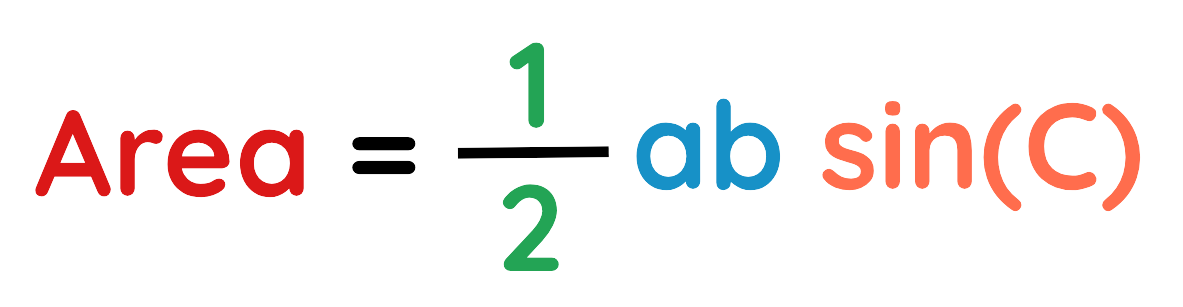
Triangle area formula half ab sin C using sine rule for calculating area

Step#3: Plug the values in the formula:

Area formula using sine rule with sides 10 and 7 and included angle 40 degrees

Step#4: Calculate the area:

Example solution calculating triangle area using sine rule with sides 10 cm and 7 cm and angle 40 degrees

Area of triangle is 22.50 cm2.

Final Answer: 22.50 cm2

certified Physics and Maths tutorSolved Example

Problem: The area of a triangle is 30 cm2. One side a = 6 cm, and the included angle C = 50°. Find the other side b.

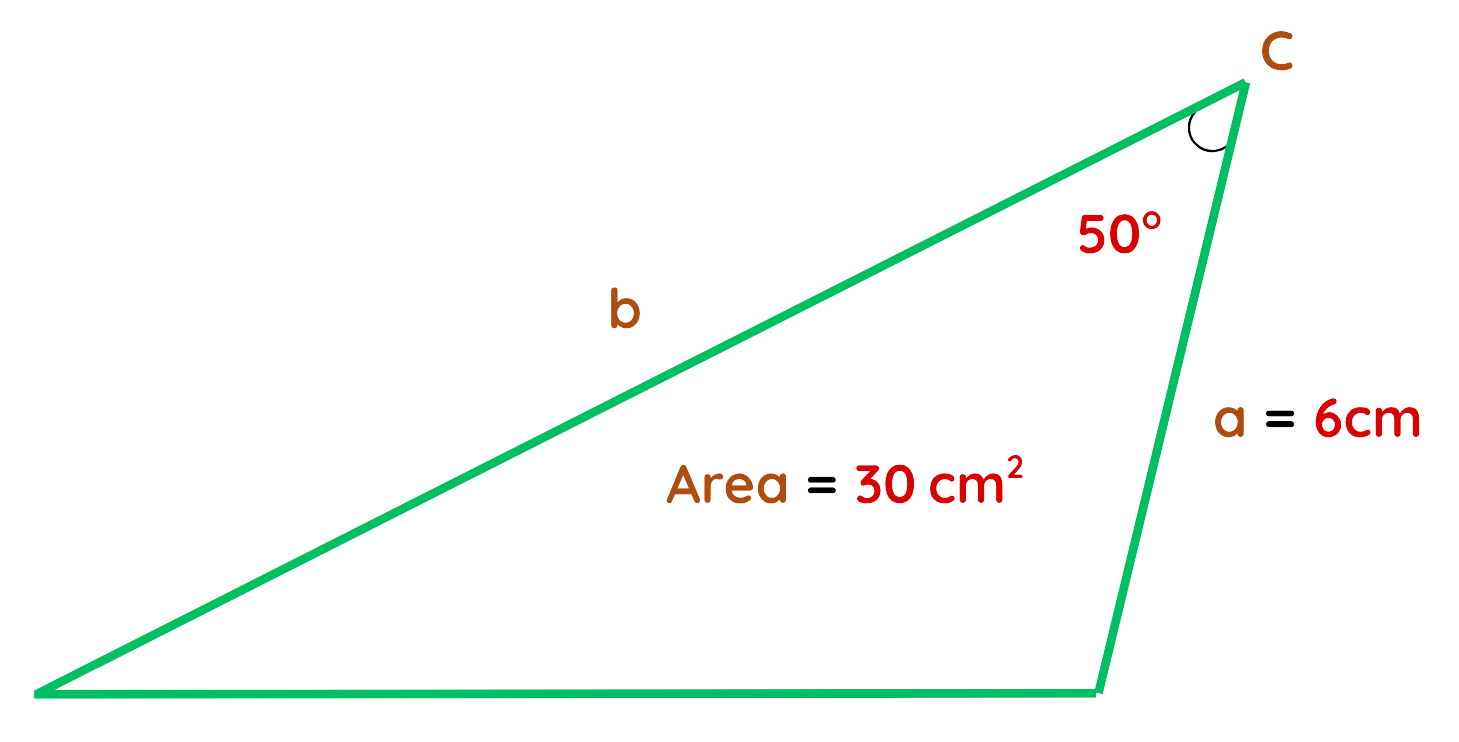
Triangle question showing side a equals 6 cm, angle 50 degrees, and area 30 cm squared to find missing side b

Solution: 

Step#1: Identify the known values:

Given:

    • a = 6 cm
    • Area of Triangle = 30 cm2
    • Angle c = 50°

Step#2: Use The Formula:

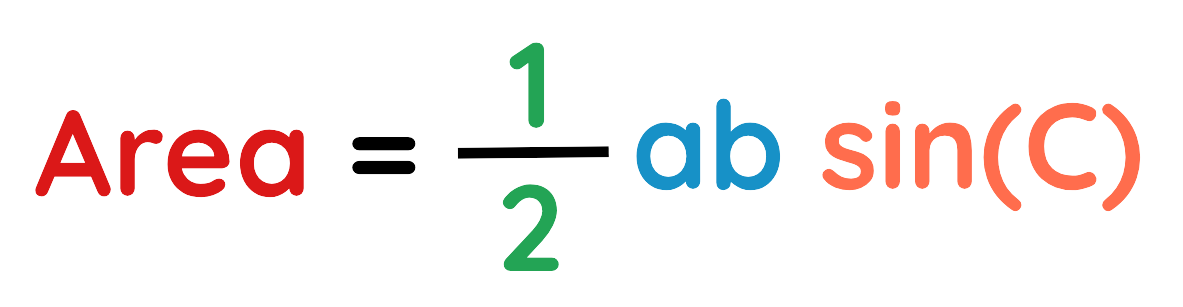
Rearrange it,

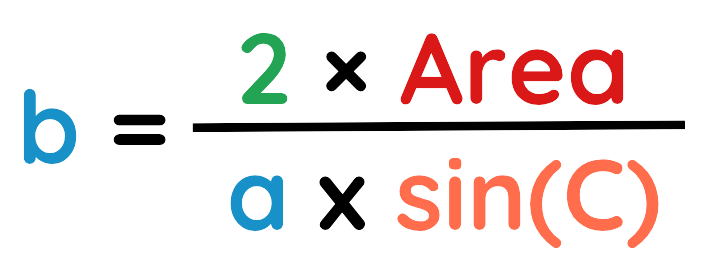
Substitution example calculating missing side using area sine rule formula

Step#3: Plug the values in the formula:

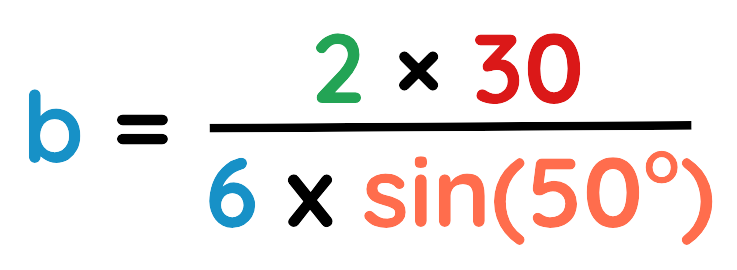
Rearranged formula to find missing side b using area sine rule calculation

Step#4: Calculate the area:

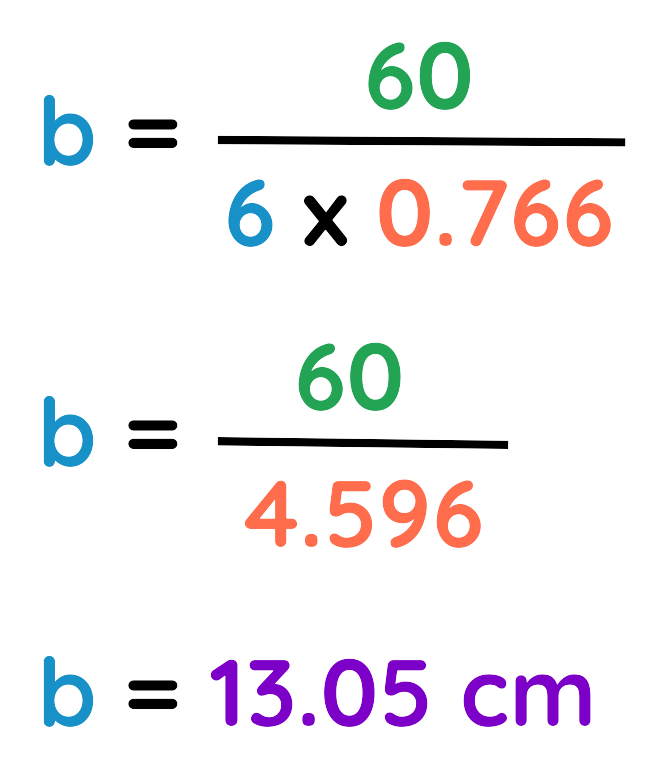
Final calculation of missing side using area sine rule formula example

Final answer is 13.05 cm

Final Answer: 13.05 cm

Table of Content

Join Tutoring