Standard Form – GCSE Maths
Introduction
- Standard Form is a widely accepted way of representing mathematical expressions, numbers, or equations in a clear and structured manner.
What do you mean by Standard Form
- Standard form is a universally recognized way of expressing mathematical concepts with clarity, precision, and consistency.
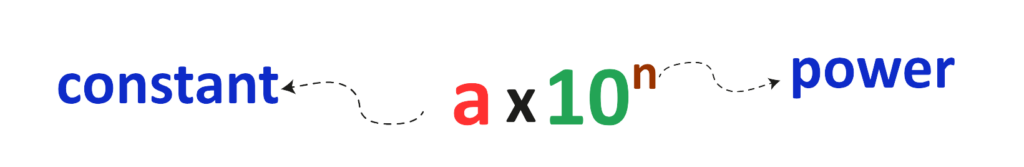
It can be written in the form.
where,
- a is any constant which lies between 1 and 9 i.e {1<a<10}.
- n can be any positive or negative whole number.
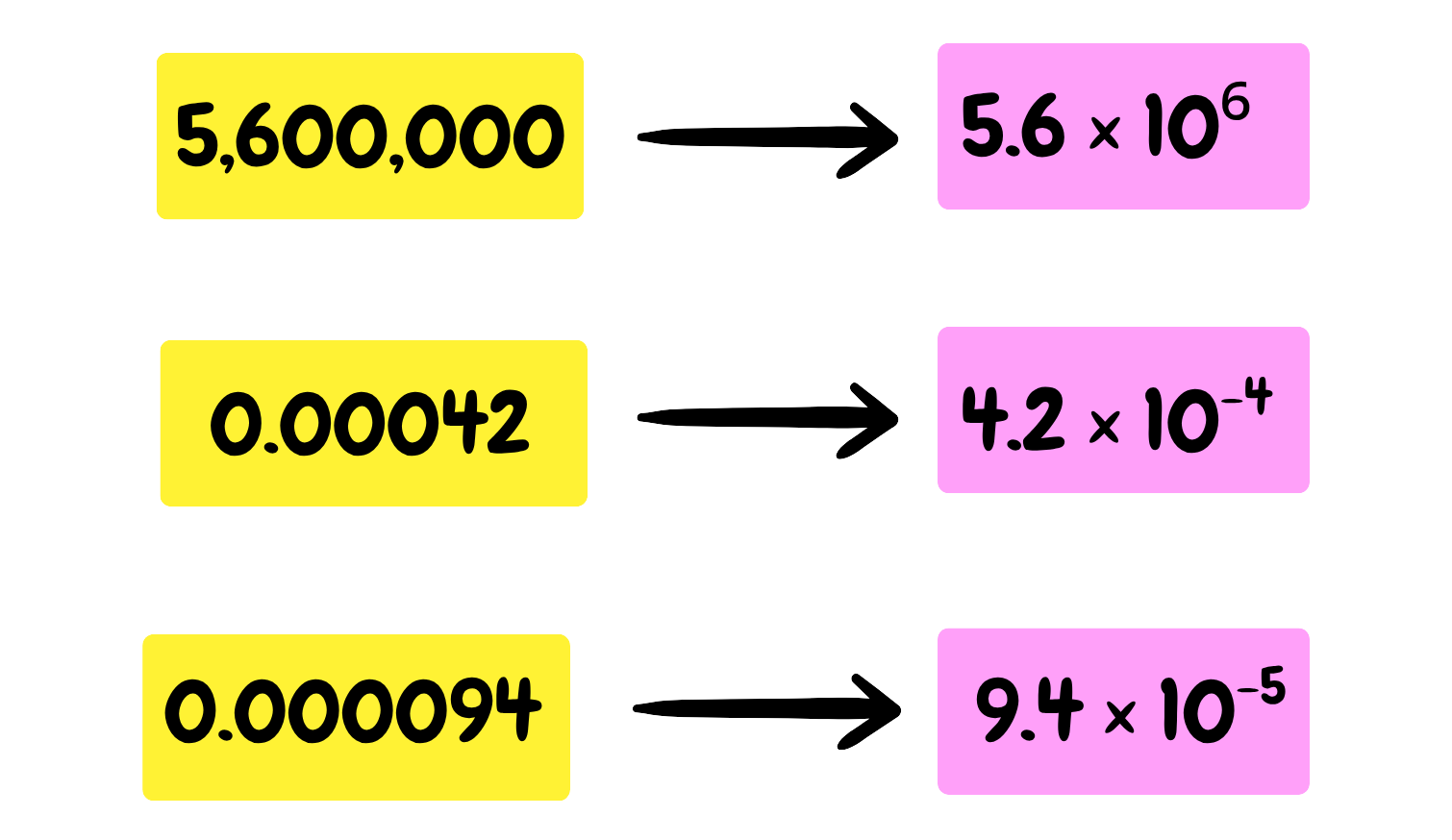
Examples: These are some of the conversions to their respective Standard Forms.
Why do we use Standard Form
- We use Standard Form because it makes numbers and equations easier to read, compare, and work with. Here’s a brief breakdown of why it’s useful:
1. Simplifies Large or Small Numbers – As we can simply write
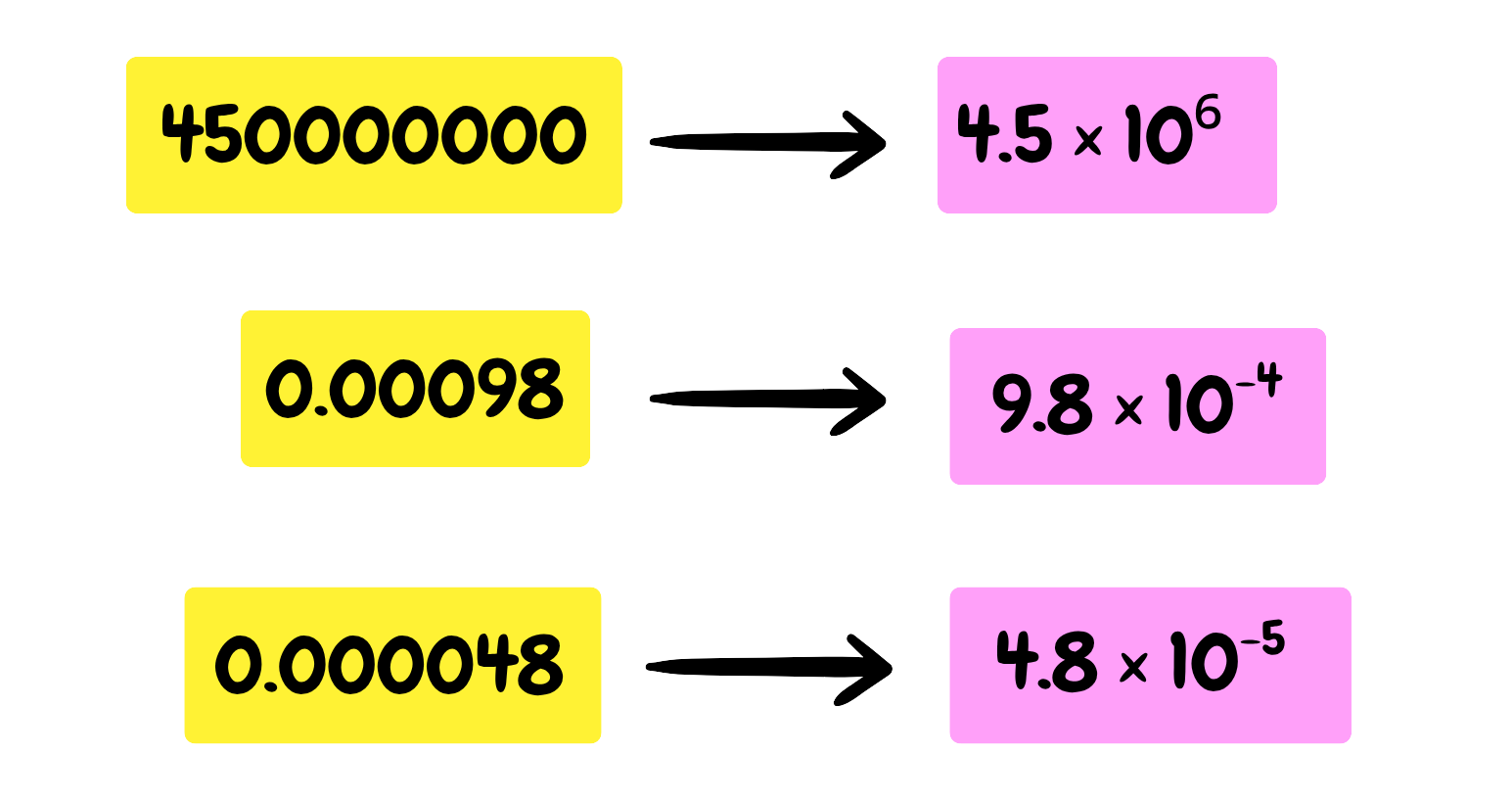
2. Comparision is Quicker – Numbers in standard form make it easier to compare magnitudes without counting zeroes.
- 4.5 x 1015 is far better and understandable than 4500000000000000
Converting into Standard Form
- There are mainly two types of numbers that can be converted in Standard Form.
Steps to convert a number to Standard Form:
1. Converting a Large Number
2. Converting a Small Number
 Solved Example:
Solved Example:
(Converting a Large Number)
Problem: Convert 640,000 to standard form.
Solution:
Step #1: Place the decimal after the first non-zero digit.
- The number is 640000, so place the decimal after 6.4
- This gives 6.4
Step #2: Count the number of places the decimal moved.
- The original decimal in 640000.0 moves 5 places to the left.
- So, the exponent is 5.
Step #3: Write the number in standard form:
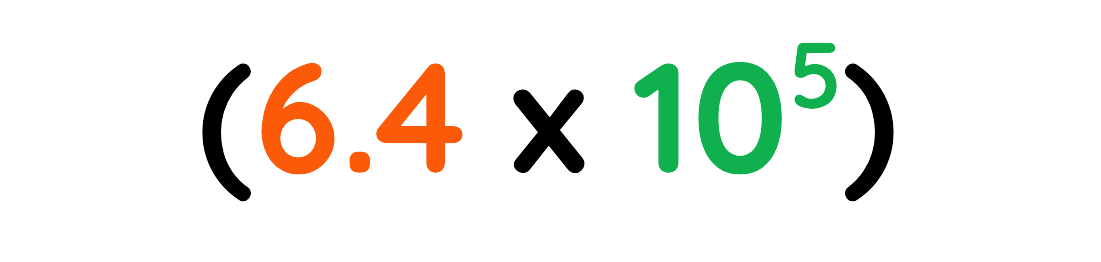
Final Answer: 6.4 x 105
 Solved Example:
Solved Example:
(Converting a Small Number)
Problem: Convert 0.0072 to standard form.
Solution:
Step #1: Place the decimal after the first non-zero digit.
- The number is 0.0072, so place the decimal after 7.2
Step #2: Count the number of places the decimal moved.
- The original decimal in 0.0072 moves 3 places to the right. So, the exponent is -3.
Step #3: Write the number in standard form:

Final Answer: 7.2 x 10-3
Addition in Standard Form
- Addition can be performed in Standard Form by this procedure:
Steps for Addition in Standard Form:
- Step #1: Make sure both of the numbers have the same power of 10.
- Step #2: Adjust one number accordingly so that both exponents match.
- Step #3: Add the coefficients while keeping the power of 10 the same.
- Step#4: Convert the result back into standard form (if necessary).
 Solved Example:
Solved Example:
(Adding Numbers with the Same Power of 10)
Problem: 4.3 × 103 + 3.9 × 103
Solution:
Step#1: Both numbers have 103, so just add the coefficients:

Step#2: Keep the same power of 10:
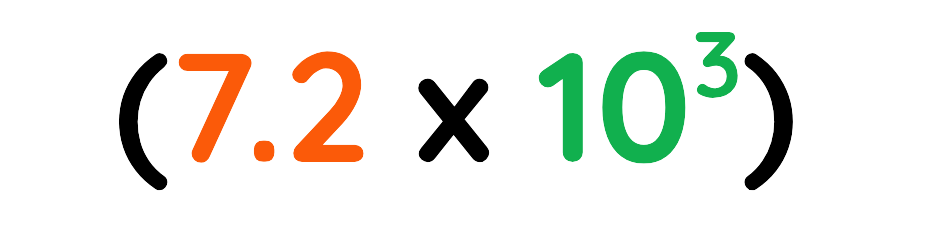
Final Answer: 7.2 x 103
 Solved Example:
Solved Example:
(Adding Numbers with Different Powers of 10)
Problem: 4.2 × 105 + 5.1 × 103
Solution:
Step#1: Convert both numbers to the same power of 10.

can be written as

Step#2: Now add the coefficients:

Step#3: Keep the power of 10:

Final Answer: 4.251 x 103
Subtraction in Standard Form
- Subtraction can also be performed in Standard Form by the given procedure:
Steps for Subtraction in Standard Form:
- Step #1: Make sure both of the numbers have the same power of 10.
- Step #2: Adjust one number accordingly so that both exponents match.
- Step #3: Subtract the coefficients while keeping the power of 10 the same.
- Step #4: Convert the result back into standard form (if necessary).
 Solved Example:
Solved Example:
(Subtracting Numbers with the Same Power of 10)
Problem: (6.8 × 103) – (2.5 × 103)
Solution:
Step#1: Both numbers have 103, so just subtract the coefficients:
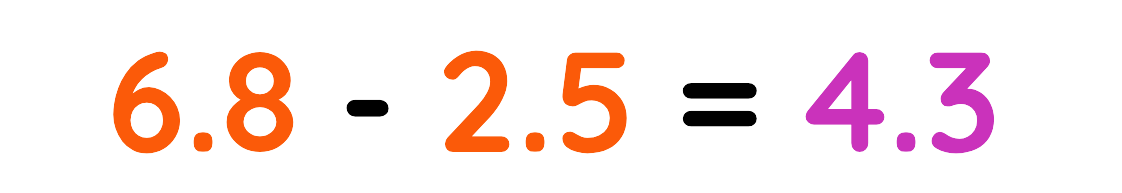
Step#2: Keep the same power of 10:

Final Answer: 4.3 x 103
 Solved Example:
Solved Example:
(Subtracting Numbers with Different Powers of 10)
Problem: (7.5 × 106) – ( 3.2 × 104)
Solution:
Step#1: Convert both numbers to the same power of 10.
- 3.2 × 104 can be written as 0.032 × 106
Step#2: Now subtract the coefficients:

Step#3: Keep the same power of 10:

Final Answer: 7.468 x 106
Multiplication in Standard Form
Multiplication can also be performed in Standard Form by the given procedure:
- Case 1: Multiplication with adjustments
- Case 2: Multiplication when the coefficient is greater than 10
 Solved Example:
Solved Example:
Problem: (4.5 × 105 ) × (2.0 × 102)
Solution:
Step#1: Multiply the coefficients:

Step#2: Add the exponents:
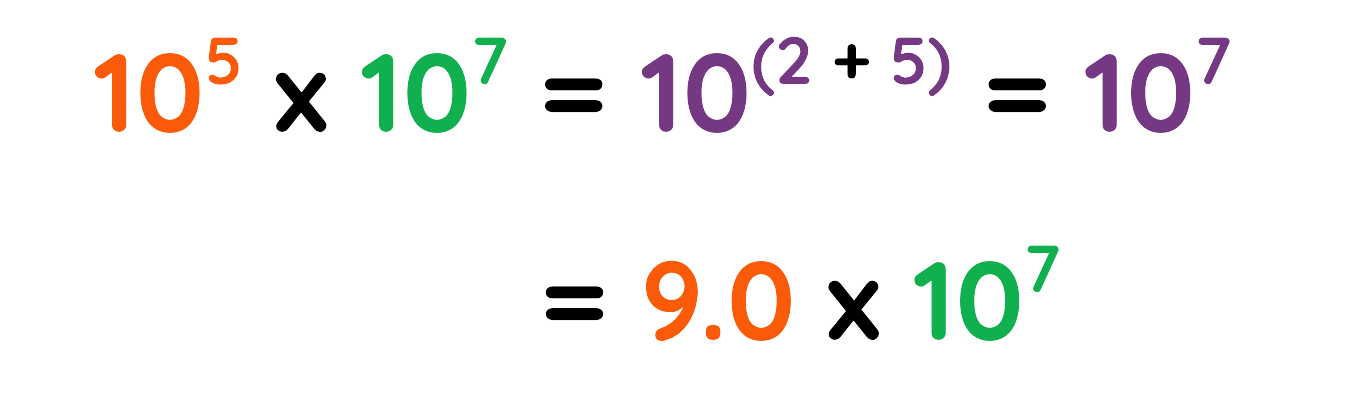
Final Answer: 9.0 x 107
 Solved Example:
Solved Example:
Problem: (6.2 × 103) × (5.0 × 102)
Solution:
Step#1: Multiply the coefficients:

Step#2: Add the exponents:

Step#3: The coefficient is greater than 10, so adjust:

Final Answer: 3.1 x 106
Division in Standard Form
Division can also be performed in Standard Form by the given procedure:
- Case 1: Simple Division
- Case 2: When the Coefficient is Less than 1
 Solved Example:
Solved Example:
Problem: (6 × 108) ÷ (2 × 106)
Solution:
Step#1: Divide the coefficients:

Step#2: Subtract the exponents:

Step#3: It comes out to be

Final Answer: 3 x 104
 Solved Example:
Solved Example:
Problem: (4.5 × 103) ÷ (9.0 × 105)
Solution:
Step#1: Divide the coefficients:

Step#2: Subtract the exponents:

Step#3: It comes out to be

Final Answer: 5 x 10-3
 Solved Example:
Solved Example:
Problem: Convert 567,000,000 to standard form.
(Standard Form GCSE Question)
Solution:
Step#1: Place the decimal after the first non-zero digit:
- 5.67
Step#2: Count how many places the decimal moves: 8 places to the left
Step#3: Write in standard form:

Final Answer: 5.67 x 108
 Solved Example:
Solved Example:
Problem: Convert 0.000042 to standard form.
(Standard Form GCSE Question)
Solution:
Step#1: Place the decimal after the first non-zero digit:
- 4.2
Step#2: Count how many places the decimal moves: 5 places to the right
Step#3: Write in standard form:

Final Answer: 4.2 x 105
 Solved Example:
Solved Example:
Problem: (3.2 × 104) + (4.5 × 103)
(Standard Form GCSE Question)
Solution:
Step#1: Convert 4.5 × 103 to match the power of 104

Step#2: Add the coefficients:
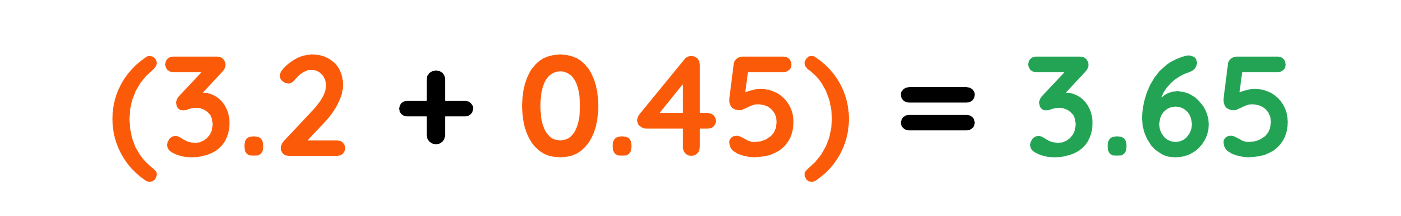
Step#3: Keep the power of 104

Final Answer: 3.65 x 104

