Waves: An Exploration of Types, Calculations, Speed and Differences

Practice Questions
Downloads

Introduction

  • Waves are fundamental to our understanding of Energy Transfer.
  • Waves are nature’s way of moving energy without moving matter.

Real life Example:

Illustration comparing sound waves entering an ear and light waves from a red beacon

Medical ultrasound imaging system and microwave oven representing types of waves

What are Waves?

  • Waves are a means of transferring energy from one place to another without the actual transfer of matter.
  • It is a fundamental concept in physics that applies to various types of waves, such as light wave and sound wave.
  • There is a transfer of energy from a source to your senses.

Diagram showing sound waves moving from a person speaking to another person’s ear

Types of Waves:

  • There are mainly two big categories of waves:

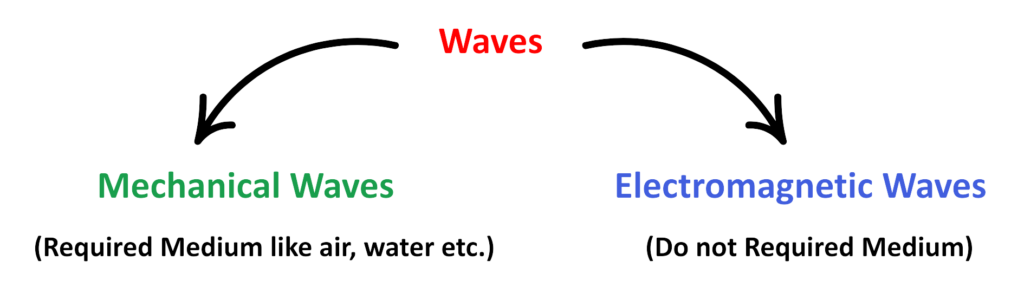
Diagram showing two main types of waves: Mechanical Waves and Electromagnetic Waves

Mechanical Waves: (Required Medium like air, water etc.)

  • Transverse Waves
  • Longitudinal Waves

Electromagnetic Waves: (Do not Required Medium)

  • Radio Waves
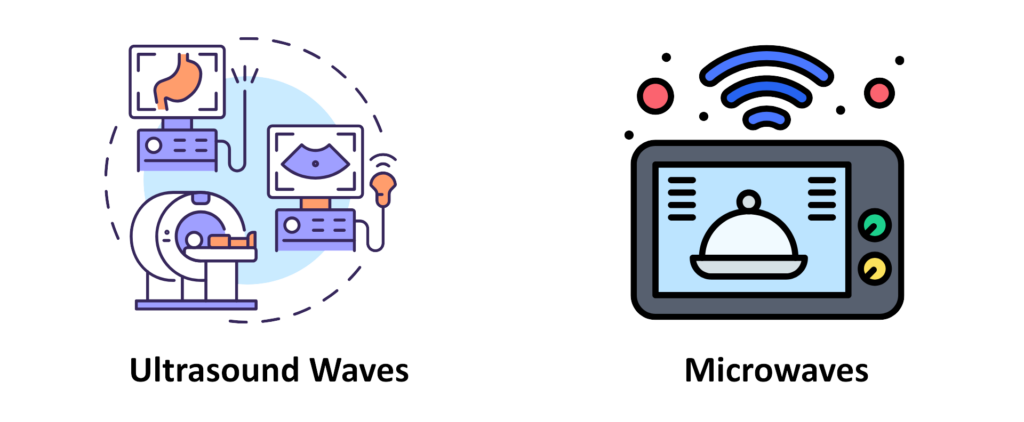
  • Microwaves
  • Infrared Waves
  • Ultraviolet (UV) Rays
  • X-Rays

What are the Components and Properties of Waves?

  • To understand wave better, it’s essential to know their key components and properties.

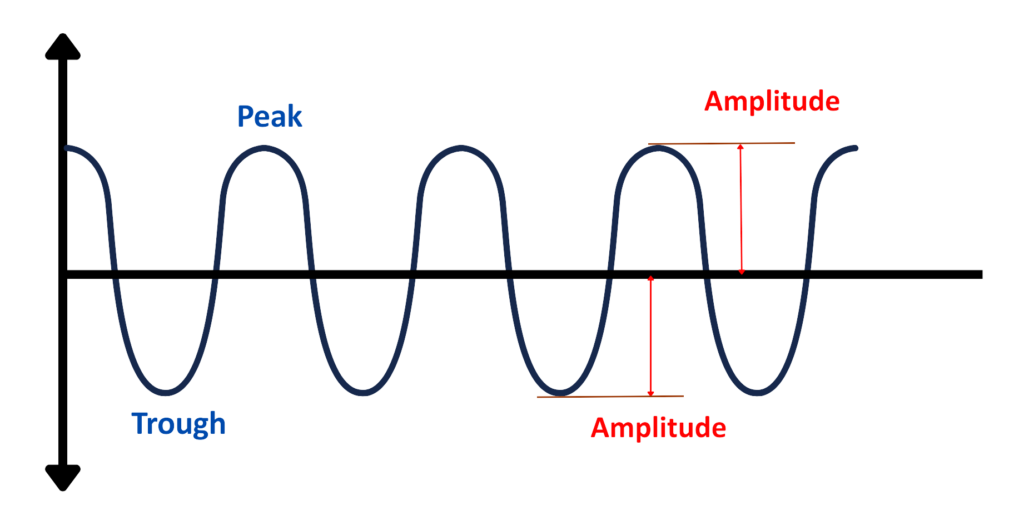
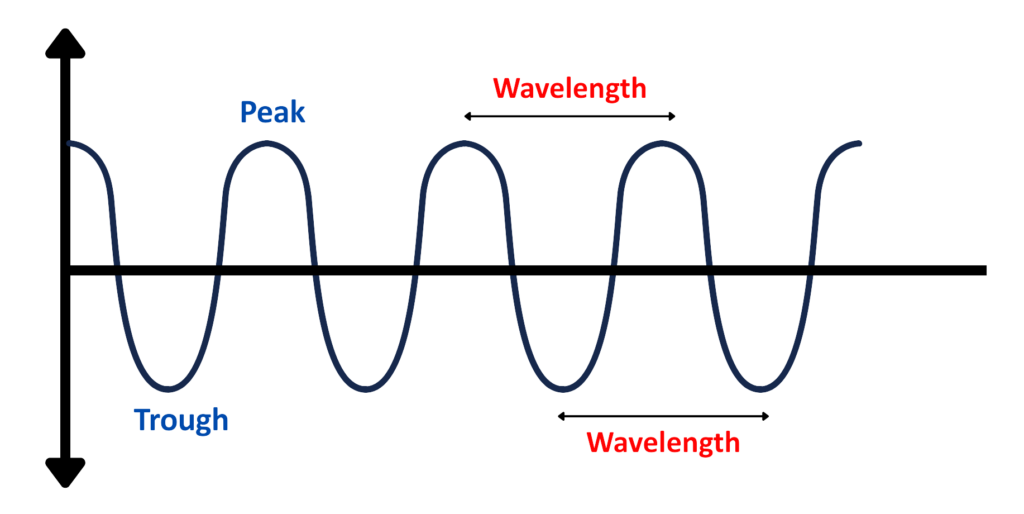
Amplitude:

  • The amplitude of a wave is the maximum displacement from the equilibrium position.
  • It’s the height of a wave from its resting point.

Wave diagram labeled with peak, trough, and amplitude

Frequency:

  • Frequency is the number of complete oscillations or cycles a wave completes per unit of time, typically measured in Hertz (Hz), which represents cycles per second.
  • A higher frequency means more oscillations in a given time period.
  • The frequency of a wave can be calculated using the equation:

Frequency equals one divided by time formula

Wave Speed:

  • Wave speed is a fundamental property that indicates how fast a wave travels.
  • It’s calculated by multiplying the wavelength by the frequency:

Wave speed equals wavelength times frequency formula

Where,

    • v = It is the wave speed in meters per second (m/s).
    • λ = It is the wavelength in meters (m).
    • f = It is the frequency in Hertz.

Wavelength:

  • Wavelength is the distance between two successive points in a wave that are in phase, typically measured from crest to crest or trough to trough.
  • It represents the length of one complete oscillation in the wave.

Diagram of a wave labeled with wavelength, peak, and trough

Time Period:

  • The Time Period of a wave is the time it takes to complete one full oscillation or one wavelength, measured in seconds.
  • It can be Calculated as,

Equation showing time period equals one divided by frequency

Distinguishing Between Transverse and Longitudinal Waves

  • Waves are classified into two main types:

Transverse waves:

  • In Transverse wave, the oscillations occur perpendicular (at right angles) to the direction of energy transfer.
  • Picture a wave travelling horizontally from left to right.
  • The particles involved in the wave move vertically, oscillating up and down.
  • One common example of a transverse wave is a light wave.

Real life Example:

Images showing examples of waves including ripples on water, guitar strings, light waves, and vibrating rope

Longitudinal Waves:

  • Longitudinal wave have oscillations parallel to the direction of energy transfer.
  • Imagine a slinky toy being stretched and compressed horizontally.
  • As the wave moves, the coils of the slinky move back and forth in the same direction as the wave itself.
  • A classic example of a longitudinal wave is a sound wave.
  • When you hear a sound, it’s the result of air particles compressing and expanding as the wave of energy passes through.

Real life Example:

Sound waves, seismic P waves, ultrasound waves, and spring vibrations representing longitudinal waves

How to Calculate Wave Speed?

  • Calculating Wave Speed is a fundamental concept in understanding how wave behave and interact with their surroundings.
  • It can be Calculated as:

Wave speed equals wavelength times frequency formula

Where,

    • Wave Speed (v) = This is what we want to find, measured in meters per second (m/s).
    • Wavelength (λ) = Measure the length of one complete oscillation, typically in meters (m).
    • Frequency (f) = Determine how many complete oscillations occur per second, measured in Hertz (Hz).

certified Physics and Maths tutorSolved Example

Problem: A sound wave has a frequency of 500 Hz and a wavelength of 0.68 m. Calculate its speed.

Solution: 

Step #1: Given:

    • Frequency (f) = 500 Hz
    • Wavelength (λ) = 0.68 m

Step #2: Applying the formula:

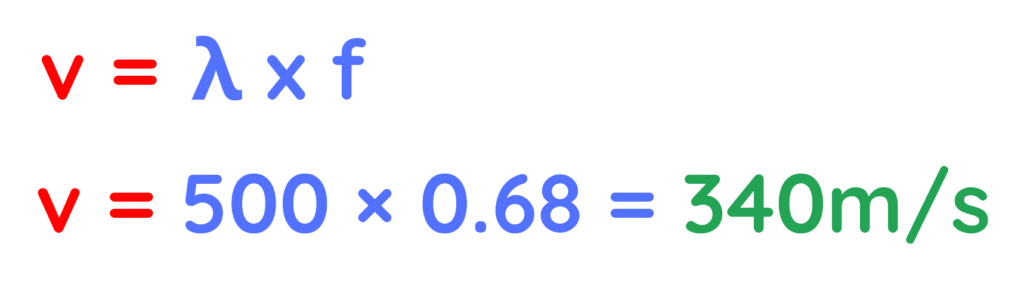
Equation showing wave speed equals wavelength times frequency with numerical example v = 500 × 0.68 = 340 m/s

The wave speed is 340 m/s

Final Answer: 340 m/s

certified Physics and Maths tutorSolved Example

Problem: A sound wave in water has a wavelength of 2.5 meters and travels at 1500 m/s. What is its frequency?

Solution: 

Step #1: Given:

    • Wave Speed (V) = 1500 m/s
    • Wavelength (λ) = 2.5 m

Step #2: Applying the formula:

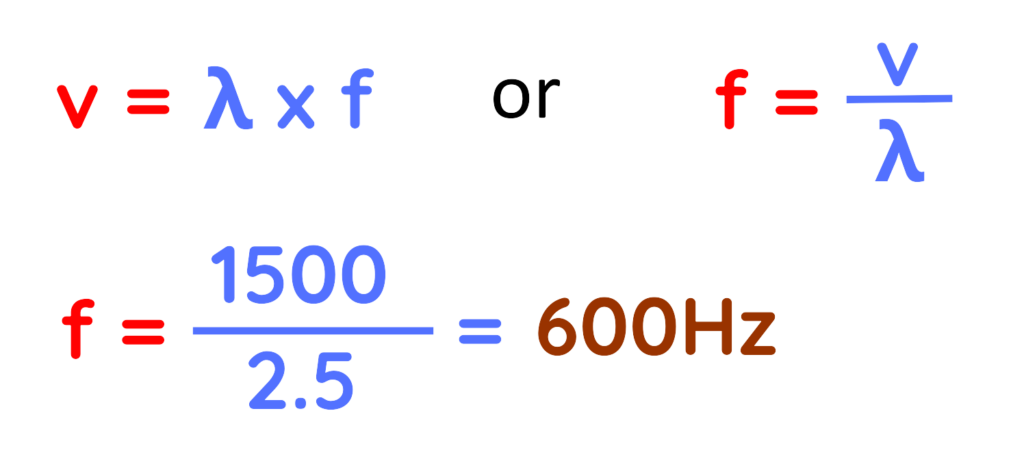
Formula showing frequency equals wave speed divided by wavelength with an example f = 1500 ÷ 2.5 = 600 Hz

The Frequency is 600 Hz.

Final Answer: 600 Hz

certified Physics and Maths tutorSolved Example

Problem: A radio station transmits at 105.3 MHz. If the speed of radio waves (a type of EM wave) is 3 × 108 m/s3, what is the wavelength?

Solution: 

Step #1: Given:

    • Frequency (f) = 105.3MHz = 105.3 × 106Hz
    • Wave Speed (v) = 3 × 108 m/s3

Step #2: Applying the formula:

Equation showing how to calculate wavelength from wave speed and frequency with example λ = 3×10⁸ ÷ 105.3×10⁶ = 2.85 m

The wavelength is 2.85 meters.

Final Answer: 2.85 meters

Request for Demo Lesson

Table of Content