Variable Acceleration: An Easy and Enjoyable Journey to Mastery
Today, we’re diving into an exciting topic in kinematics: Variable Acceleration
We’ve already covered the applications of SUVAT equations with constant acceleration.
If you haven’t watched that video, you can click on this link. SUVAT Equations


If you’re seeking a more personalized and tailored approach to mastering Variable Acceleration and tackling SUVAT Equations with confidence, look no further. My one-to-one tutoring is designed to cater to your unique learning style, pace, and academic goals. Together, we’ll conquer the challenges of variable acceleration and excel in A-level kinematics.
Whether you’re preparing for your GCSE or A-Level exams, you can click on this link: Physics Private Tutoring
Delve deeper into the world of SUVAT Equations by clicking on the link for an in-depth exploration and a comprehensive understanding: SUVAT Equations
If you want to watch a Video tutorial, please watch this video:
Contents
Chapter 1
Variable Acceleration
Now, let’s take things to the next level! Real-world scenarios often involve variable acceleration, where the velocity changes at different rates throughout motion due to factors like air resistance and friction.

But fear not, as we have a few formulas with differentiation and integration that can help us solve all questions related to variable acceleration.

Let’s start with the basic definition of acceleration. We know acceleration is the change in velocity divided by time taken.

The same formula, when written in the form of a derivative, will give us “a = dv/dt.” That means by differentiating the velocity function, we can obtain acceleration.
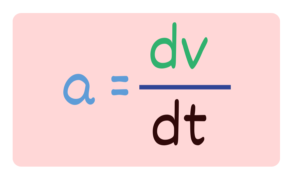
Also, if we multiply “dt” on both sides, we get the integral of “a times dt = dv” Therefore, by integrating acceleration with respect to time, we get the change in velocity.

Chapter 2
Velocity
Next, lets move to the basic definition of velocity.
Velocity is the change in displacement divided by time taken, or “v = ds/dt.”

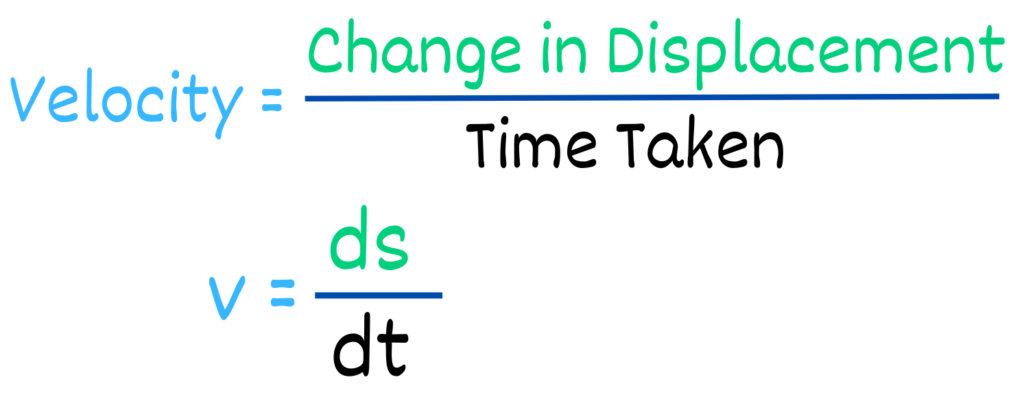
So, differentiating the displacement function gives us velocity. Similarly, if we multiply “dt” on both sides, we get the integral of velocity with time, which gives us the change in displacement or displacement itself.

Chapter 3
Conclusion
In conclusion, differentiating velocity gives us acceleration, while integrating velocity gives us displacement. And if we integrate acceleration, we get back velocity. Likewise, differentiating displacement will also give us back velocity.

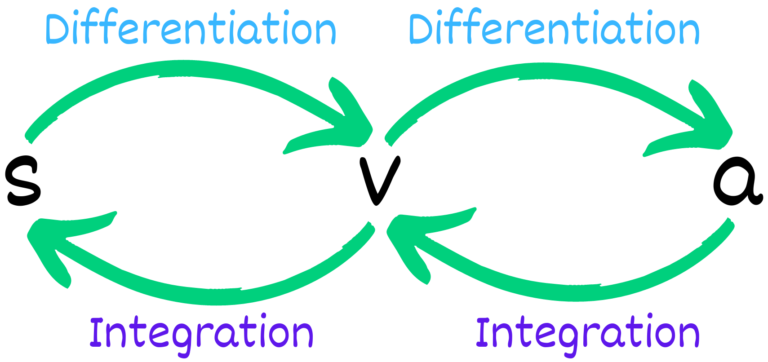
Now, we must know that we can only follow these formulas if we are given acceleration, velocity, and displacement as functions of time.

However, in some questions, we are given acceleration as a function of displacement.

In all such situations, we can use the formula: “integral of v dv = integral of a ds.”
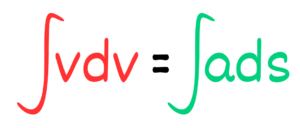

Chapter 4
Practice Questions
Now, lets Practice a few Questions:

Application 1: Free-Falling Object

Solved Example : We are given a free-falling object with variable acceleration. The object starts from rest and its velocity changes with time according to the equation v = 9.8t – 4.9t2.
Our task is to find the displacement of the object after 3 seconds.
Solution: The object
starts from rest, and its velocity changes with time according to the equation
v = 9.8t – 4.9t2. We need to find the displacement of the object
after 3 seconds.
Step 1: Integration of Velocity Equation
To find the displacement (s), we need to integrate the velocity equation with respect to time (t).
The velocity equation is v = 9.8t – 4.9t2
The integral of v dt will yield the displacement function s(t).
Step 2: Integrating the Equation
Integrate the equation v = 9.8t – 4.9t2 with respect to time (t).
The result will be the displacement function s(t) in terms of t and the constant of integration, C.
Step 3: Finding the Constant of Integration
After integrating, we get
s = 9.8t2/2 – 4.9t3/3 + C,
where C is the constant of integration.
Step 4: Calculating Displacement at t = 3 seconds
- Plug in the initial limit of time (0 seconds) and the final limit (3 seconds) into the displacement function s(t).
- Evaluate s at t = 3 seconds to find the displacement of the object at that time.
Step 5: Solving for the Displacement
Evaluate the expression
s = (4.9(3)2 – 4.9(3)3/3 + C) – (4.9(0)2 – 4.9(0)3/3 + C).
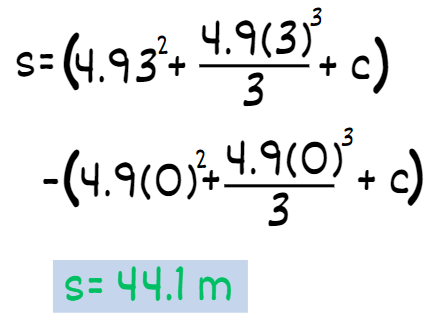
Answers: we get s = 44.1 meters as the displacement of the object after 3 seconds.
Accelerating Car with Variable Acceleration

Solved Example: Suppose a car starts from rest and accelerates with an acceleration given by a = 2t, where a is the acceleration in m/s2 and t is the time in seconds.
Find the distance traveled by the car after 5 seconds.
Solution
Step 1 & 2 : Sketch a Diagram & Identify Knowns and Unknowns
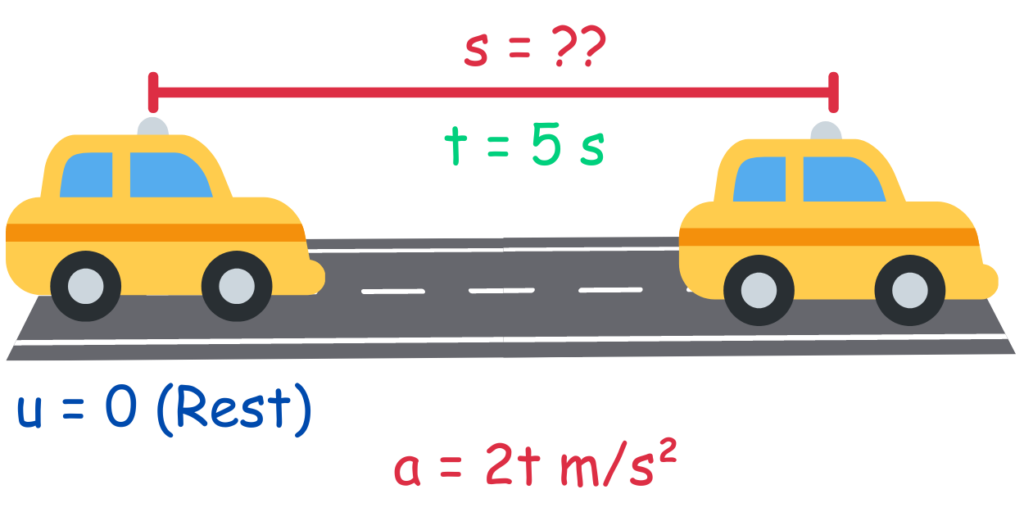
Step 3: Select the Appropriate Equation(s)
We need an equation that relates the knowns (t, a) to the unknown (s). In this case, we can use the equations:
dv = ∫ a dt
ds = ∫ v dt
Step 4: Solve the Equation(s)
Plug in the known values into the equation:
dv = ∫ (2t) dt
Integrating the equation, we get:
v = t2 + C
Now since the initial velocity is Zero, so at t = 0, v = 0
0 = 02 + C
we get C = 0
v = t2
ds = ∫ v dt
ds = ∫ t2 dt
s = t3 / 3 + C
Again here, since the initial velocity is Zero, so at t = 0, s = 0
0 = 03 + C
again, we get C = 0
These formulas, involving differentiation and integration, provide the necessary mathematical tools to handle variable acceleration problems and analyze the complex motion of objects experiencing changing velocities due to external forces and factors.
Let’s try to use these formulas in the coming chapters.
But if you want a calculator to simply answer all your questions you can simply use this link: Kinematics Questions Calculator




