Surds: Questions, Steps, Examples & Worksheet

Surds

Surds are an important part of mathematics that many students find challenging.
Surds play a crucial role in expressing exact values, particularly in geometry and algebra.
They provide a means to represent square roots without relying on decimal approximations, allowing for more accurate mathematical calculations.

In this article, we will discuss:

What is a Surd?
Explore Surds – Addition, Subtraction, Multiplying, Division and Rationalisation.

Here is one more link to practice a few extra questions: Maths Genie Surds Questions

What is a Surd?

A surd is a square root or any root that cannot be simplified to a rational number.
Surds are represented by the symbol √ and are commonly found in mathematics and physics.
The most basic example of a surd is the square root of 2 (√2), which cannot be expressed as a fraction of two integers.

Surds - Addition and Subtraction

Adding and subtracting surds can be tricky, but there is a simple rule to follow.
To add or subtract surds, the terms inside the roots must be the same.
For example, we can add 2√2 and 5√2, but not 3√2 and 2√5.

Let’s consider the following example:

To simplify this expression, we first add and subtract the terms with the same root, giving:

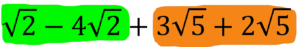
Simplifying further, we get:

Multiplying Surds

Multiplying surds involves multiplying the terms outside the roots and the terms inside the roots separately.
For example, to multiply √2 by √3, we multiply 2 by 3 to get 6 and then take the square root of 6.

Also, the part with Surd is multiplied with Surd and the integer part is multiplied with the integer part:
For example:

Let’s consider the following example:

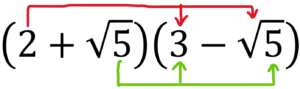
To simplify this expression, we use the distributive property of multiplication, giving:

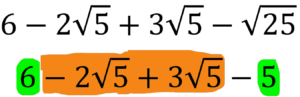
Simplifying further, we get:

Surds Division

Dividing surds is similar to multiplying them, but we need to take the reciprocal of the divisor and then multiply.
For example, to divide √2 by √3, we first take the reciprocal of √3, which is 1/√3. Then, we multiply √2 by 1/√3 to get (√2 / √3) = √6/3.

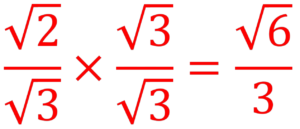
Surds Rationalisation (Simpler)

Sometimes, we need to simplify an expression that contains a surd in the denominator. This process is called surd rationalisation.
The simpler method involves multiplying the numerator and denominator by the surd in the denominator.
For example, to rationalise 4/√3, we multiply the numerator and denominator by √3, which gives:

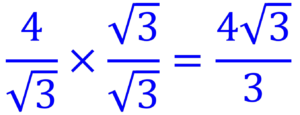
Surds Rationalisation (Higher)

The higher method of surd rationalisation involves multiplying the numerator and denominator by the conjugate of the surd in the denominator.
The conjugate is the surd with the opposite sign between the two terms. For example, to rationalise 1/(√3 + √2), we multiply the numerator and denominator by (√3 – √2), which gives:

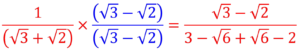
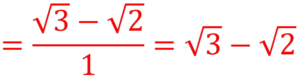
Solved Example:

Question 1: Rationalise the denominator of the fraction: (5√2) / (2 – √2)

Solution:

Step #1: Multiplying the numerator and denominator by the conjugate of the denominator,

we get:

[(5√2) / (2 – √2)] × [(2 + √2) / (2 + √2)]

Step #2: Simplifying the expression, we get:

[(5√2) (2 + √2)] / [(2 – √2) (2 + √2)]

[10√2 + 5 × 2] / (2² – √2²)

(10√2 + 10) / 2

5√2 + 5

Question 2: Rationalise the denominator of the fraction: (1 + √3) / (2 – √3)

Solution:

Step #1: Multiplying the numerator and denominator by the conjugate of the denominator,

we get:

[(1 + √3) / (2 – √3)] × [(2 + √3) / (2 + √3)]

Step #2: Simplifying the expression, we get:

[(1 + √3) (2 + √3)] / [(2 – √3) (2 + √3)]

(2 + √3 + √3 + √9) / (2² – √3²)

(2 + 2√3) / 1

2 + 2√3

Practice Questions

Question 1: Rationalize the denominator: (2 / (√5 + √3)).

Answer :

Question 2: Rationalize the denominator: (3/(√10 + √2)).

Answer :

Worksheet on Surds

Question 1: Simplify √12

Question 2: Rationalize the denominator: (2/√3)

Question 3: Rationalize the denominator: (3/√2).

Question 4: Rationalize the denominator: (1/(√7 + √3))..