Similarity – GCSE Maths

Practice Questions
Downloads

Introduction

  • Similarity of shapes means that the shapes are same but they have different size, with equal corresponding angles and proportional sides.
  • Concept of Similarity is applied in many places like linear algebra and data analysis to measure how much the two objects or datasets are similar.

Similarity: Multiple shapes and triangles showing similarity through same angles and proportional sides

  • Concept of Similarity – In Geometry –
  • To determine properties of shapes and solve problems that involve proportions.
  • In Computer Science – To detect patterns and compare objects.

Similar Shapes

  • Similar Shapes are those which are of same shape but have different size. The key characteristics of Similar Shapes are –
  • Same corresponding Angles
  • Same Shape Different size (proportional sides)

Similarity: Two similar quadrilaterals with matching angles and proportional sides labeled 1cm:2cm and 3cm:6cm

SCALE FACTOR:

  • The Scale Factor tells us how much bigger the larger shape is than the smaller one.

Similarity: Scale factor formula showing side length of larger shape divided by side length of smaller shape

  • As the scale factor from smaller to larger shape is positive (greater than 1) we prefer using it to solve questions rather than from larger shape to smaller (lesser than 1 and create complexity).
  • The following rectangles are similar because they are of same shape and the equal corresponding angles with proportional sides.

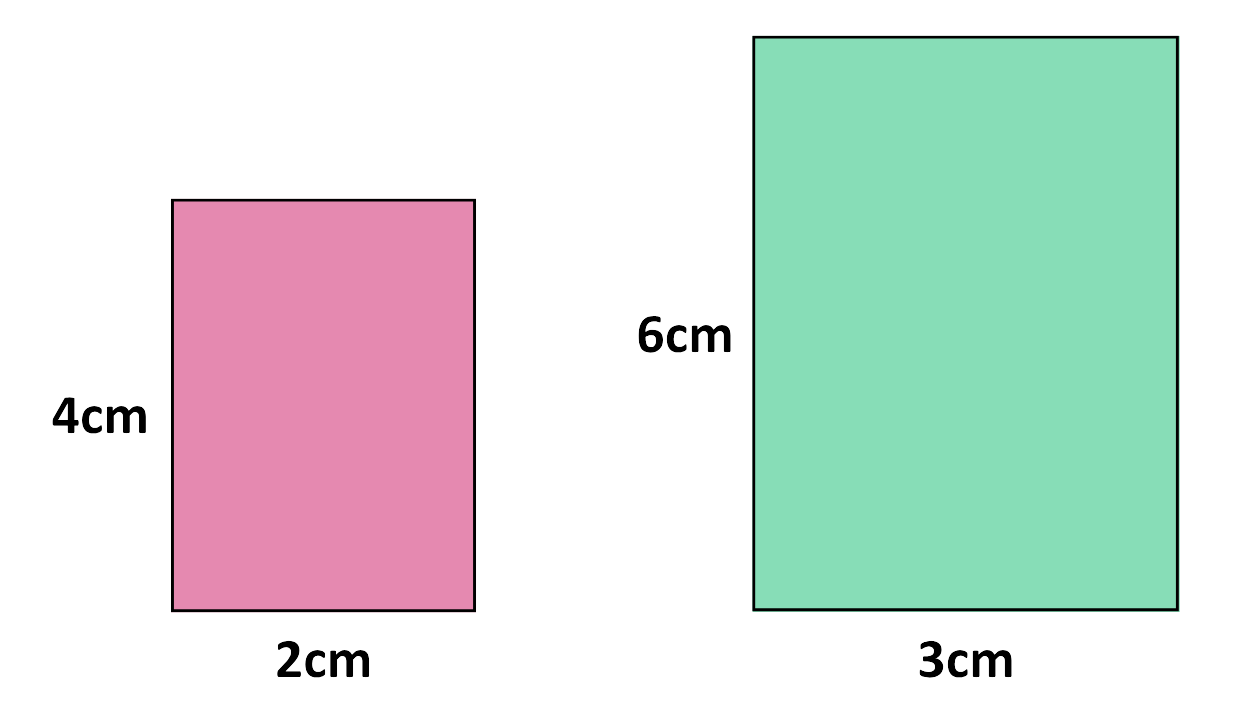
Similarity: Two similar rectangles with dimensions 2cm by 4cm and 3cm by 6cm

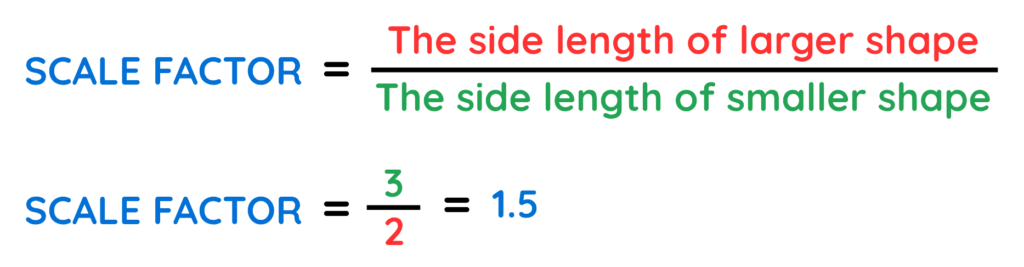
Similarity: Formula for scale factor with an example showing 3 divided by 2 equals 1.5

  • It is same for the other sides also-

Similarity: Scale factor calculation example showing 6 divided by 4 equals 1.5

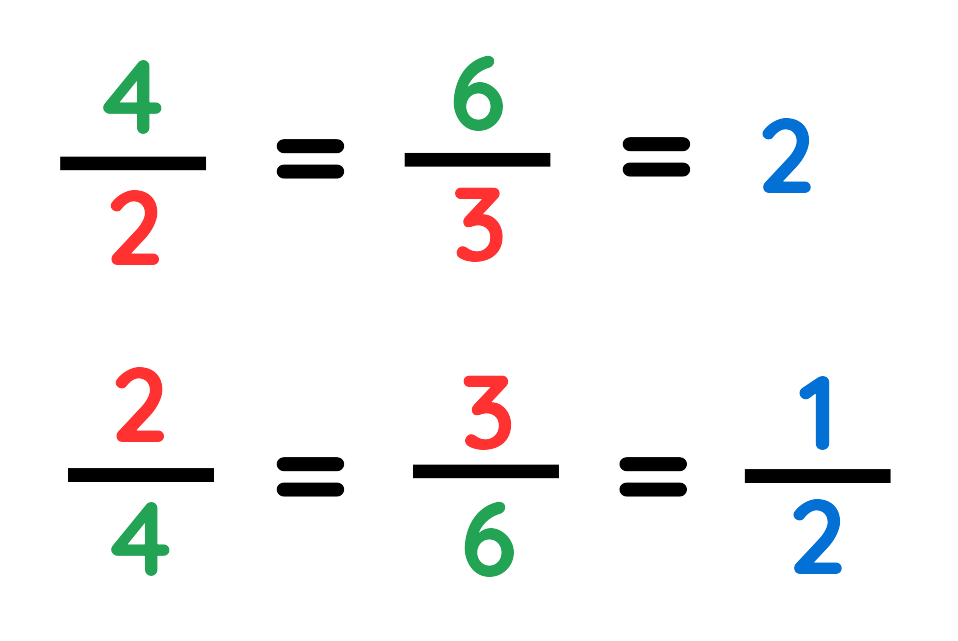
  • The ratio of the corresponding sides is also same in both the shapes –

Similarity: Comparing fractions to find scale factors with examples like 4 over 2 equals 6 over 3 equals 2

certified Physics and Maths tutorSolved Example

Problem: If the following pair of shapes are similar then find out the missing Sides/Angles?

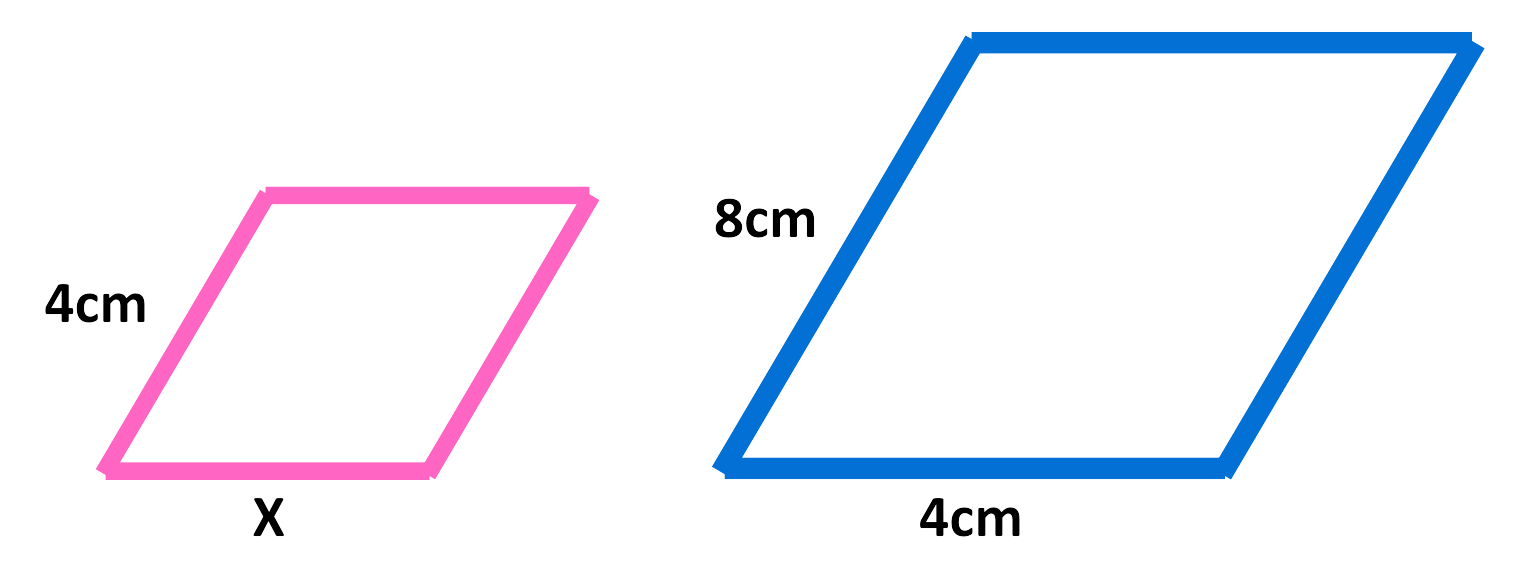
Solution: 

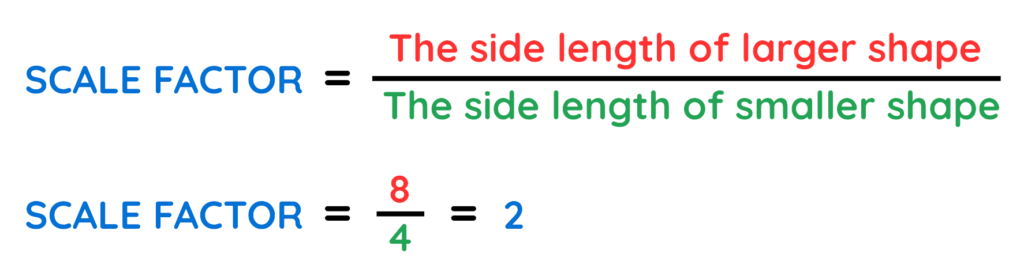
We know that –

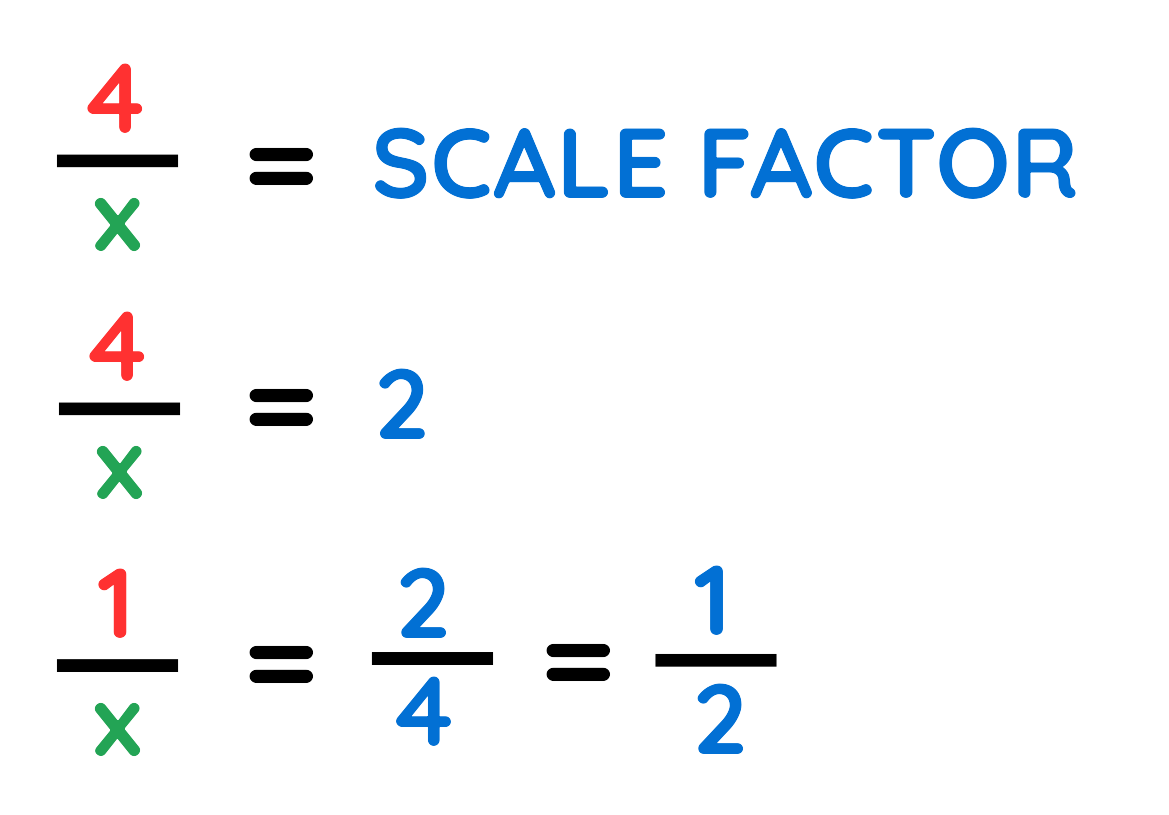
Final Answer: x = 2 cm

certified Physics and Maths tutorSolved Example

Problem: Find the value of Angle Y and side X?

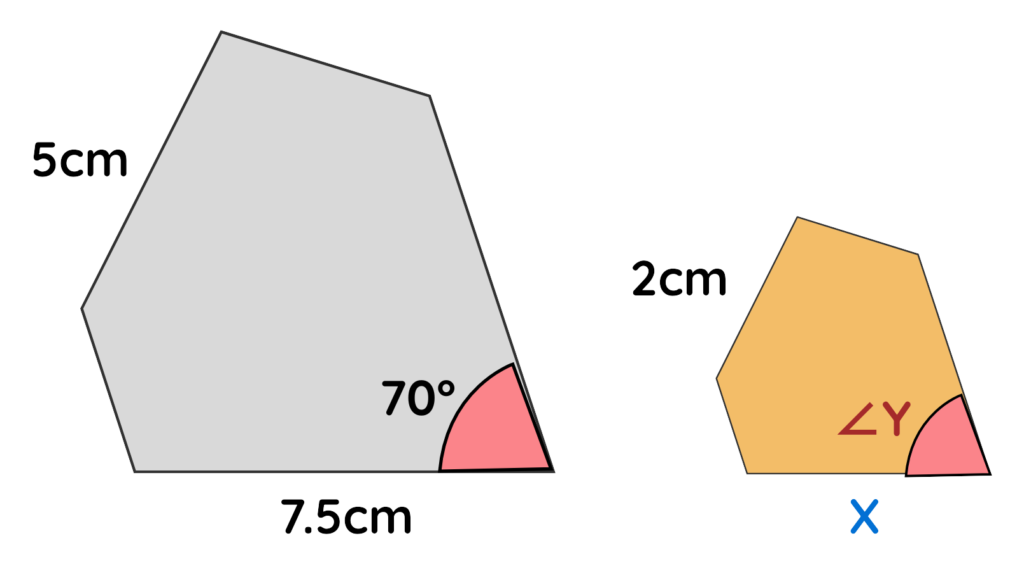
Similarity Solved Example Questions 1

Solution: 

We know that in similar shapes, the corresponding angles are always equal so –

∠Y = 70°

Also-

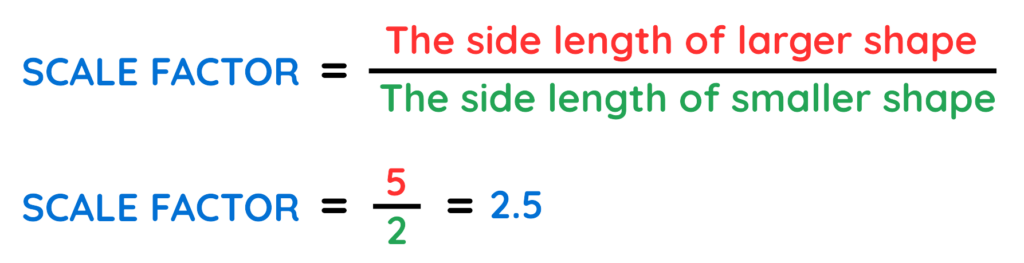
Similarity Solved Example Questions 1 Part 1

We Know that –

Similarity Solved Example Questions 1 Part 2

Final Answer: x = 3 cm and ∠Y = 70°

certified Physics and Maths tutorSolved Example

Problem: Show that the polygon ABCDE is similar to PQRST?

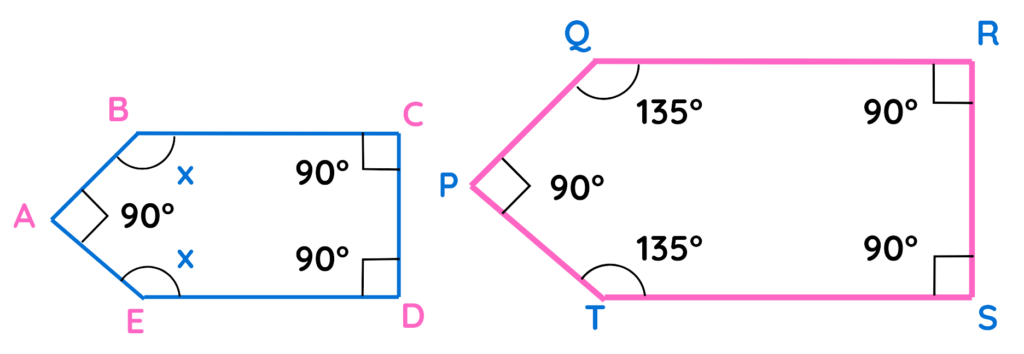
Similarity Solved Example Questions 2

Solution: 

The shape of polygon ABCDE is same as that of PQRST, but we need to check the corresponding angles are equal or not. For this we calculate the missing angles of the polygon ABCDE –

As The polygon is a pentagon the sum its angle is 540°. Thus,

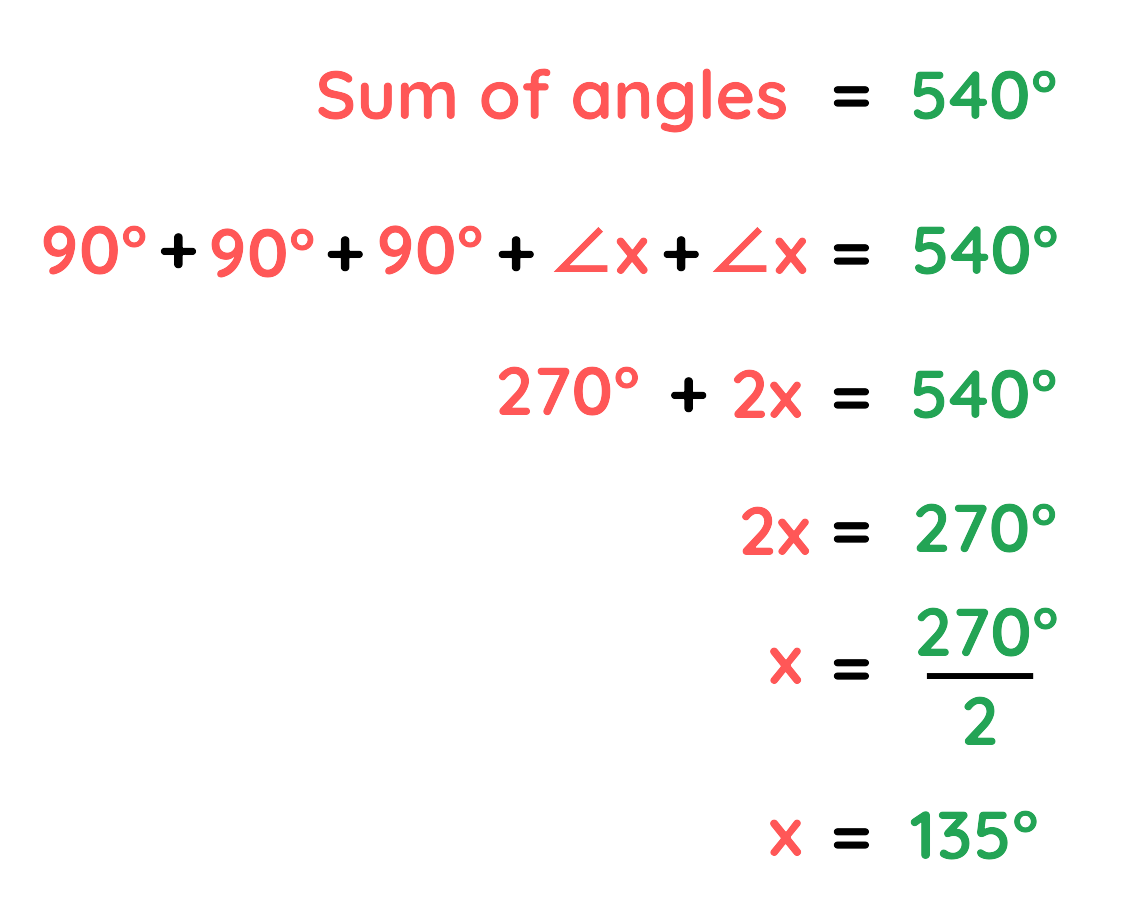
Similarity Solved Example Questions 2 Part 1

As all the corresponding angles of the two polygons came out to be equal we can conclude that they are similar.

Final Answer: x = 135°

Similar Triangles

  • Similar Triangles are those which are of the same shape but different size along with equal corresponding angles and proportional sides.
  • The Length scale factor formula is same in case of triangles as that of the other shapes.

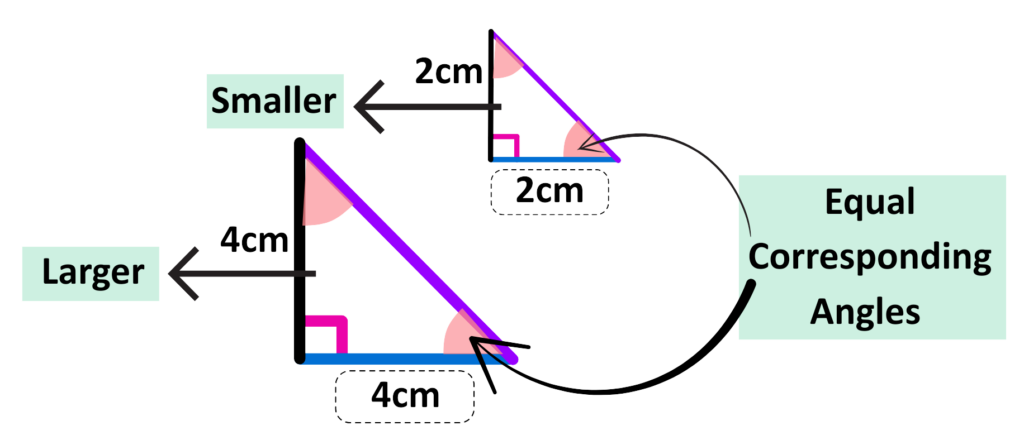
Two right-angled triangles with equal corresponding angles and proportional side lengths

Scale factor formula showing side length of larger shape divided by side length of smaller shape

certified Physics and Maths tutorSolved Example

Problem: Are the following triangles similar if yes find length scale factor?

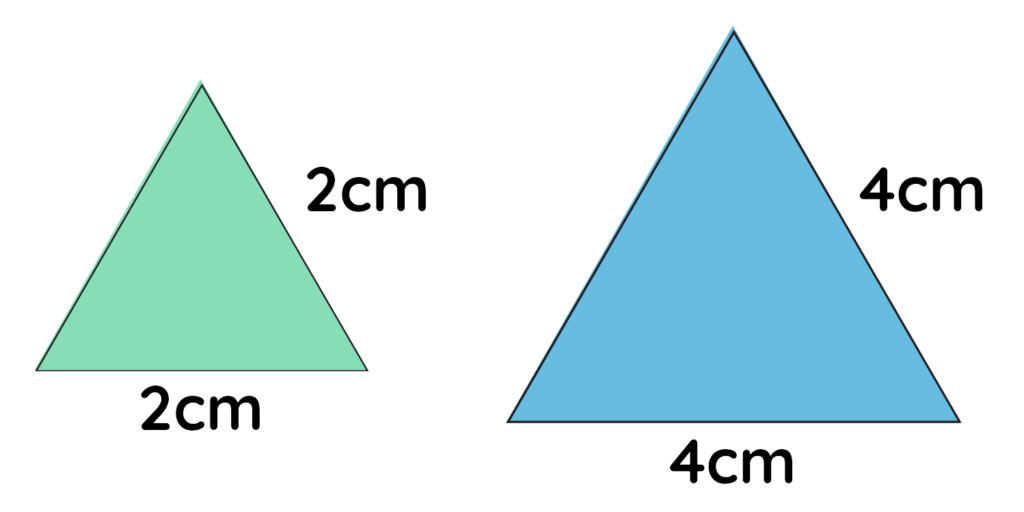
Solution: 

Yes, because the shape is same and sides are in proportion –

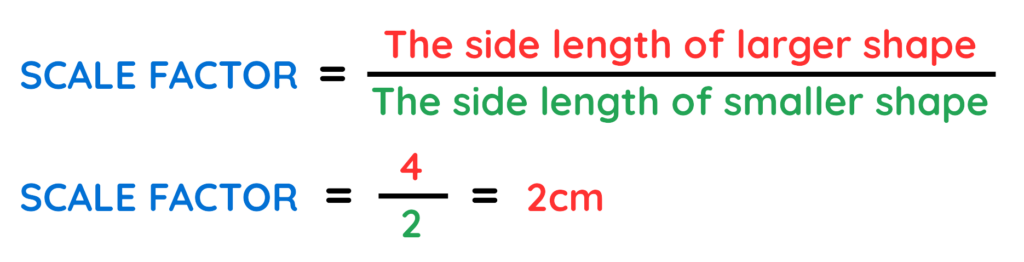
Final Answer: 2 cm

certified Physics and Maths tutorSolved Example

Problem: Are the following triangles similar? Give reason.

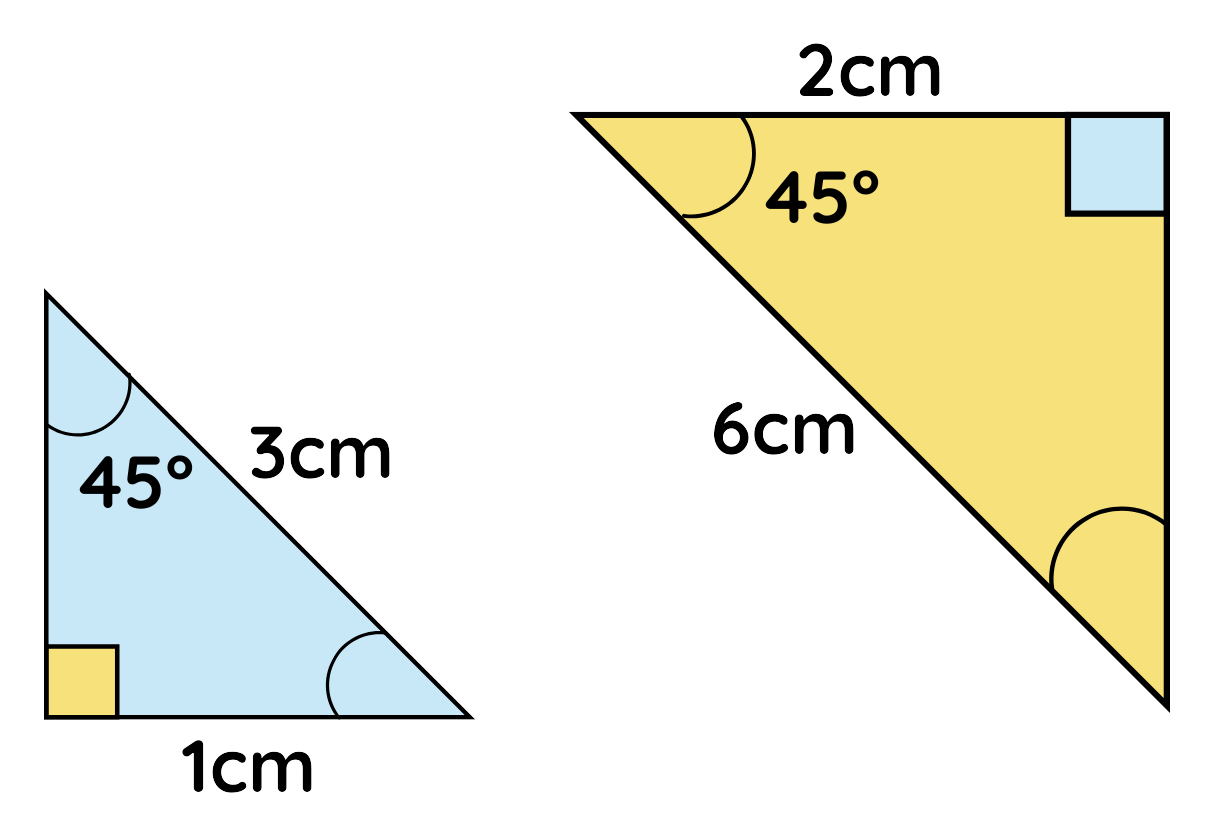
Solution: 

Yes, the triangles are similar as the corresponding angle equal and the shape is equal also the sides are in proportion –

Final Answer: 2 cm

certified Physics and Maths tutorSolved Example

Problem: Find out the missing sides of the triangle shown in diagram –

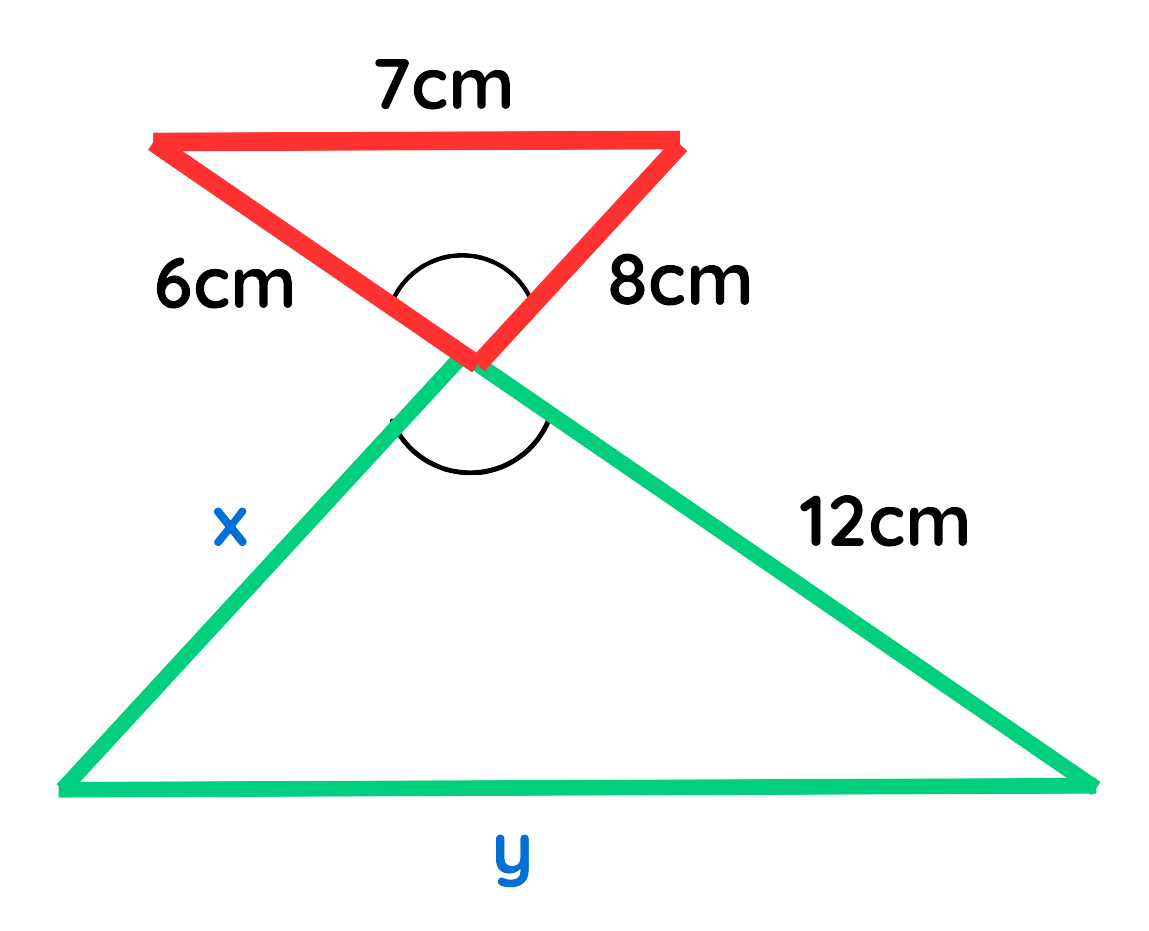
Solution: 

The Triangles shown in above diagram are similar, because –

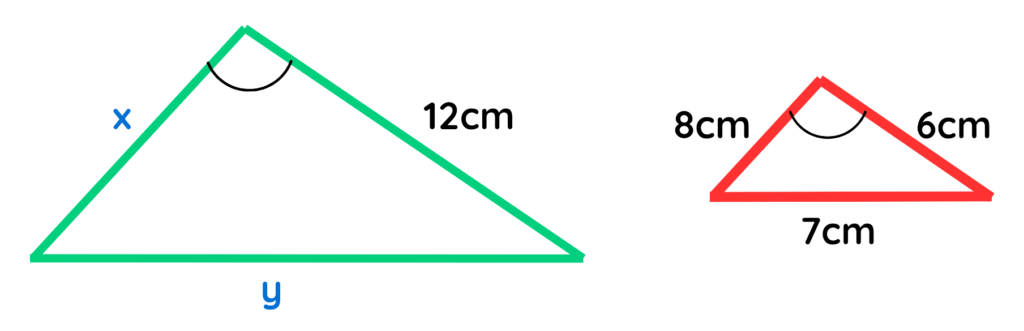
According to the interior angle property of parallel lines –

a = e

b = f

Vertically Opposite Angles –

c = d

image

Since the triangles are similar their sides should be in proportion means that –

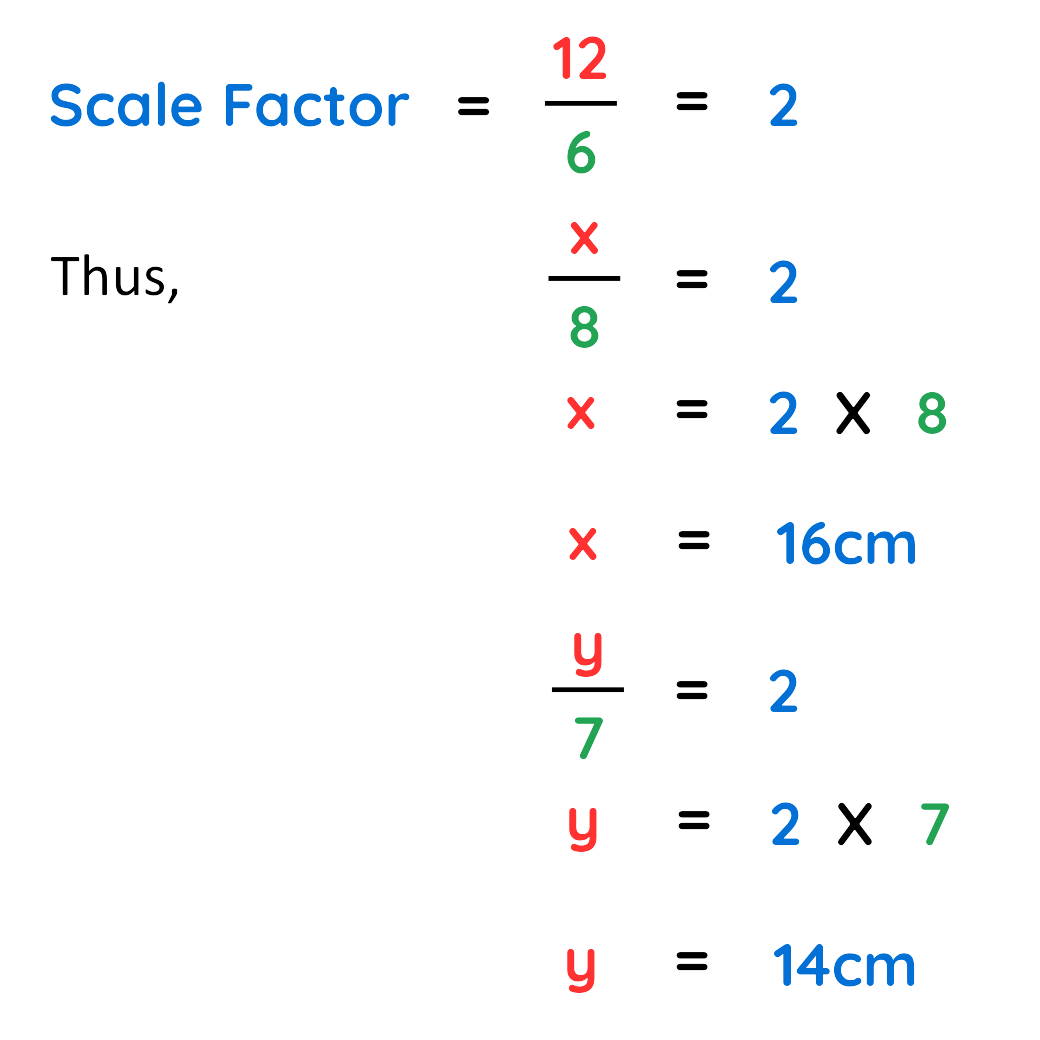
Final Answer: x = 16 cm and y = 14 cm

Table of Content

Join Tutoring