Similar Shapes: Step-by-Step Examples with Worksheet

Calculator
Test Yourself

Similar Shapes

  • The similar shapes are the core component of geometry which reveals the proportional relationship between the measures of corresponding angles and sides.
  • Fundamental to geometry is the recognition of shapes in different fields, like architecture and engineering, that shape comparison and scaling depend on.

In this article, we will discuss: 

  1. What are similar shapes?
  2. Working with Similar Shapes Involving Area or Volume

Here is one more link to practice a few extra questions: Maths Genie Similar Shapes Questions

What are similar shapes?

The similar shapes in mathematics are those in which the first one is a proportional enlargement of the other.

Scale Factors:

When two shapes are similar and connected by a scale factor, denoted as ‘k’:

    • In equivalent areas, areas are connected with an area factor ‘k2‘.
    • Equivalent volumes are characterized by the volume factor k3.

Working with Similar Shapes Involving Area or Volume

Step #1 – Identification:

  • Identify the known quantities which are units of lengths, areas or volumes.

Step #2 – Direction:

  • Find out whether the shapes are getting larger or smaller.

Step #3 – Scale Factor Calculation:

  • Identify the Scale Factor (‘k’) by two given lengths, areas or volumes.

  • Look whether the scale factor is greater than one for expansion or less than one for contraction.

  • Express the scale factor as ‘k = s.f.’ for lengths, ‘k2 = s.f.‘ for areas, and ‘k3 = s.f.‘ for volumes.

Step #4 – Utilizing Scale Factor:

  • Use the known scale factor for magnifying other relevant lengths, areas, or volumes.
  • Relationships:

Area Scale Factor = (Length Scale Factor)2

Length Scale Factor = √(Area Scale Factor)

Volume Scale Factor = (Length Scale Factor)3

Length Scale Factor = ∛(Volume Scale Factor)

Request for Demo Lesson

Exam Tips

  • When conducting calculations, it is crucial to take extra care not to mix up the identities of the shapes involved. To maintain clarity, consider the following guidelines:

While doing calculations, it is important to be extra careful not to mingle and merge the identities of the figures. To maintain clarity, consider the following guidelines:

  1. Labelling Shapes:
    • Assign distinct labels to each shape involved in the comparison.
  2. Equation Representation:

    • All the time make equations to get clarity and for a perfect understanding.

For example:

If shape A is deemed similar to shape B, ensure the following relationships are maintained:

    • The length of shape A is represented as k times the length of shape B:

Length A = k (length B)

    • The area of shape A is correlated with the area of shape B by a factor of k2 :

area A = k2 (area B)

    • The volume of shape A is connected to the volume of shape B through a factor of k3:

Volume A = k3 (Volume B)

certified Physics and Maths tutor

 

 

Solved Example:

Question 1:

Solid P and solid Q are mathematically similar.

The volume of solid P is 32 cm3

The volume of solid Q is 108 cm3.

The height of solid P is 10 cm.

Find the height of solid Q.

Solution: 

Calculate k3, the scale factor of enlargement for the volumes, using Q = k3 (volume P), Or

k3 = large volume/smaller volume

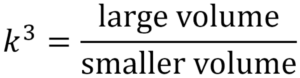
Area and Volume Questions

108 = 32k3

K3 = 108/32 = 27/8

For similar shapes, If the volume scale factor is k3 for similar shapes, then the length scale factor is k.

Find k.

Similar Shapes Questions

Substitute into the formula for the heights of similar shapes. Height Q = k(height P).

h = 10k

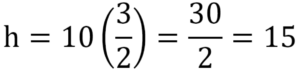
Similar Shapes Equation

Height of Q = 15 cm

The height of Solid Q is 15 cm.

Conclusion

  • Understanding similar shapes is of fundamental significance for various applications in mathematics, such as geometry and real-world examples.
  • The scaling factor sets in play corresponding proportional relationships between the sides, angles, area and volume of the shapes being related.
  • By specifying the practical examples, we have shown the efficiency of these fundamentals in processing the actual world problems similarly emphasizing the usefulness of similarity in mathematical modeling and analysis.

Worksheet on Similar Shapes

Question 1: Below are two similar triangles. Similar Shapes Right Angled Triangle The area of triangle P is 20cm2 Work out the area of triangle Q.



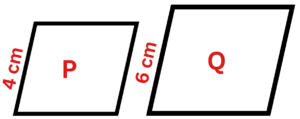
Question 2: Below are two similar parallelograms. Similar Shapes Worksheet Questions The area of parallelogram P is 28cm2 Work out the area of parallelogram Q



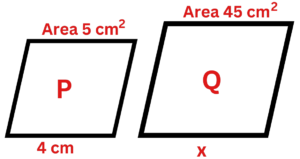
Question 3: Shown below are two mathematically similar parallelograms. Similar Shapes (Area and Volume) Find x.



Question 4: The areas of two mathematically similar shapes are in the ratio 49:81 The length of the smaller shape is 24.5cm Work out the length of the larger shape..