Quadratic Formula Questions with Step-by-Step Examples

Calculator
Test Yourself

Quadratic Formula

  • Quadratic equations are an essential concept in algebra, used to solve a variety of problems in mathematics and real-world applications.
  • In order to solve a quadratic equation, the quadratic formula is used.

In this article, we will discuss: 

  1. What is a Quadratic Formula?
  2. What is a Discriminant?
  3. Steps for Solving a Quadratic Equation with Quadratic Formula

Here is one more link to practice a few extra questions: Maths Genie Quadratic Formula Questions

What is a Quadratic Equation?

  • A quadratic equation is a polynomial equation of the second degree, which can be represented in the form

ax² + bx + c = 0,

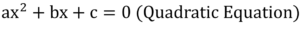
Quadratic Equation Formula

where a, b, and c are constants, and x is the variable.

  • The equation has one variable, which is squared, and this is what makes it quadratic.
  • A quadratic equation can have two solutions, one solution or no real solution, depending on the values of a, b, and c.

What is a Quadratic Formula?

  •  The quadratic formula is a formula used to solve a quadratic equation.
  • The formula is given by:

x = (-b ± √(b² – 4ac))/2a

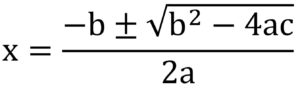
Quadratic Formula is a formula used to solve a quadratic equation

  • where a, b, and c are the coefficients of the quadratic equation ax² + bx + c = 0.
  • The formula provides the values of x, which are the solutions to the quadratic equation. The quadratic formula can be used for all quadratic equations, regardless of the values of a, b, and c.

What is a Discriminant?

  • The discriminant is a value that is used to determine the number and type of roots of a quadratic equation.
  • The discriminant is given by the expression

b2 – 4ac

Quadratic Formula Discriminant

Which is part of the quadratic formula.

  • The value of the discriminant can be positive, negative, or zero.

Conditions for Equal, Distinct, and Real Roots for Discriminant

  • The value of the discriminant determines the nature of the roots of a quadratic equation.
  • The following conditions hold:

(a) If the discriminant is positive, the roots are distinct and real.

b2 – 4ac > 0

Quadratic Formula discriminant is positive, the roots are distinct and real

(b) If the discriminant is zero, the roots are equal and real.

b2 – 4ac = 0

Quadratic Formula discriminant is zero, the roots are equal and real.

(c) If the discriminant is negative, the roots are imaginary, and the equation has no real solutions.

b2 – 4ac < 0

The Discriminant is negative, the roots are imaginary, and the equation has no real solutions.

Steps for Solving a Quadratic Equation with Quadratic Formula

  • The steps for solving a quadratic equation using the quadratic formula are as follows:

Step #1: Write the quadratic equation in the form ax² + bx + c = 0.

Step #2: Identify the values of a, b, and c.

Step #3: Calculate the discriminant using the formula b² – 4ac.

Step #4: Determine the nature of the roots using the conditions for the discriminant.

Step #5: If the roots are distinct and real, substitute the values of a, b, and c in the quadratic formula, and simplify to get the solutions.

Step #6: If the roots are equal and real, substitute the values of a, b, and c in the quadratic formula, and simplify to get the solution.

Step #7: If the roots are imaginary, the quadratic equation has no real solutions.

certified Physics and Maths tutor

 

 

Solved Example: 

Question 1: Solve the quadratic equation x² – 3x – 10 = 0 using the quadratic formula.

Solution: 

  • Step #1: Write the equation in the standard form ax² + bx + c = 0.

    x² – 3x – 10 = 0

  • Step #2: Identify the values of a, b, and c.

    a = 1, b = -3, c = -10

  • Step #3: Substitute the values of a, b, and c into the quadratic formula:

    x = (-b ± √b² – 4ac)/2a

    x = (3 ± √(3² – 4(1)(-10))/2(1)

  • Step #4: Simplify the expression inside the square root:

    x = (3 ± √(49))/2

  • Step #5: Solve for x:

x1 = (3 + 7)/2 = 5

x2 = (3 – 7)/2 = -2

Therefore, the solutions to the equation x² – 3x – 10 = 0 are x = 5 and x = -2.

 

Question 2: Solve the quadratic equation 4x² – 5x + 1 = 0 using the quadratic formula.

Solution: 

  • Step #1: Write the equation in the standard form ax² + bx + c = 0.

    4x² – 5x + 1 = 0

  • Step #2: Identify the values of a, b, and c.

    a = 4, b = -5, c = 1

  • Step #3: Substitute the values of a, b, and c into the quadratic formula:

    x = (-b ± √b² – 4ac)/2a

    x = (5 ± √(5² – 4(4)(1))/2(4)

  • Step #4: Simplify the expression inside the square root:

    x = (5 ± √(9))/8

  • Step #5: Solve for x:

x1 = (5 + 3) / 8 = 1

x2 = (5 – 3) / 8 = 0.25

Therefore, the solutions to the equation 4x² – 5x + 1 = 0 are x = 1 and x ≈ 0.25.

Request for Demo Lesson

Practice Questions

Question 1. Solve the quadratic equation x2 + 2x – 15 = 0 using the quadratic formula.

Answer : ( , )


Question 2: Solve the quadratic equation x2 + 4x – 5 = 0 using the quadratic formula.

Answer : ( , )

Conclusion

  • In conclusion, the quadratic formula is a powerful and widely used tool in mathematics for solving quadratic equations.
  • It offers a reliable method to find the roots of quadratic equations, even in cases where factoring or other methods may not be applicable.
  • The quadratic formula is essential in various fields, including physics, engineering, finance, and computer science. Understanding and applying the quadratic formula accurately and efficiently is crucial for solving quadratic equations with precision.
  • The discriminant, represented by b² – 4ac, helps determine the nature of the roots—whether they are distinct and real, equal and real, or imaginary.

Worksheet on Quadratic Formula

Question 1: Solve the quadratic equation 2x2 + 5x - 3 = 0.

)

Question 2: Solve the quadratic equation 2x2 + 7x + 3 = 0.

)

Question 3: Solve the quadratic equation 2x2 - 3x + 1 = 0.

)

Question 4: Solve the quadratic equation x2 - 6x + 8 = 0.

)

Question 5: Solve the quadratic equation 2x2 - 3x - 5 = 0.

)