Pythagoras Theorem – GCSE Maths

Practice Questions
Downloads

Introduction

  • The Pythagorean Theorem is a simple rule that helps us figure out the length of one side in a right-angled triangle if we know the other two.
  • It is one of the most fundamental and well-known principles in geometry.
  • It is widely used in mathematics, physics, engineering, and everyday problem-solving to calculate distances or unknown side lengths.

Real-Life Application:

Uses of Pythagoras Theorem in construction, architecture, navigation, air traffic control

What is Pythagoras Theorem?

  • In a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
  • Mathematically, if a right-angled triangle has sides of lengths a, b, and c (where c is the hypotenuse), then:

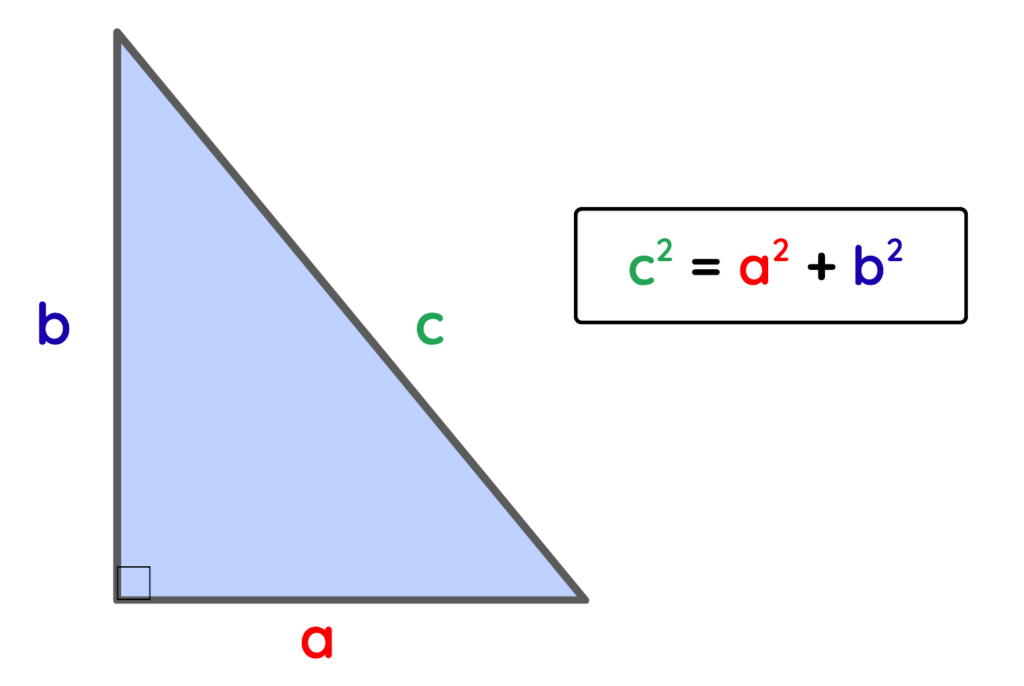
Pythagoras theorem formula c² = a² + b² with labelled right angle triangle

Key points:

  • Applies Only to Right-Angled Triangles
  • Hypotenuse is the Longest Side
  • It helps to find the length of any side when the other two are known.

certified Physics and Maths tutorSolved Example

Problem: A triangle has one side 6 cm long, another side 8 cm long, and a right angle between them. What is the length of the hypotenuse?

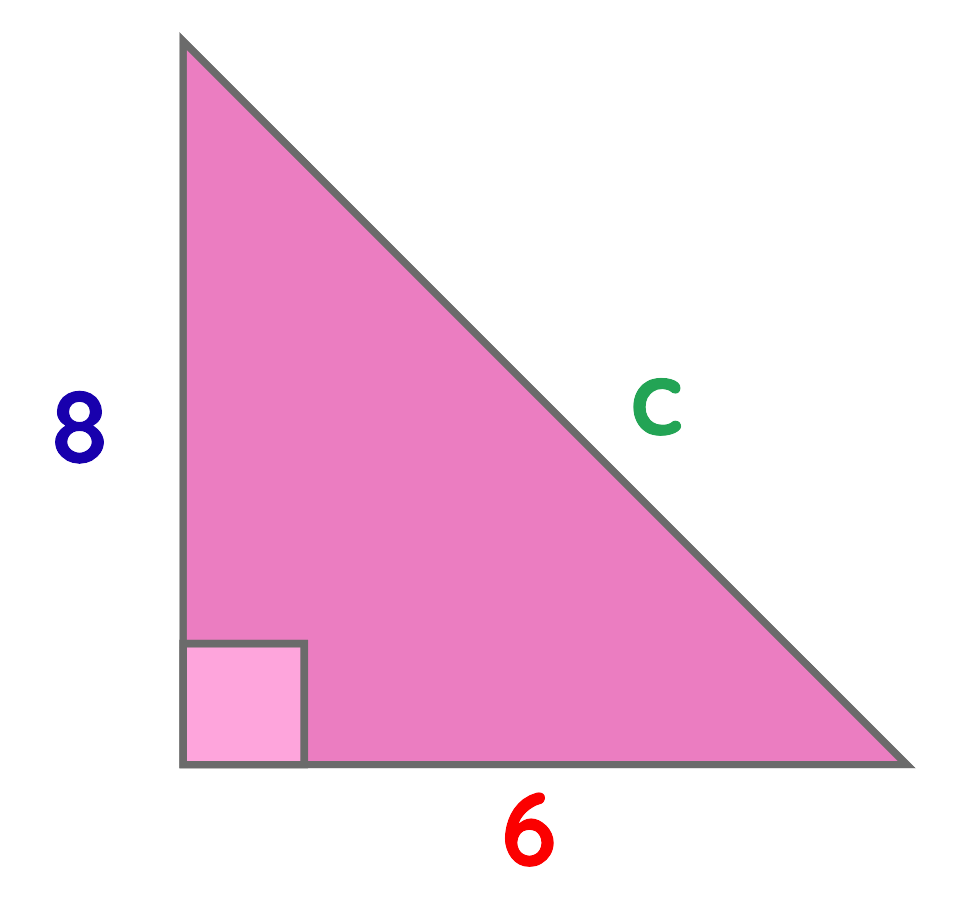
Right angle triangle with sides 6 and 8 for Pythagoras theorem calculation

Solution: 

Step #1: Given

    • Base a = 6 cm
    • Height b = 8 cm

Step #2: Using the formula:

Formula of Pythagoras theorem showing c squared equals a squared plus b squared

Step #3: Plug the values:

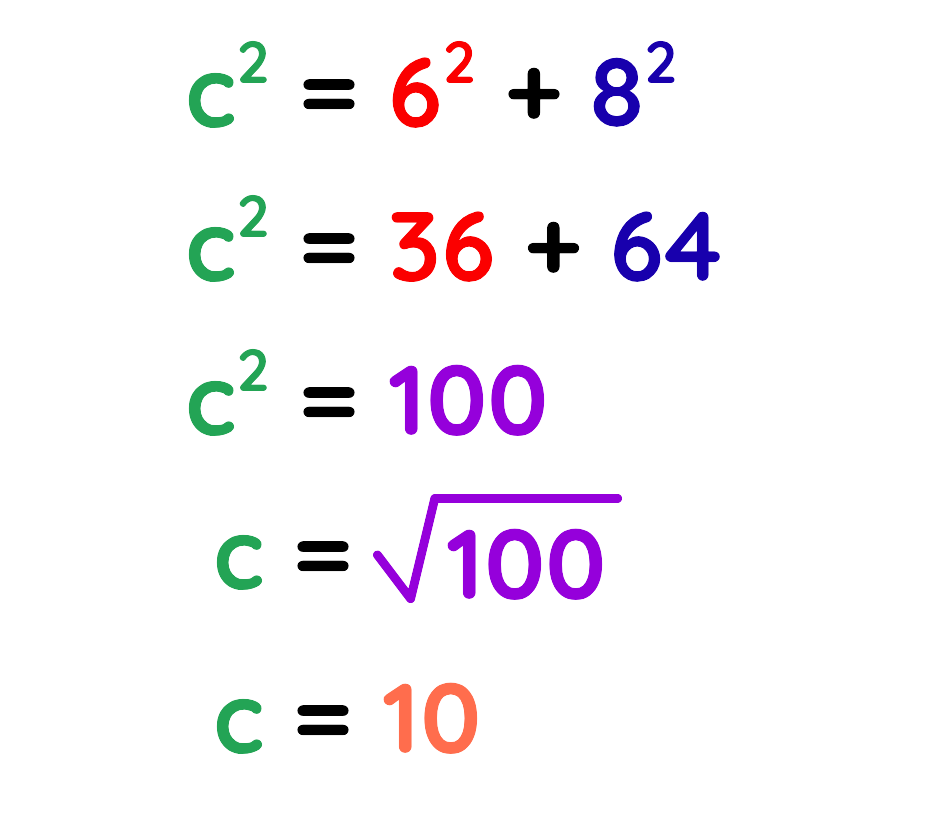
Step by step calculation using Pythagoras theorem to find hypotenuse

Final Answer: C = 10 cm

How To Find The Length of The Missing Side in a Right-Angled Triangle?

  • The Pythagorean Theorem helps find a missing side in a right-angled triangle when two sides are known.

Steps to Find Missing Sides in a Right-Angled Triangle:

  • Step#1: Identify the given sides
  • Step#2: Use the formula
  • Step#3: Plug the values
  • Step#4: Solve for the unknown side.

certified Physics and Maths tutorSolved Example

Problem: A right-angled triangle has one side 9 cm and another side 12 cm. What is the length of the hypotenuse?

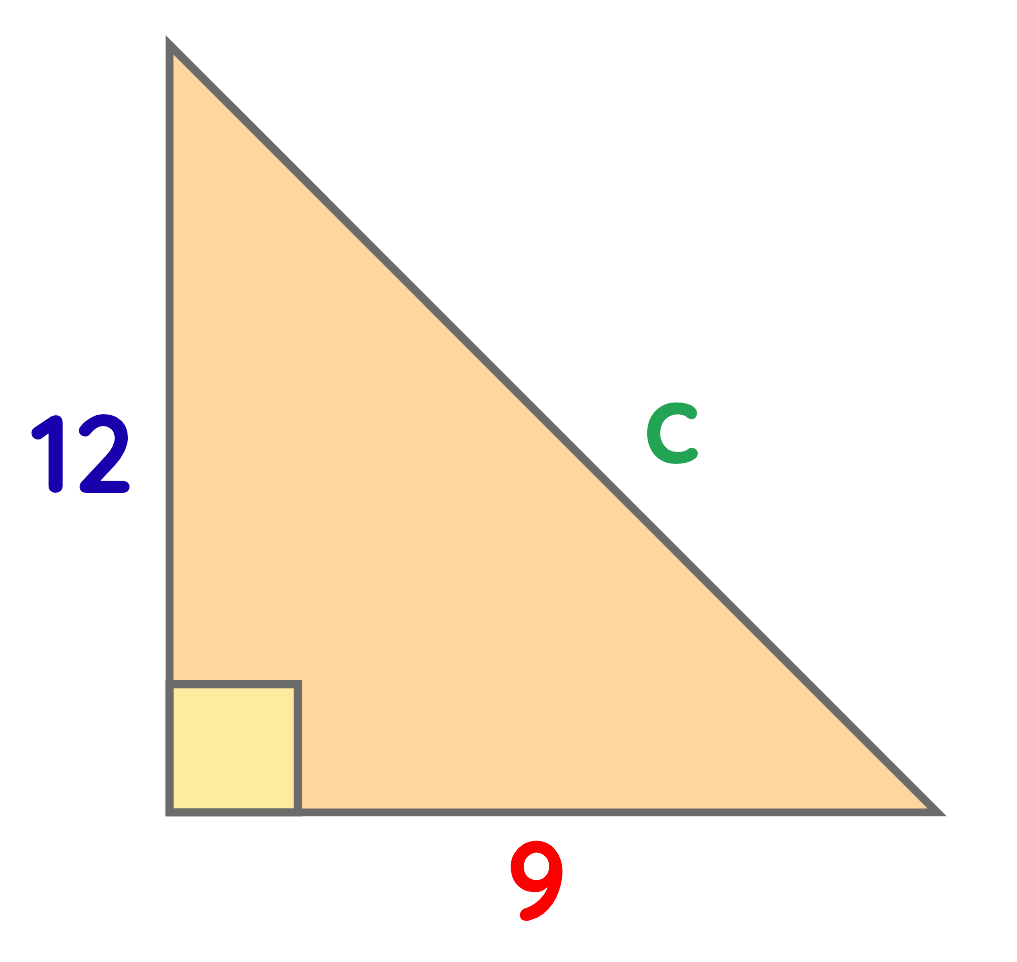
Right angled triangle with sides 9 cm and 12 cm to find hypotenuse using Pythagoras theorem

Solution: 

Step#1: Identify the Given Sides:

    • Base a = 9 cm
    • Height b = 12 cm

Step#2: Use The Formula:

Formula of Pythagoras theorem showing c squared equals a squared plus b squared

Step#3: Plug the values:

Equation showing c squared equals 9 squared plus 12 squared using Pythagoras theorem

Step#4: Solve for the unknown side:

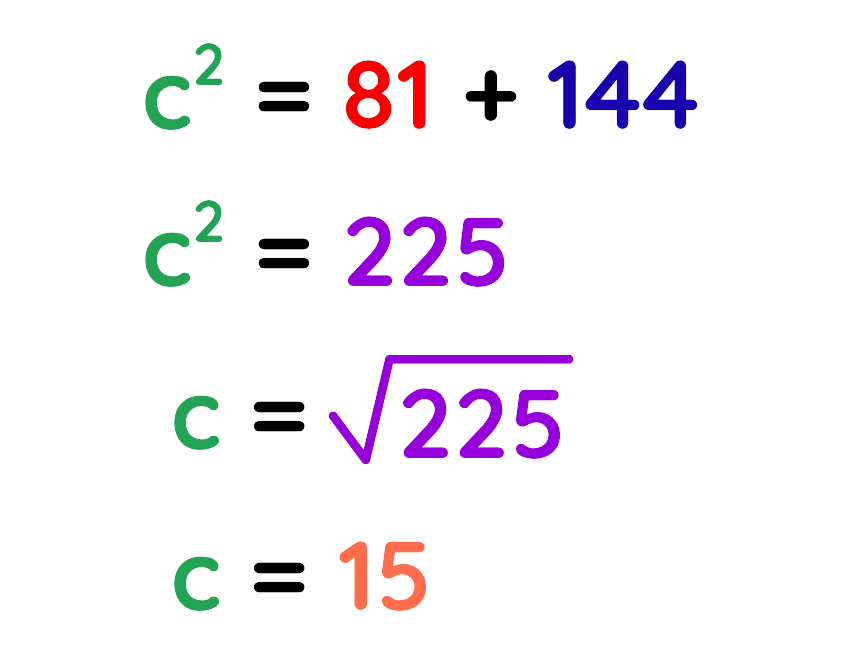
Pythagoras theorem calculation showing c squared equals 81 plus 144 equals 225 square root is 15

Final Answer: C = 15 cm

certified Physics and Maths tutorSolved Example

Problem: In a right-angled triangle, the base is 7 cm and the height is 24 cm. Find the length of the hypotenuse.

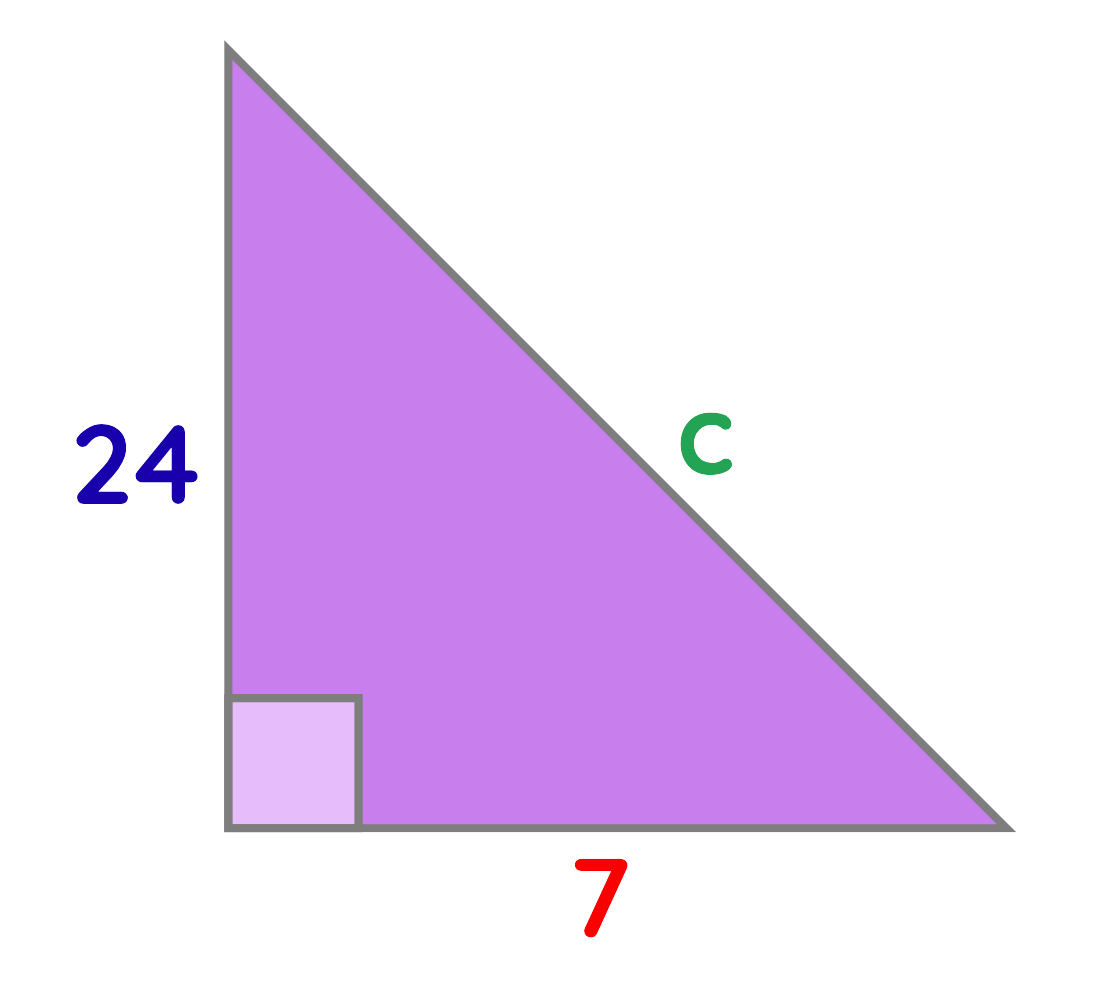
Right-angled triangle with sides 7 cm and 24 cm to find hypotenuse using Pythagoras theorem

Solution: 

Step#1: Identify the Given Sides:

    • Base a = 7 cm
    • Height b = 24 cm

Step#2: Use The Formula:

Formula of Pythagoras theorem showing c squared equals a squared plus b squared

Step#3: Plug the values:

Pythagoras theorem formula showing c squared equals 7 squared plus 24 squared

Step#4: Solve for the unknown side:

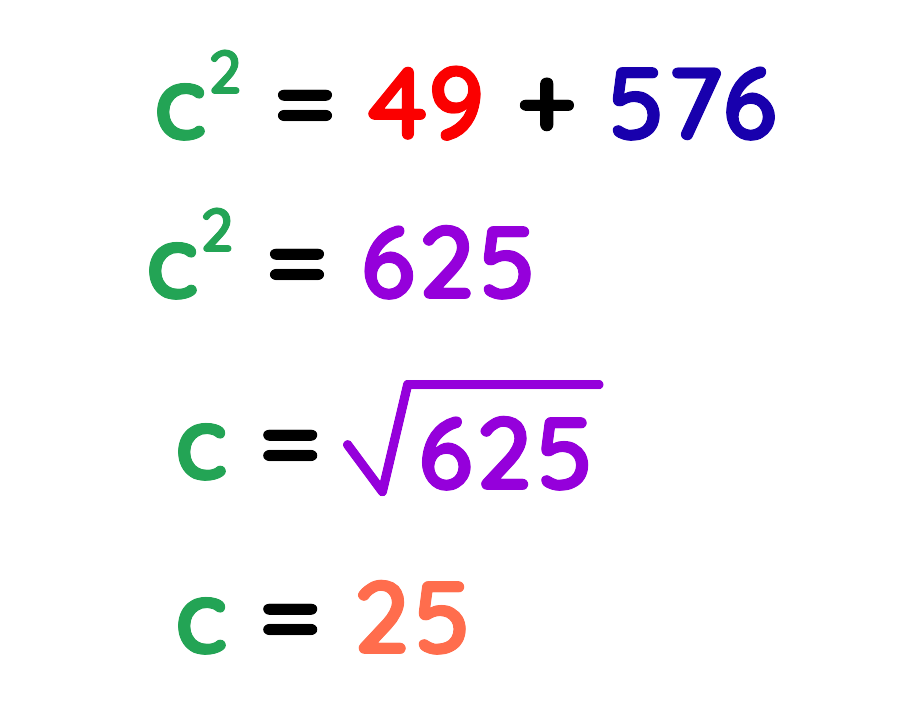
Pythagoras theorem calculation showing c squared equals 625 and c equals 25

Final Answer: C = 25 cm

certified Physics and Maths tutorSolved Example

Problem: A right-angled triangle has a hypotenuse of 13 cm and one side of 5 cm. What is the length of the other side?

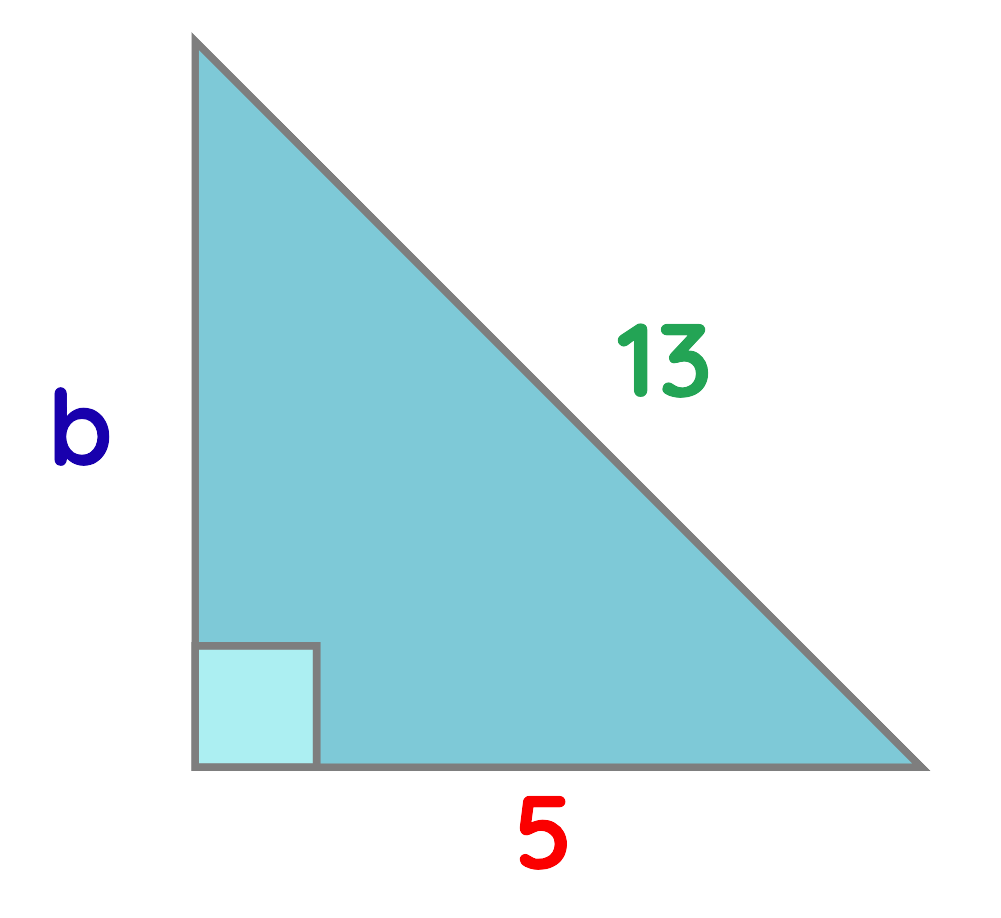
Right angled triangle with sides 5 and 13, finding the missing side b using Pythagoras theorem

Solution: 

Step#1: Identify the Given Sides:

    • Base a = 5 cm
    • Hypotenuse c = 13 cm

Step#2: Use The Formula:

Formula of Pythagoras theorem showing c squared equals a squared plus b squared

Rearrange it,

Rearranged Pythagoras theorem formula to find side b squared equals c squared minus a squared

Step#3: Plug the values:

Example of Pythagoras theorem showing b squared equals 13 squared minus 5 squared

Step#4: Solve for the unknown side:

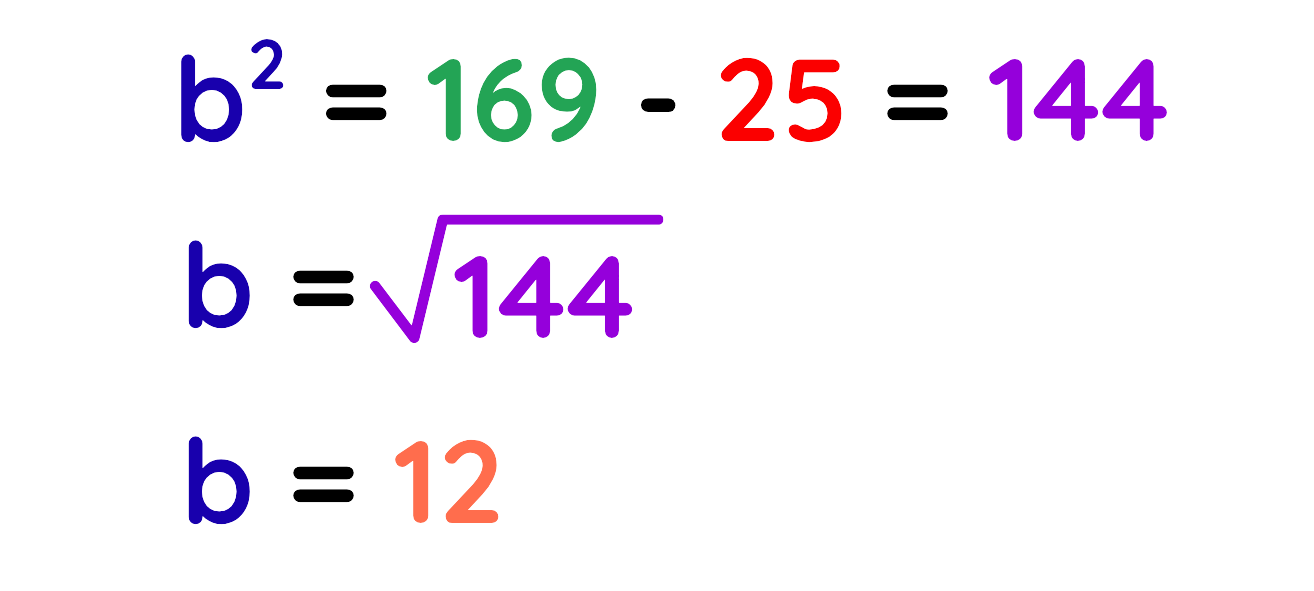
Pythagoras theorem worked example showing b equals square root of 144 equals 12

Final Answer: B = 12 cm

Table of Content

Join Tutoring