Probability – GCSE Maths
Introduction
- Probability is a branch of mathematics that deals with calculating the likelihood of events occurring.
- Probability helps us measure and predict the chances of events happening in the real world like-
What is a Probability?
- Probability is a measure of how likely an event is to occur.
Probability Rules:
- Range of Probability – 0 ≤ P(E) ≤ 1
- Sum of Probabilities – For all outcomes in S, ∑P(E) =1.
- Complement Rule – P(not E) = 1 − P(E).
For an event E, probability P(E) is calculated as:
Solved Example
Solved ExampleProblem: A bag contains 3 red marbles, 4 green marbles and 3 blue marbles. If you pick one marble at random, what is the probability that it will be blue?
Solution:
Total number of marbles:
Probability of picking a blue marble:
The probability of picking a blue marble is 3/10
Final Answer: 3/10
What is an Experimental Probability?
- Experimental probability is the probability of an event based on actual experiments or observations.
- It is calculated by dividing the number of times the event occurs by the total number of trials performed.
- Mathematically,
Note: Theoretical Probability is calculated without doing an Experiment.
Solved Example
Problem: If we flip a coin 10 times and get these results:
- Heads: 6 times
- Tails: 4 times
What is the experimental probability of getting Heads?
Solution:
- Successful outcomes (Heads): 6
- Total flips: 10
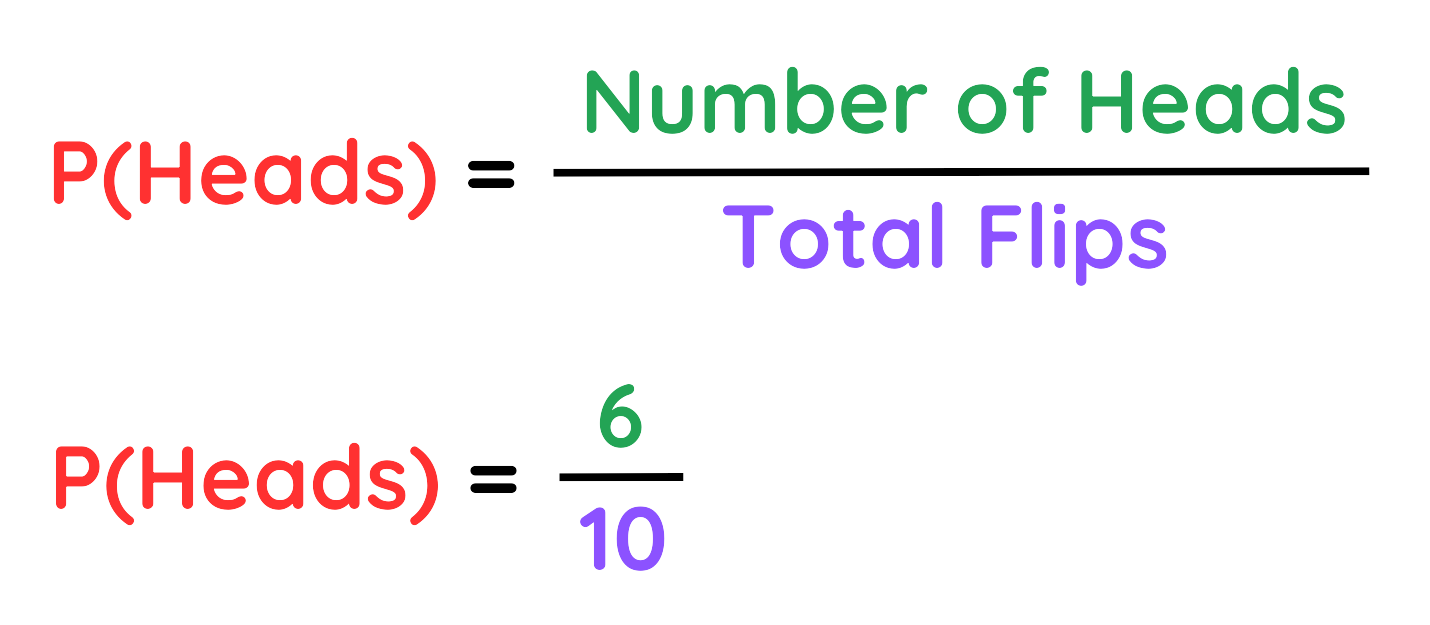
The experimental probability of getting Heads is 6/10
Final Answer: 6/10
Key Points
- Experiment: An experiment is any process that produces a well-defined outcome.
Examples:
- Outcome: An outcome is a possible result of an experiment.
Example: In a coin toss, Possible outcomes are Heads (H) or Tails (T).
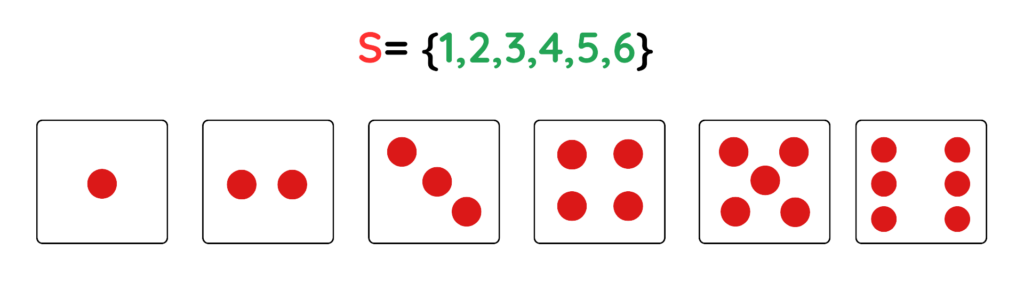
- Sample Space (S): The sample space is the set of all possible outcomes of an experiment.
Example: For a die roll,
- Events: An event is any subset of the sample space. It can include,
- Simple Event: A single outcome (e.g., rolling a 3).
- Compound Event: Multiple outcomes (e.g., rolling an even number {2,4,6}).
Solved Example
Problem: A coin is flipped 4 times. It lands on heads 3 times. What is the experimental probability of getting heads?
Solution:
The event is getting heads, where:
- Heads occurred 3 times.
- Total number of coin flips = 4.
Using the Experimental Formula:
So, the Experimental probability of getting heads is 0.75
Final Answer: 0.75
Solved Example
Problem: A bag has 5 red and 3 blue balls. One ball is picked. Find the probability that the ball is not blue.
Solution:
Given:
- Total Balls = 5 + 3 = 8
- Blue balls = 3
Use the complement rule:
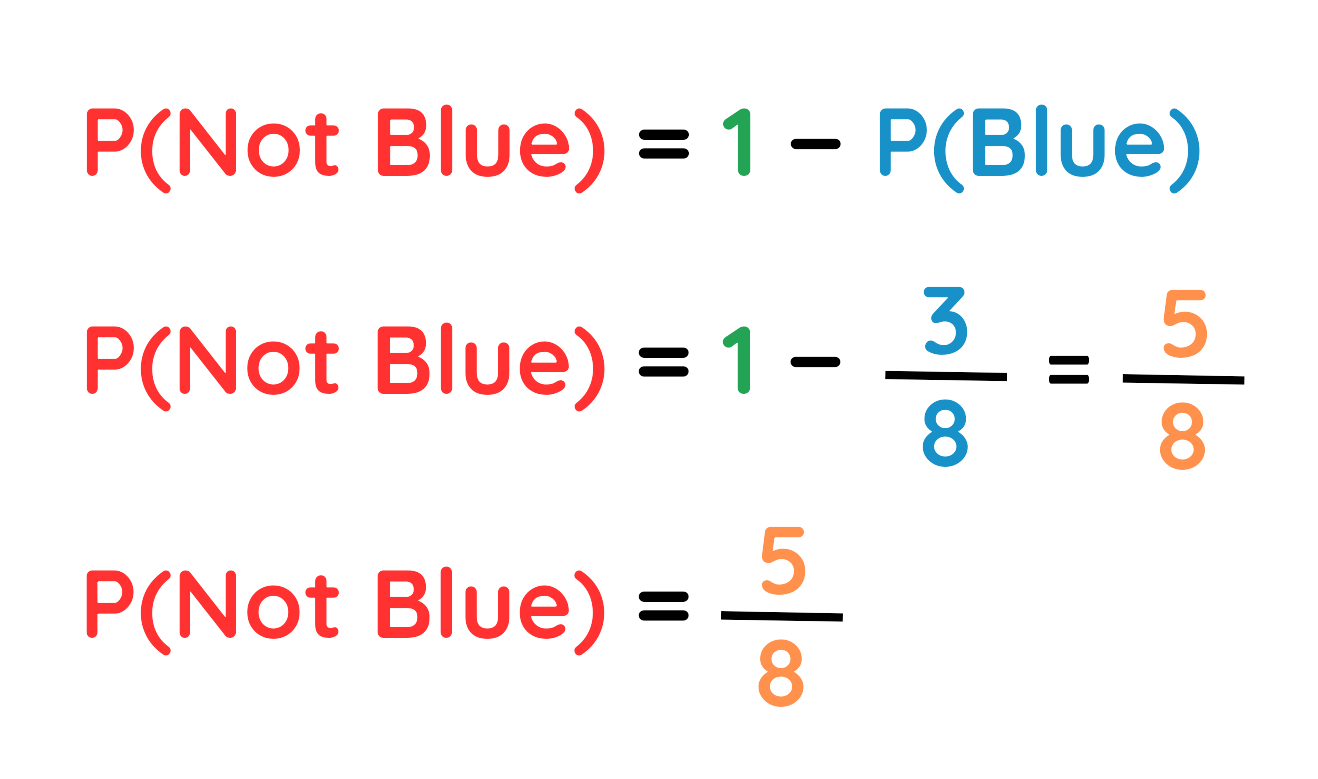
The probability that the ball is not blue is 5/8
Final Answer: 5/8
Solved Example
Problem: A coin is tossed once. What is the probability of getting a head?
Solution:
Given:
- Total possible outcomes = 2 (Head, Tail)
Probability of getting a head:
The probability of getting a head 1/2
Final Answer: 1/2