Multiplying Algebraic Fractions | GCSE Maths

Practice Questions
Downloads

Introduction to Multiplying Algebraic Fractions

  • Algebraic fractions are fractions that contain algebraic expressions in the numerator, denominator, or both. Just like numerical fractions, they follow specific rules for addition, subtraction, multiplication, and division.
  • Among these operations, multiplication is often the easiest because it doesn’t require finding a common denominator. However, understanding simplification is crucial to solving problems efficiently.

What Skills Do You Need to Learn Before Multiplying Algebraic Fractions?

Before multiplying algebraic fractions, you should be familiar with the following key algebraic skills:

  • Factorisation – This helps simplify algebraic fractions before multiplication. For example, the quadratic expression:

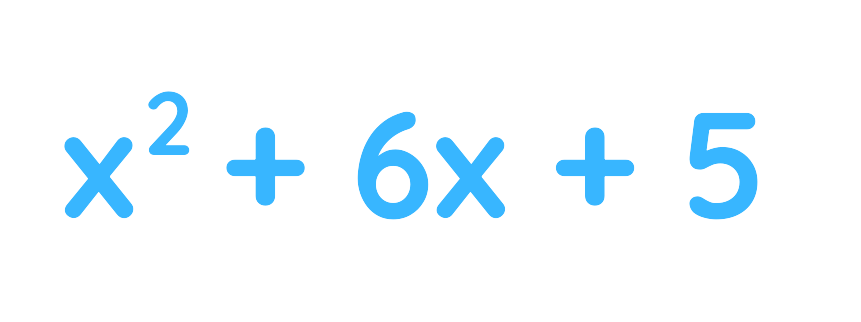
can be factorised as:

Factorisation allows us to cancel common terms easily when multiplying fractions.  Learn Factorisation

  • Basic Algebraic Manipulation – Expanding brackets, simplifying terms, and rearranging equations are fundamental. For instance:

Understanding these operations helps when working with algebraic expressions in fractions.  Learn Basic Algebraic Manipulation

  • Understanding Algebraic Fractions – Knowing how to simplify algebraic fractions before performing operations is essential. For example:

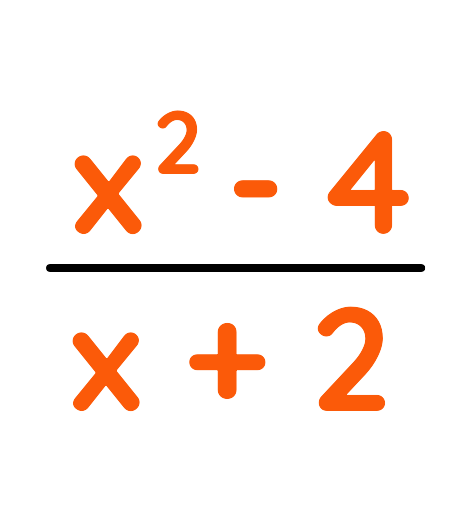
can be rewritten as:

Simplifying before multiplying makes calculations much easier. Learn Algebraic Fractions

If you’re unsure about any of these topics, click the links to review them before moving forward!

Steps for Multiplying Algebraic Fractions

  1. Multiplying algebraic fractions follows the same principles as multiplying numerical fractions. However, since algebraic expressions are involved, simplifying before multiplying is crucial.

Steps to Multiply Algebraic Fractions

1. Factorise the numerators and denominators (if possible) – This helps identify common terms that can be cancelled.

2. Cancel out any common factors – If a term appears in both the numerator and denominator, it can be removed.

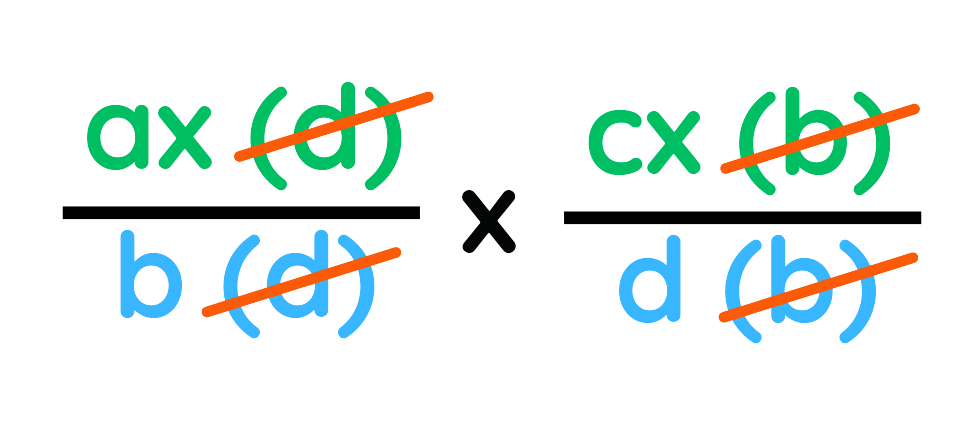
3. Multiply the remaining numerators together and multiply the remaining denominators together.

4. Simplify the final expression if necessary.

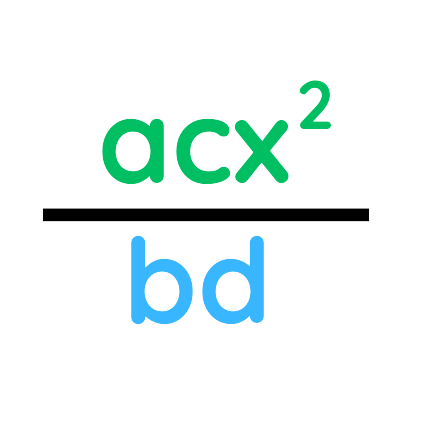
Key Rule to Remember:

  • Just like with numerical fractions, you multiply across the numerators and denominators after simplification.

Before moving ahead, make sure you’re confident in simplifying algebraic fractions. If you need a quick revision, check out our Simplifying Algebraic Fractions Guide.

Examples of Multiplying Algebraic Fractions

  • Now that we understand the steps, let’s go through some examples to see how to apply them in practice.

certified Physics and Maths tutorSolved Example: Basic Multiplication

Problem:

Multiplication of two algebraic fractions, represented as (2x / 3) × (5 / 4x).

Solution: 

Step #1: Identify Common Factors:

The variable x appears in both the numerator and denominator.

Step #2: Cancel Common Factors:

Now, multiply across:

Multiplication of fractions (2 × 5) / (3 × 4) showing the result as 10 / 12.

Step #3: Simplify the fraction:

Simplification of the fraction 10/12 to its lowest terms, 5/6.

Final Answer: 5/6

certified Physics and Maths tutorSolved Example: Multiplication with Factorisation

Problem: 

Solution: 

Step #1: Factorise Where Possible:

The numerator x2 − 1 is a difference of squares:

Rewrite the fractions:

Step #2: Cancel Common Factors:

    • x + 4 cancels out.
    • x − 1 cancels out.

Step #2: Multiply the Remaining Terms:

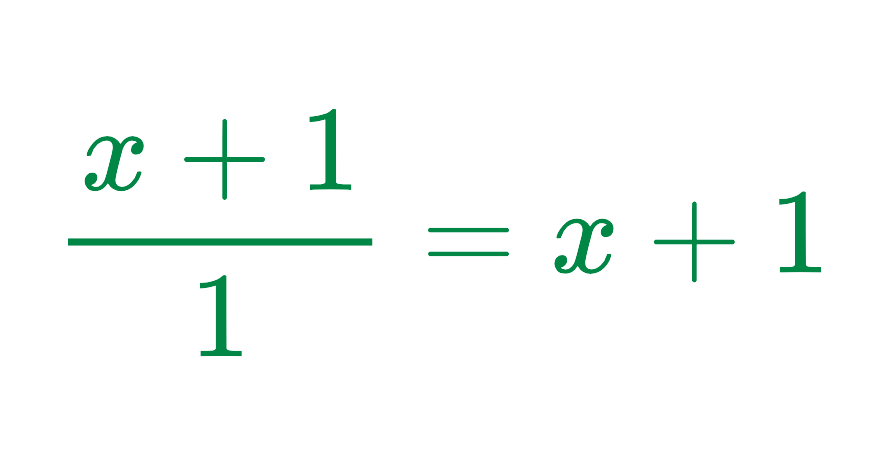
Final Answer: x + 1

certified Physics and Maths tutorSolved Example: Multiplying More Complex Expressions

Problem: 

Solution: 

Step #1: Factorise Where Possible:

The numerator x2 − 9 is a difference of squares:

The denominator x2 − 4 is also a difference of squares:

Rewriting the expression:

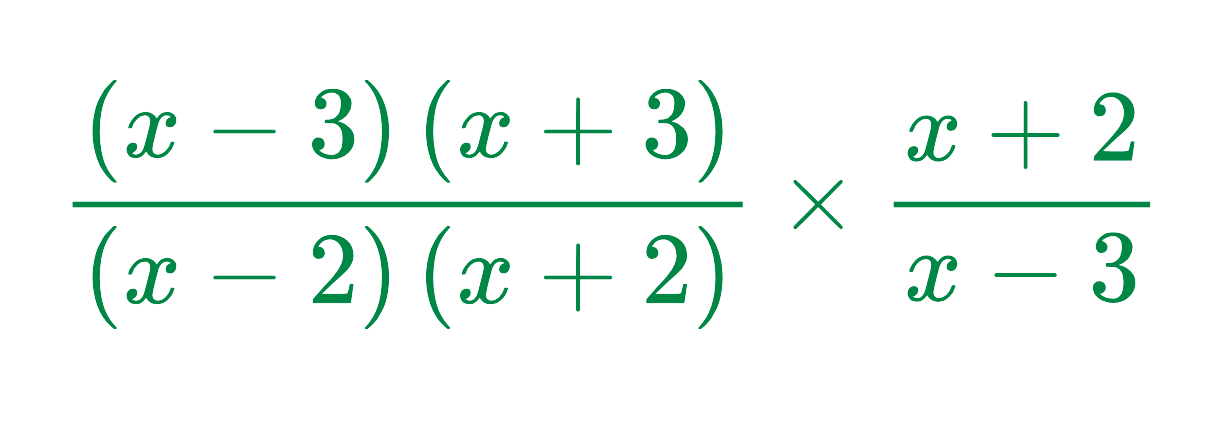
Step #2: Cancel Common Factors:

    • x – 3 cancels out.
    • x + 2 cancels out.

Step #2: Multiply the Remaining Terms:

Final Answer: x + 3 / x – 2

If you’re struggling with factorisation, check out our Factorisation Guide to master this skill before moving ahead.

Common Mistakes & How to Avoid Them

When multiplying algebraic fractions, students often make errors that lead to incorrect answers. Below are the most common mistakes and how to avoid them.

certified Physics and Maths tutorMistake 1: Directly Multiplying Without Factorising (Biggest Mistake!)

Problem: 

Incorrect Approach:

Some students multiply directly without factorising, like this:

Expanding incorrectly:

This makes the expression unnecessarily complicated and difficult to simplify later. This is the biggest mistake students make!:

Correct Approach:

Factorise first:

    • x2 − 9 is a difference of squares:

    • x2 − 4 is also a difference of squares:

Now, rewrite the expression:

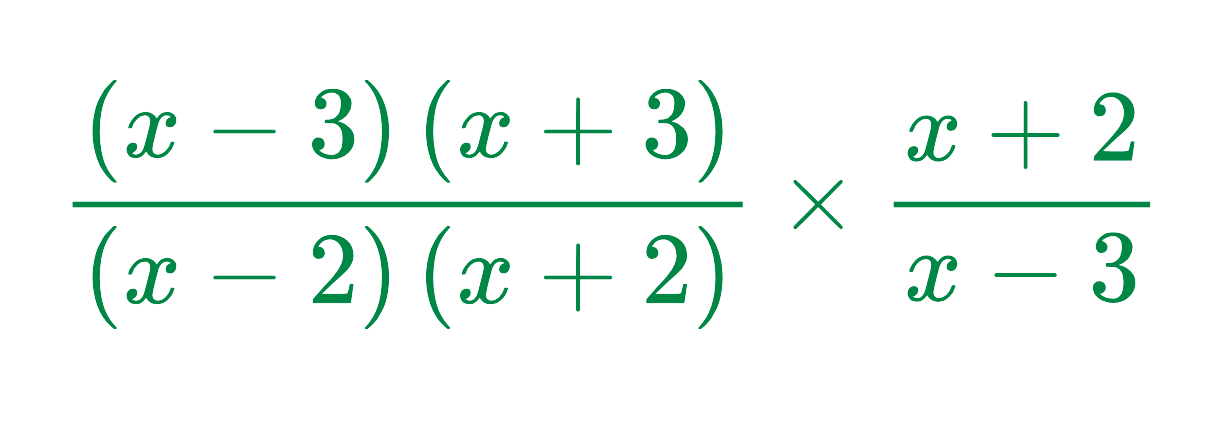
Now, cancel the common factors:

    • x − 3 cancels out.
    • x + 2 cancels out.

Final Answer: x + 3 / x – 2

💡 Tip: Never multiply directly! Always factorise first to simplify your work.

certified Physics and Maths tutorMistake 2: Not Cancelling Common Factors Properly

Problem:

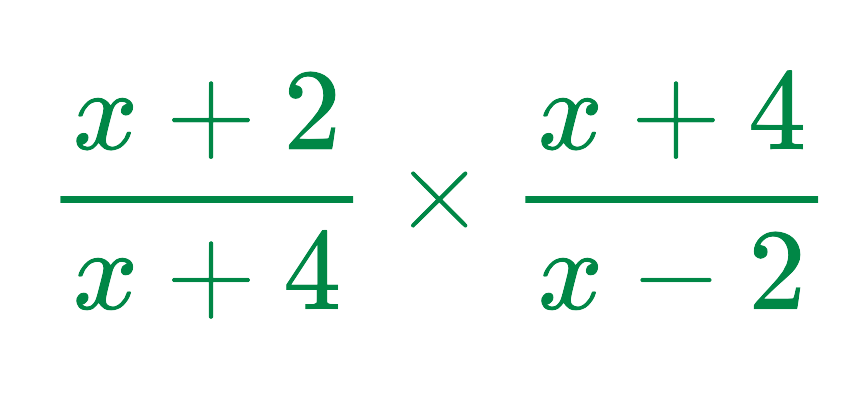
Incorrect Approach:

Some students multiply first:

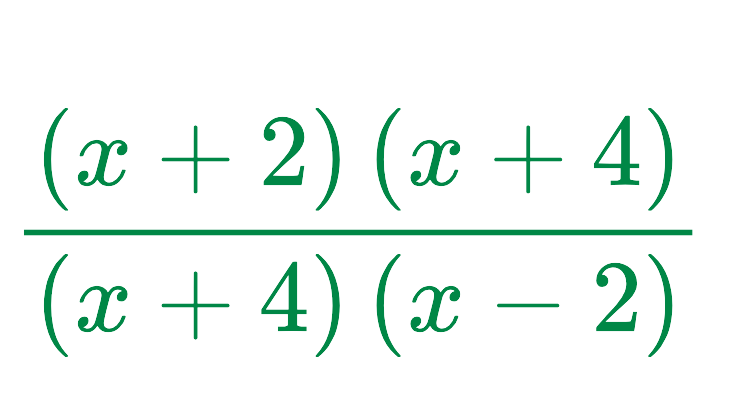
Then cancel after multiplying, which creates extra steps.

Correct Approach:

Cancel common terms before multiplying:

Now, multiply:

Final Answer: x + 2 / x – 2

💡 Tip: Cancel terms before multiplying to simplify your work.

certified Physics and Maths tutorMistake 3: Incorrect Multiplication of Numerators and Denominators

Problem:

Incorrect Approach:

Some students incorrectly add denominators instead of multiplying:

This is wrong because denominators should be multiplied, not added.

Correct Approach:

Multiply properly:

Final Answer: 

💡 Tip: Always multiply numerators together and denominators together. Never add denominators!

Final Tip: Always Check Your Final Answer

Before finalizing your answer, always check:

  • Did you factorise everything possible?
  • Did you cancel correctly?
  • Is your final answer in its simplest form?

Need extra practice? Check out our Multiplying Algebraic Fractions Worksheet for more questions!

Practice Questions and Answers on Multiplying Algebraic Fractions

  • Now that you’ve learned how to multiply algebraic fractions, it’s time to test your understanding! Try solving these GCSE-style questions, making sure to factorise and simplify where possible.

Question 1: Multiply and simplify:

(3x / 5) × (10 / 6x)

Question 2: Multiply and simplify:

(x² – 16) / (x + 4) × (x + 4) / (x – 4)

Question 3: Multiply and simplify:

(x² + 7x + 12) / (x + 3) × (x + 2) / (x + 4)

Question 4:Multiply and simplify:

(x² – 9) / (x² – 1) × (x + 1) / (x – 3)

Question 5: Multiply and simplify:

(x² + 5x + 6) / (x² – 4) × (x – 2) / (x + 3)

Question 6: Multiply and simplify:

(x² – 4x + 4) / (x² – 5x + 6) × (x – 3) / (x – 2)

Question 7: Multiply and simplify:

(2x² – 18) / (x² – 9) × (x + 3) / (x – 3)

Question 8: Multiply and simplify:

(x³ – 8) / (x² – 4x + 4) × (x – 2) / (x + 2)

Question 9: Multiply and simplify:

(x² – 7x + 10) / (x² – x – 20) × (x + 4) / (x – 2)

Question 10: Multiply and simplify:

(x³ – x² – x + 1) / (x² – 1) × (x – 1) / (x + 1)

Want to Check Your Answers?

Download the Multiplying Algebraic Fractions Worksheet with Solutions to see step-by-step explanations for each question.

Need to revise? Check out our Full Guide on Algebraic Fractions before attempting these questions!

Solutions

Question 1: 

Solution:

Step 1: Identify Common Factors

      • 10 and 5 share a common factor of 5.
      • 6x and 3x share a common factor of 3x.

Step 2: Cancel Common Factors

(3x / 5) × (10 / 6x)

= ( 3x / 3x ) × ( 10 / 5 )

= (1 / 1) × (2 / 2)

Step 3: Multiply Remaining Terms

(1 × 2) / (1 × 2) = 2 / 2 = 1

Final Answer: 1

 

Question 2:

Solution:

Step 1: Factorise the Numerator

x² – 16 = (x – 4)(x + 4)

Rewrite the expression:

((x – 4)(x + 4)) / (x + 4) × (x + 4) / (x – 4)

Step 2: Cancel Common Factors

      • x + 4 cancels out.
      • x – 4 cancels out.

Final Answer: 1

 

Question 3:

Solution:

Step 1: Factorise the Numerator

x² + 7x + 12 = (x + 3)(x + 4)

Rewrite the expression:

((x + 3)(x + 4)) / (x + 3) × (x + 2) / (x + 4)

Step 2: Cancel Common Factors

      • x + 3 cancels out.
      • x + 4 cancels out.

Final Answer: x + 2

 

Question 4:

Solution:

Step 1: Factorise

x² – 9 = (x – 3)(x + 3)

x² – 1 = (x – 1)(x + 1)

Rewrite the expression:

((x – 3)(x + 3)) / ((x – 1)(x + 1)) × (x + 1) / (x – 3)

Step 2: Cancel Common Factors

      • x – 3 cancels out.
      • x + 1 cancels out.

Final Answer: (x + 3) / (x – 1)

 

Question 5: 

Solution:

Step 1: Factorise

x² + 5x + 6 = (x + 3)(x + 2)

x² – 4 = (x – 2)(x + 2)

Rewrite the expression:

((x + 3)(x + 2)) / ((x – 2)(x + 2)) × (x – 2) / (x + 3)

Step 2: Cancel Common Factors

      • x + 3 cancels out.
      • x – 2 cancels out.
      • x + 2 cancels out.

Final Answer: 1

 

Question 6: 

Solution:

Step 1: Factorise

x² – 4x + 4 = (x – 2)(x – 2)

x² – 5x + 6 = (x – 3)(x – 2)

Rewrite the expression:

((x – 2)(x – 2)) / ((x – 3)(x – 2)) × (x – 3) / (x – 2)

Step 2: Cancel Common Factors

      • x – 2 cancels out (twice).
      • x – 3 cancels out.

Final Answer: 1

 

Question 7: 

Solution:

Step 1: Factor out the common factors

2x² – 18 = 2(x² – 9) = 2(x – 3)(x + 3)

x² – 9 = (x – 3)(x + 3)

Rewrite the expression:

(2(x – 3)(x + 3)) / ((x – 3)(x + 3)) × (x + 3) / (x – 3)

Step 2: Cancel Common Factors

      • x – 3 cancels out.
      • x + 3 cancels out.

Final Answer: 2

 

Question 8: 

Solution:

Step 1: Factorise

x³ – 8 = (x – 2)(x² + 2x + 4)

x² – 4x + 4 = (x – 2)(x – 2)

Rewrite the expression:

((x – 2)(x² + 2x + 4)) / ((x – 2)(x – 2)) × (x – 2) / (x + 2)

Step 2: Cancel Common Factors

      • x – 2 cancels out (twice).

Final Answer: (x² + 2x + 4) / (x + 2)

 

Question 9: 

Solution:

Step 1: Factorise

x² – 7x + 10 = (x – 5)(x – 2)

x² – x – 20 = (x – 5)(x + 4)

Rewrite the expression:

((x – 5)(x – 2)) / ((x – 5)(x + 4)) × (x + 4) / (x – 2)

Step 2: Cancel Common Factors

      • x – 5 cancels out.
      • x – 2 cancels out.
      • x + 4 cancels out.

Final Answer: 1

 

Question 10: 

Solution:

Step 1: Factorise

x² – 1 = (x – 1)(x + 1)

Rewrite the expression:

(x³ – x² – x + 1) / ((x – 1)(x + 1)) × (x – 1) / (x + 1)

Step 2: Cancel Common Factors

      • x – 1 cancels out.
      • x + 1 cancels out.

Final Answer: x² – x + 1

Request for Demo Lesson

Table of Content