Inequalities on a Number Line: Examples with Practice Questions

In this article, we will discuss how to solve inequalities and represent them on a number line.

Practice Questions
Downloads

Video Tutorial on GCSE  Maths: Inequalities on a Number Line

  • Watch this Video Tutorial as we explain all types of Inequalities on a Number Line for GCSE Maths.

Inequalities on a Number Line

Inequalities are fundamental in algebra and help us understand the range of possible values that satisfy a condition.

We will discuss are:

  • The Basic Inequality Symbols
  • How to plot them on a number line
  • Work through examples
  • Including compound inequalities.

They are very important in practicing questions for coordinate geometry as well.

Here is one more link to practice a few extra questions: Maths Genie Inequalities on a Number Line Questions

Understanding Inequality Symbols

Inequalities express a relationship where two values are not equal and one is greater or lesser than the other. The primary inequality symbols are:

  • Less than (<): Indicates that one value is smaller than another.
  • Greater than (>): Indicates that one value is larger than another.
  • Less than or equal to (≤): Indicates that one value is smaller than or equal to another.
  • Greater than or equal to (≥): Indicates that one value is larger than or equal to another.

Representing Inequalities on a Number Line

A number line is a visual tool that helps illustrate the set of values that satisfy an inequality.

Key Steps to Plot an Inequality:

  1. Draw a Number Line: Sketch a horizontal line and mark relevant numbers.
  2. Identify Key Points: Mark the number(s) involved in the inequality.
  3. Use Circles to Indicate Inclusion:
    • Open Circle: Used when the number is not included in the solution (for < or >).
    • Closed Circle: Used when the number is included in the solution (for ≤ or ≥).

4. Shade the Solution Area:

    • Draw an arrow or line extending left or right to represent all possible values that satisfy the inequality.

certified Physics and Maths tutor

 

 

Solved Example 1

Question: x<5

Solution: 

Interpretation:

  • x can be any number less than 5 (e.g., 4, 0, -3, 4.9).

Steps to Plot:

Step 1: Draw a number line and label key points, including 5.

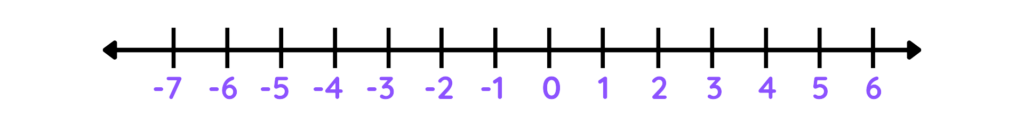
Number line labeled from -7 to 6, used for plotting inequalities in algebra.

Step 2: Place an open circle at 5 because 5 is not included.

Number line with an open circle at 5 indicating that 5 is not included in the inequality.

Step 3: Shade the line to the left of 5, indicating all numbers less than 5.

Number line shaded to the left of 5 with an open circle at 5 indicating all numbers less than 5.

certified Physics and Maths tutor

 

 

Solved Example 2

Question: x>5

Solution: 

Interpretation:

  • x can be any number greater than 5 (e.g., 6, 7, 5.1).

Steps to Plot:

Step 1: Draw a number line and mark the point 5.

Number line labeled from 0 to 13 with a mark at 5.

Step 2: Place an open circle at 5.

Number line with an open circle at 5, indicating the number is not included in the solution.

Step 3: Shade the line to the right of 5, showing all numbers greater than 5.

Number line showing values greater than 5 with an open circle and arrow pointing to the right.

Including the Endpoint

  • When the inequality includes equality (≤ or ≥), the endpoint is part of the solution set.

certified Physics and Maths tutor

 

 

Solved Example 3:

Question: x ≤ 5

Solution: 

Interpretation:

  • x can be 5 or any number less than 5.

Steps to Plot:

Step 1: Draw a number line and label 5.

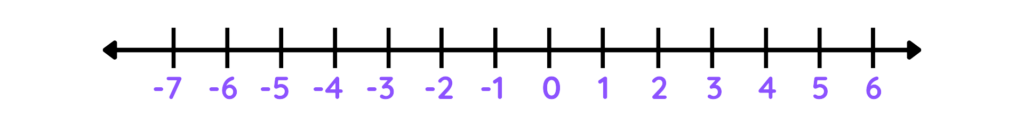
Number line labeled from -7 to 6, used for plotting inequalities in algebra.

Step 2: Place a closed circle at 5 to include it in the solution.

Number line with a closed circle at 5, indicating 5 is included in the solution.

Step 3: Shade the line to the left of 5.

Number line shaded to the left of 5, including 5 as a closed circle.

certified Physics and Maths tutor

 

 

Solved Example 4: 

Question: x ≥ 5

Solution: 

Interpretation:

  • x can be 5 or any number greater than 5.

Steps to Plot:

Step 1: Draw a number line and label 5.

Number line labeled from 0 to 13 with a mark at 5.

Step 2: Place a closed circle at 5.

Number line with a closed circle at 5.

Step 3: Shade the line to the right of 5.

Number line with a closed circle at 5 and shaded line to the right.

Summary of Symbols and Circles

  • Open Circle: Used for < and > (number not included).
  • Closed Circle: Used for ≤ and ≥ (number included).

Compound Inequalities

  • Compound inequalities involve two inequality symbols and define a range between two values.

certified Physics and Maths tutor

 

 

Solved Example 5: 

Question: 1 < x ≤ 5

Solution: 

Interpretation:

  • x is greater than 1 but less than or equal to 5.

Steps to Plot:

Step 1: Draw a number line and label points 1 and 5.

Number line with labeled points 1 through 7

Step 2: Place an open circle at 1 (since x is not equal to 1).

Number line with an open circle at 1, indicating that 1 is not included in the solution. Title: Number Line with Open Circle at Point 1

Step 3: Place a closed circle at 5 (since x can be equal to 5).

Number line with an open circle at 1 and a closed circle at 5, indicating the range of values from 1 to 5.

Step 4: Shade the region between 1 and 5, connecting the two circles.

Number line with an open circle at 1 and a closed circle at 5, with a shaded region between the two points.

certified Physics and Maths tutor

 

 

Solved Example 6: 

Question: −2 ≤ x < 3

Solution: 

Interpretation:

  • x is greater than or equal to -2 but less than 3.

Steps to Plot:

Step 1: Draw a number line and mark -2 and 3.

Number line with points marked at -2 and 3.

Step 2: Place a closed circle at -2 (including -2 in the solution)

Number line with a closed circle at -2.

Step 3: Place an open circle at 3 (excluding 3)

Number line with an open circle at 3.

Step 4: Shade the region between -2 and 3.

Number line shaded between -2 and 3 with a closed circle at -2 and an open circle at 3.

Important Notes on Inequality Direction

  • Direction Matters: The inequality symbol points towards the smaller value
  • Equivalent Expressions:
    • x>2 is the same as 2<x
    • Both indicate that x is greater than 2.

Example:

  • 2<x Reads as “2 is less than x,” meaning x is greater than 2.
  • x>2: Reads as “x is greater than 2.”

Understanding this helps avoid confusion when interpreting or rearranging inequalities.

Practice Problems

Try plotting the following inequalities on a number line:

1. x ≥ −4

Inequality x ≥ -4, indicating that x can be -4 or any number greater than -4.

    • Interpretation: x is -4 or any number greater.
    • Plot: Closed circle at -4, shade to the right.

A number line representing x ≥ -4 with a closed circle at -4 and shading to the right. Title: Graphical Representation of x ≥ -4

 

2. x < 0

Inequality x < 0, indicating that x is any number less than 0.

    • Interpretation: x is any number less than 0.
    • Plot: Open circle at 0, shade to the left.

Number line showing x less than 0, with an open circle at 0 and shading to the left representing all values less than 0.

3. −3 < x ≤ 2 

Inequality −3 < x ≤ 2 showing x is between −3 and 2, including 2

    • Interpretation: x is greater than -3 and up to 2, including 2.
    • Plot: Open circle at -3, closed circle at 2, shade between them.

Number line showing the inequality −3 < x ≤ 2, with an open circle at -3 and a closed circle at 2. The shaded region between the circles represents all values of x between −3 and 2, including 2 but excluding −3.

Conclusion

Understanding how to solve inequalities and represent them on a number line is a crucial skill in algebra. Remember:

  • Use open circles for < and > (number not included).
  • Use closed circles for ≤ and ≥ (number included).
  • Shade appropriately to represent all possible values of x that satisfy the inequality.
  • Pay attention to the direction of the inequality symbol.

Practice Questions and Answers on Inequalities on a Number Line

Question 1: Represent the inequality x < 4 on a number line.

Question 2: Sketch the inequality x ≥ −3 on a number line.

Question 3: Plot the inequality x > 0 on a number line.

Question 4: Illustrate the inequality x ≤ 6 on a number line.

Question 5: Show the solution of the compound inequality −2 < x ≤ 5 on a number line.

Question 6: Represent the inequality x ≥ −7 on a number line.

Question 7: Graph the inequality x ≤ 2 on a number line.

Question 8: Plot the compound inequality 1 ≤ x < 4 on a number line.

Question 9:Illustrate the inequality x > −5 on a number line.

Question 10: Show the solution set for the compound inequality −3 ≤ x ≤ 3 on a number line.

Solutions

Question 1: 

Number line representing the inequality x < 4 with an open circle at 4 and shading to the left.

Step 1: Draw a Horizontal Number Line:

  • Sketch a straight horizontal line.
  • Mark evenly spaced intervals.

Step 2: Mark the Key Point (4):

  • Locate and label the point corresponding to x = 4 on the number line.

Step 3: Place an Open Circle at 4:

  • Draw an open (hollow) circle at the point labelled 4.
  • Reason: The inequality is “less than” (<), so 4 is not included in the solution set.

Step 4: Shade to the Left of 4:

  • Draw a line or arrow extending from the open circle to the left.
  • Reason: To represent all real numbers less than 4.

 

Question 2:

Number line representing the inequality x ≥ -3 with a closed circle at -3 and shading to the right.

Step 1: Draw a Horizontal Number Line:

  • Sketch a straight horizontal line with intervals.

Step 2: Mark the Key Point (-3):

  • Locate and label the point corresponding to x = −3.

Step 3: Place a Closed Circle at -3:

  • Draw a closed (filled-in) circle at -3.
  • Reason: The inequality is “greater than or equal to” (≥), so -3 is included in the solution set.

Step 4: Shade to the Right of -3:

  • Draw a line or arrow extending from the closed circle to the right.
  • Reason: To represent all real numbers greater than or equal to -3.

Question 3:

Number line representing the inequality x > 0 with an open circle at 0 and shading to the right.

Step 1: Draw a Horizontal Number Line:

  • Sketch the number line with appropriate intervals.

Step 2: Mark the Key Point (0):

  • Locate and label the point x = 0.

Step 3: Place an Open Circle at 0:

  • Draw an open circle at 0.
  • Reason: The inequality is “greater than” (>), so 0 is not included.

Step 4: Shade to the Right of 0:

  • Extend a line or arrow from the open circle to the right.
  • Reason: To represent all real numbers greater than 0.

 

Question 4:

Number line representing the inequality x ≤ 6 with a closed circle at 6 and shading to the left.

Step 1: Draw a Horizontal Number Line.

Step 2: Mark the Key Point (6):

  • Locate and label x = 6.

Step 3: Place a Closed Circle at 6:

  • Draw a closed circle at 6.
  • Reason: The inequality is “less than or equal to” (≤), so 6 is included.

Step 4: Shade to the Left of 6:

  • Draw a line or arrow extending left from the closed circle.
  • Reason: To represent all real numbers less than or equal to 6.

 

Question 5:

Number line representing the inequality -2 < x ≤ 5 with an open circle at -2 and a closed circle at 5, shading between them.

Step 1: Draw a Horizontal Number Line.

Step 2: Mark the Key Points (-2 and 5):

  • Label x = −2 and x = 5.

Step 3: Place an Open Circle at -2:

  • Draw an open circle at -2.
  • Reason: The inequality is “greater than” (>), so -2 is not included.

Step 4: Place a Closed Circle at 5:

  • Draw a closed circle at 5.
  • Reason: The inequality is “less than or equal to” (≤), so 5 is included.

Step 5: Shade the Region Between -2 and 5:

  • Draw a line connecting the two circles.
  • Reason: To represent all real numbers greater than -2 and less than or equal to 5.

Question 6:

Number line representing the inequality x ≥ -7 with a closed circle at -7 and shading to the right.

Step 1: Draw a Horizontal Number Line.

Step 2: Mark the Key Point (-7):

  • Label x = −7.

Step 3: Place a Closed Circle at -7:

  • Draw a closed circle at -7.
  • Reason: The inequality is “greater than or equal to” (≥), so -7 is included.

Step 4: Shade to the Right of -7:

  • Extend a line or arrow from the closed circle to the right.
  • Reason: To represent all real numbers greater than or equal to -7.

 

Question 7:

Number line representing the inequality x ≤ 2 with a closed circle at 2 and shading to the left.

Step 1: Draw a Horizontal Number Line.

Step 2: Mark the Key Point (2):

  • Label x = 2.

Step 3: Place a Closed Circle at 2:

  • Draw a closed circle at 2.
  • Reason: The inequality is “less than or equal to” (≤), so 2 is included.

Step 4: Shade to the Left of 2:

  • Draw a line or arrow extending left from the closed circle.
  • Reason: To represent all real numbers less than or equal to 2.

 

Question 8:

Number line representing the inequality 1 ≤ x < 4 with a closed circle at 1 and an open circle at 4, shading between them.

Step 1: Draw a Horizontal Number Line.

Step 2: Mark the Key Points (1 and 4):

  • Label x = 1 and x = 4.

Step 3: Place a Closed Circle at 1:

  • Draw a closed circle at 1.
  • Reason: The inequality is “greater than or equal to” (≥), so 1 is included.

Step 4: Place an Open Circle at 4:

  • Draw an open circle at 4.
  • Reason: The inequality is “less than” (<), so 4 is not included.

Step 5: Shade the Region Between 1 and 4:

  • Draw a line connecting the two circles.
  • Reason: To represent all real numbers from 1 up to (but not including) 4.

 

Question 9:

Number line representing the inequality x > -5 with an open circle at -5 and shading to the right.

Step 1: Draw a Horizontal Number Line.

Step 2: Mark the Key Point (-5):

  • Label x = −5.

Step 3: Place an Open Circle at -5:

  • Draw an open circle at -5.
  • Reason: The inequality is “greater than” ( > >), so -5 is not included.

Step 4: Shade to the Right of -5:

  • Extend a line or arrow from the open circle to the right.
  • Reason: To represent all real numbers greater than -5.

 

Question 10:

Number line representing the inequality -3 ≤ x ≤ 3 with closed circles at -3 and 3 and shading between them.

Step 1: Draw a Horizontal Number Line.

Step 2: Mark the Key Points (-3 and 3):

  • Label x = −3 and x = 3.

Step 3: Place a Closed Circle at -3:

  • Draw a closed circle at -3.
  • Reason: The inequality is “greater than or equal to” (≥), so -3 is included.

Step 4: Place a Closed Circle at 3:

  • Draw a closed circle at 3.
  • Reason: The inequality is “less than or equal to” ( ≤ ≤), so 3 is included.

Step 5: Shade the Region Between -3 and 3:

  • Draw a line connecting the two closed circles.
  • Reason: To represent all real numbers between -3 and 3, including both endpoints.

Table of Content

Join Tutoring