Histogram Graph Questions and, Examples with Worksheet

Calculator
Test Yourself

Histogram

  • Histograms are an important tool for visualizing data in a graphical format.
  • A histogram is a type of graph that displays the frequency distribution of a dataset.
  • It is commonly used in statistics and data analysis to summarize and interpret large amounts of information.

In this article, we will discuss: 

  1. What is a Histogram?
  2. We will explore the key features of histograms, their differences from bar charts, and how to draw and interpret them effectively.

Here is one more link to practice a few extra questions: Maths Genie Histogram Questions

Request for Demo Lesson

What is a Histogram?

  • A histogram is a type of graph that displays the frequency distribution of a dataset.
  • It represents data using a series of bars, where each bar represents a specific range of values called a bin.
  • The height of each bar corresponds to the frequency of data points that fall within that bin.

Histogram frequency distribution graph

Histograms vs Bar Charts

  • Histograms are often confused with bar charts, but they are not the same thing.
  • While both graphs use bars to represent data, the key difference is in the type of data they represent.
  • Bar charts are used to compare data across different categories, while histograms are used to display frequency distributions of continuous data.
  • In other words, bar charts are used for qualitative data, while histograms are used for quantitative data.
Histograms vs Bar Charts and what is a histogram

What is Frequency Density?

  • Frequency density is a way of measuring the frequency of data in a histogram.
  • It is calculated by dividing the frequency of each bin by the width of the bin.
  • This gives the frequency density of the data within each bin, allowing us to compare the distribution of data across different bins.

Frequency density = frequency/width of bin

How to find Frequency Density for Histograms

  • To find the frequency density for a histogram, you need to divide the frequency of each bin by the width of the bin.
  • The width of each bin is the range of values that it covers. For example, if a bin covers values from 20 to 30, its width would be 10.
  • To calculate the frequency density for this bin, you would divide its frequency by 10.

certified Physics and Maths tutor

 

 

Solved Example: 

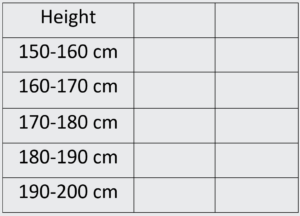
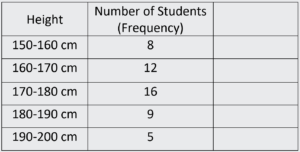
Question 1: Suppose we have collected data on the heights of 50 students in a class, and we want to create a histogram to represent this data. We group the heights into bins, with each bin representing a range of heights. Let’s say we have five bins with the following ranges:

Frequency Example

Solution: 

We then count the number of students whose height falls within each bin.

Let’s say we get the following frequencies:

  • 8 students in the 150-160 cm bin
  • 12 students in the 160-170 cm bin
  • 16 students in the 170-180 cm bin
  • 9 students in the 180-190 cm bin
  • 5 students in the 190-200 cm bin

Frequency Example Table 2

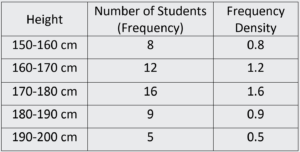
To calculate the frequency density for each bin, we use the formula:

Frequency density = frequency/width of bin

For example, for the first bin, the width is 10 cm, so the frequency density is:

Frequency density for 150-160 cm

bin = 8 / 10

= 0.8

Similarly, we can calculate the frequency density for each bin:

• Frequency density for 150-160 cm bin = 0.8
• Frequency density for 160-170 cm bin = 1.2
• Frequency density for 170-180 cm bin = 1.6
• Frequency density for 180-190 cm bin = 0.9
• Frequency density for 190-200 cm bin = 0.5

Frequency Example Table 3

By using frequency density instead of frequency, we can compare the distribution of data across bins with different widths.

In this example, we can see that the distribution is highest in the 170-180 cm bin, which has the highest frequency density of 1.6.

Steps to draw a Histogram

To draw a histogram, follow these steps:

  • Step #1: Determine the range of the data and divide it into equal-sized bins.
  • Step #2: Count the number of data points that fall within each bin.
  • Step #3: Calculate the frequency density for each bin.
  • Step #4: Draw the x-axis with the range of the data and the y-axis with the frequency density.
  • Step #5: Draw a rectangle for each bin with a height corresponding to its frequency density.

certified Physics and Maths tutor

 

 

Solved Example

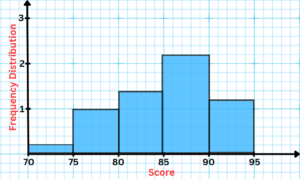
Question: Let’s say we have the following data set representing the scores of 30 students in a math test: 80, 78, 90, 85, 92, 84, 77, 85, 88, 80, 75, 72, 85, 90, 88, 92, 78, 82, 86, 90, 82, 83, 85, 88, 92, 89, 86, 80, 78, 85. We aim to construct a histogram to visually represent the score distribution. Here’s how we can do it:

Solution: 

  • Step #1: Determine the range of the data and divide it into equal-sized bins.

    The range of the data is 20 (92-72).

    We can divide it into 5 bins of size 5:

Histogram Solved Example Table

  • Step #2: Count the number of data points that fall within each bin.

    Using the bins, we created in step #1,

    we can count the number of scores that fall within each bin:

Frequency Distribution table

  • Step #3: Calculate the frequency density for each bin.

    To calculate the frequency density for each bin,

    we divide the frequency (number of scores) by the width of the bin (4):

    70-74: 1/5 = 0.2

    75-79: 5/5 = 1 

    80-84: 7/5 = 1.4

    85-89: 11/5 = 2.2

    90-94: 6/5 = 1.2  

Frequency Distribution

  • Step #4: Draw the x-axis with the range of the data and the y-axis with the frequency density. We draw the x-axis with the bins we created in step #1 and the y-axis with the frequency

    Histogram Graph

Steps to Interpret data from Histogram

  • When interpreting histograms, it is important to note that the frequency density (y-) axis does not directly tell us the frequency.
  • Instead, the frequency is proportional to the area of the bar.

To find the frequency for each bin, you can use the formula frequency equals area.

The formula frequency equals area.

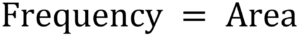
  • This means that the frequency is equal to the area of the bar, which can be determined by finding the product of the width and height of the bar.
  • However, there may be cases where the frequency is only proportional to the area of the bar, in which case you would need to use the formula frequency equals k cross times area.

The formula frequency equals k x area

  • Here, k is a constant that needs to be determined from other information given in the question.
  • If you need to estimate the frequency of a part of a bar or class interval within a histogram, you can find the area of the relevant part of the bar and then use the formula mentioned above to find the frequency

certified Physics and Maths tutor

 

 

Solved Example

Question: The table below and its corresponding histogram show the mass, in kg, of some newborn bottlenose dolphins.

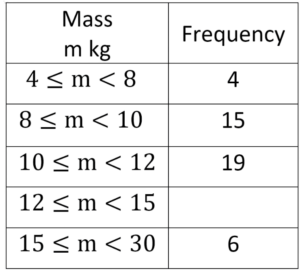
Histogram Question Table

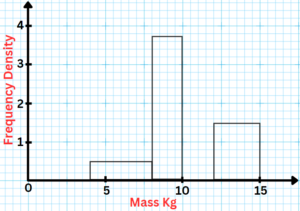
Histogram mass kg

(a) Use the table and histogram to find the value of k in the formula

(b) Estimate the number of dolphins whose weight is greater than 13 kg.

Solution: 

(a) 

Histogram frequency density Formula

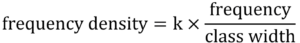
Start by finding the frequency density in terms of k – add two columns to the table, one for class width, one for frequency density

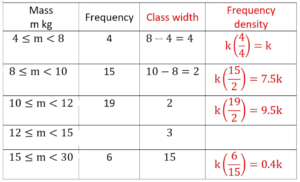
Finding the frequency density Table

We can use either of the two intervals that feature both in the table and on the histogram to find the value of k

Using the first bar

Check using the other (2nd) bar to check: 7.5k = 3.75, k = 0.5

(b) Estimate the number of dolphins whose weight is greater than 13 kg.

Solution:

We can see from the table that there are 6 dolphins in the interval 15 ≤ m <30.

So we need to estimate the number of dolphins that are in the interval 13≤ m <15.

For 13≤ m <15, the histogram shows the frequency density is 1.5 and we found the value of k in part(a).

Using the formula given in the question

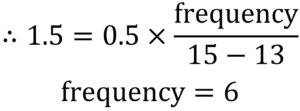
Histogram frequency density Answer

So the total number of can be estimated by

6 + 6 = 12

There are approximately 12 dolphins with a weight greater than 13kg