Fractional Indices | GCSE Maths

In this lesson, we will discuss what Fractional Indices are, how they are simplified, and the logic behind negative fractional indices. We will also walk through step-by-step examples to help you understand the concepts and solve some GCSE Past Paper Questions

What Are Indices?

Indices (also known as exponents) allow us to write repeated multiplication in a simpler way. For example:

x² means “x multiplied by itself” , or “x times x”.
x³ means “x multiplied by itself three times” , or x times x times x.
In general, “xⁿ means you multiply x by itself n times”.

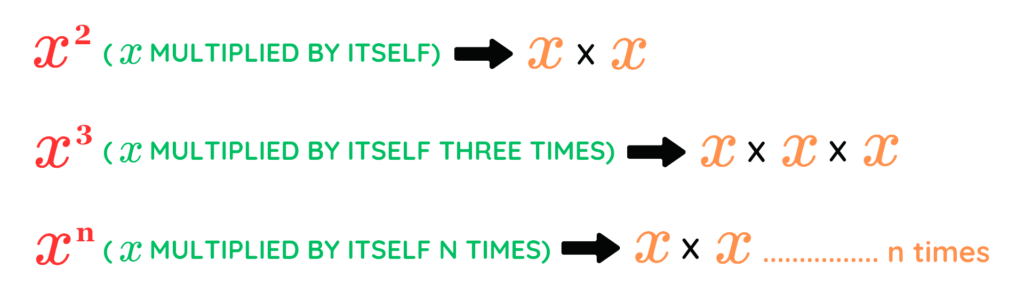
$Illustration of fractional indices with examples of x², x³, and xⁿ in mathematics.$

This idea is fundamental to working with more advanced topics like fractional indices.

What Are Fractional Indices?

Fractional indices are Exponents written as fractions, for example,

x^m/n

They combine the ideas of Powers and Roots into a single operation:

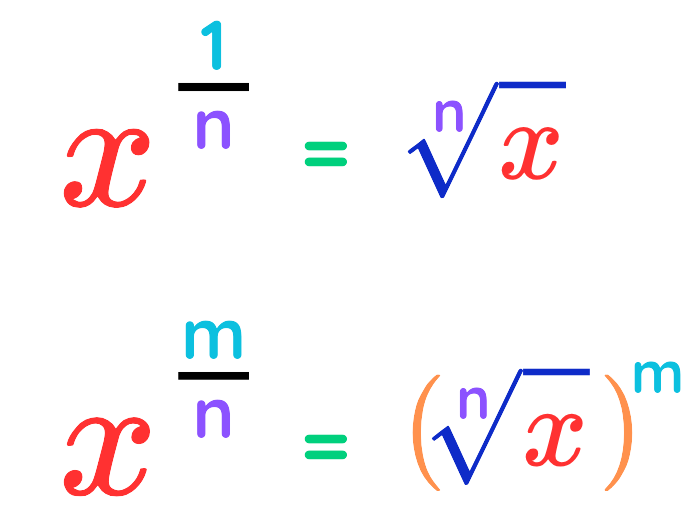
$Mathematical representation of fractional indices, showing the conversion of exponents into roots.$

This means you take the n-th root of x first, then raise the result to the power of m.

Which is the same as raising the n-th root of x to the power m

Numerator (m): Indicates the power (How many times x is multiplied by itself).
Denominator (n): Indicates the root (Which root to take of x).

Some examples of fractional exponents that are widely used are given below:

Steps for Simplifying Fractional Indices

Step #1: Identify the Fractional Exponent

If you see x^m/n, recognize that:
- m is the power.
- n is the root (i.e., the n-th root).

Step #2: Rewrite in Root Form

Convert

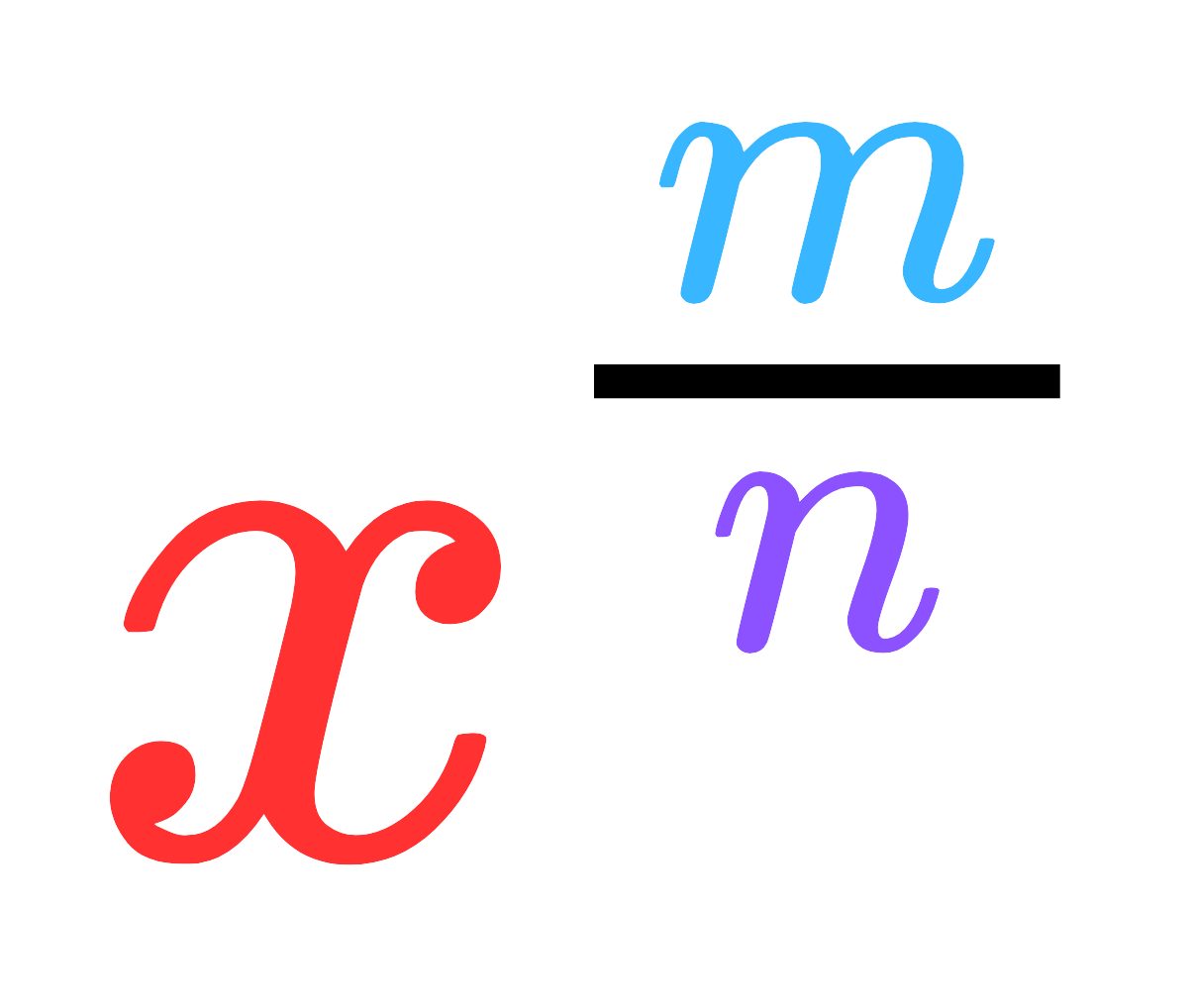
into

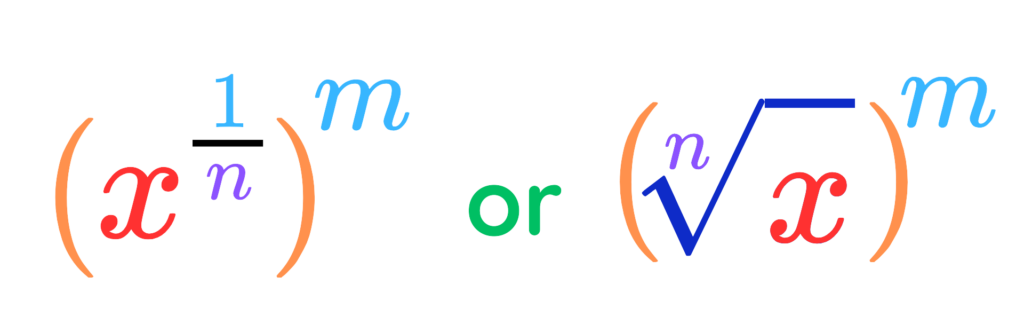
Step #3: Find the n-th Root

If the number is a perfect power, you might see the root immediately (e.g., ∛27 = 3).
If you’re not sure, use prime factorization.

Step #4: Apply the Power

After finding the n-th root, raise it to the power m.

Step #5: Combine and Simplify

Simplify any remaining exponents or multiply out any obvious powers.

Solved Example 1

Problem: Simplify:

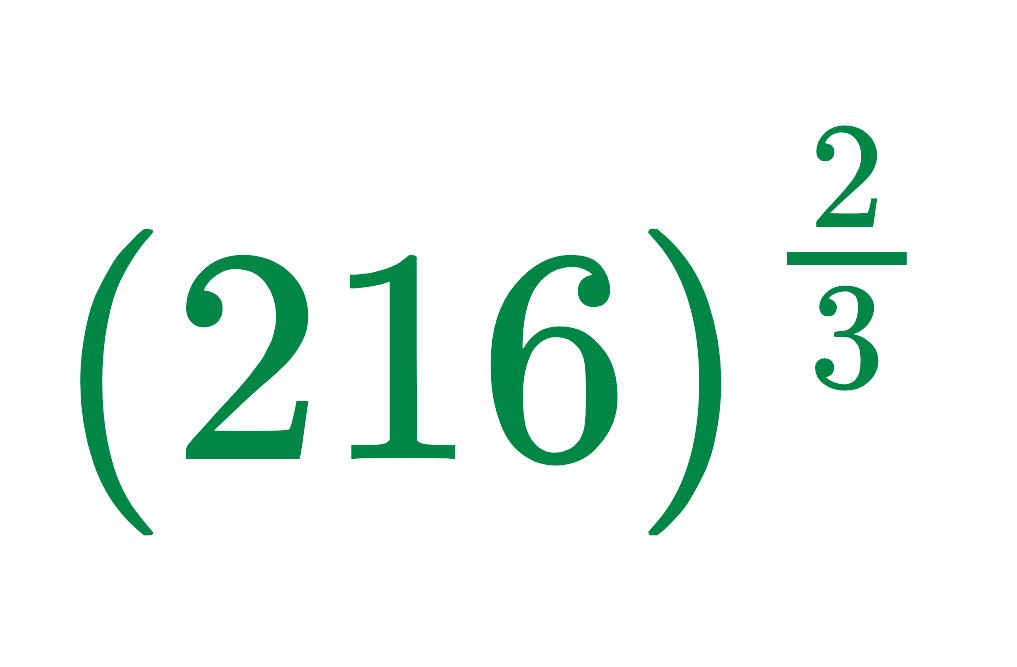
$Mathematical representation of 216^(2/3) as a fractional exponent$

Solution:

Step #1: Identify the Exponent

2/3 means power = 2 and root = 3

Step #2: Rewrite as a Root First

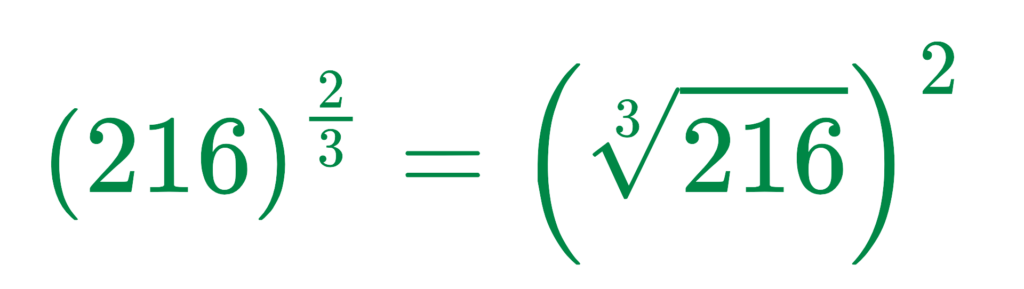
Step #3: Find the Cube Root 216^1/3

- Prime-factorize 216:

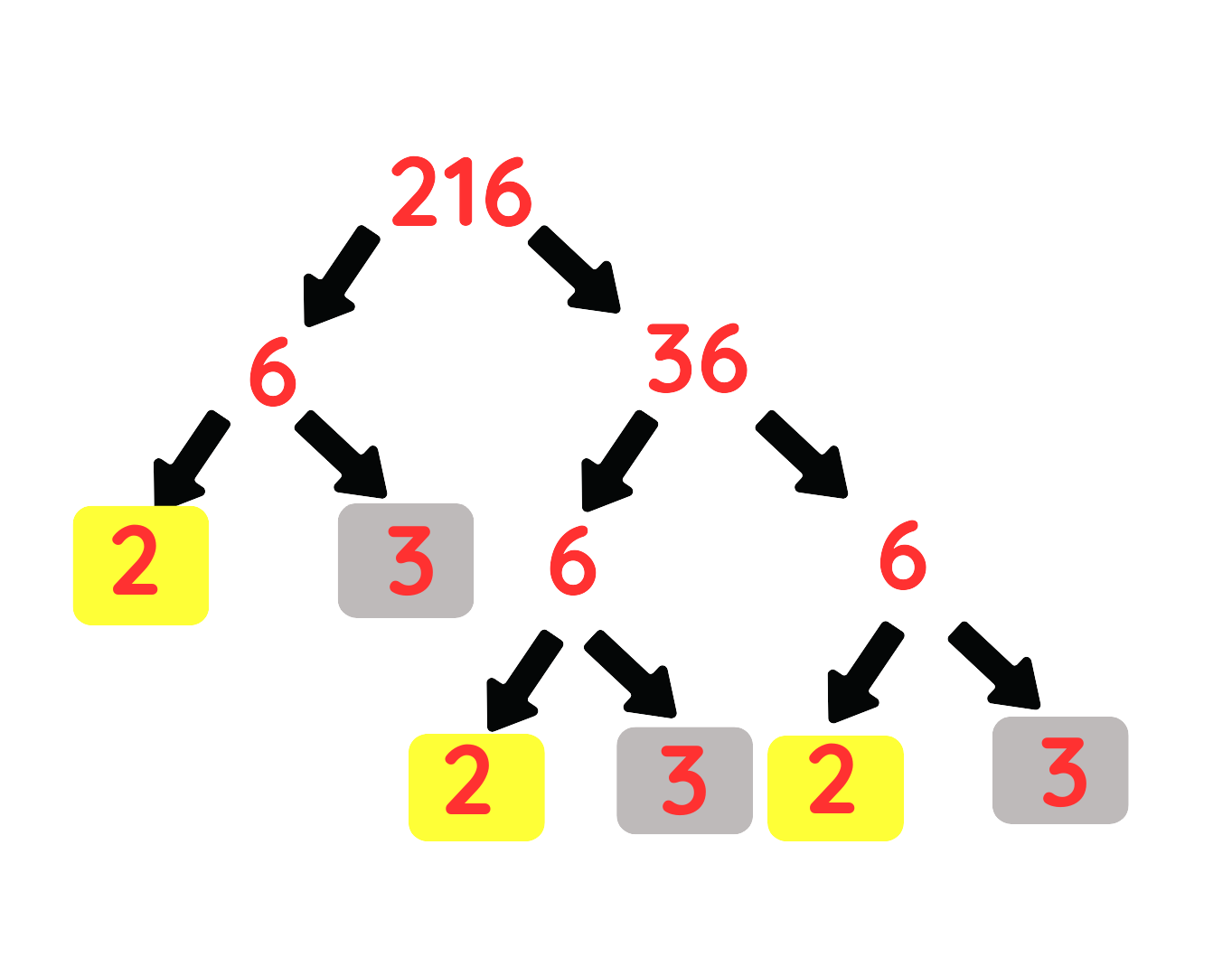
216 = 2³ × 3³

so,

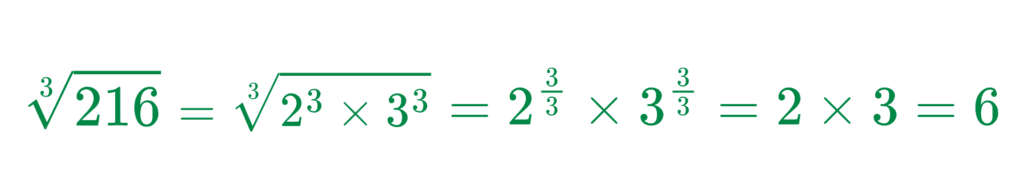
Step #4: Apply the Power m = 2

(6)² = 36

Step #5: Final Answer

216^2/3 = 36

Using these clear steps—and prime factorization when you’re unsure about the root—makes fractional indices much easier to handle.

In the previous example, 216 was a perfect cube—making it straightforward to take the cube root.
However, not all numbers factor into perfect powers so neatly.

Let’s look at another example with 250, which will result in a simplified radical rather than a whole number.

Solved Example 2

Problem: Simplify:

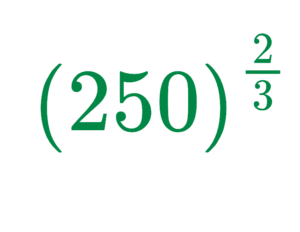
$Mathematical representation of 250^(2/3) as a fractional exponent$

Solution:

Step #1: Identify the Exponent

2/3 means power = 2 and root = 3

Step #2: Rewrite in Root Form

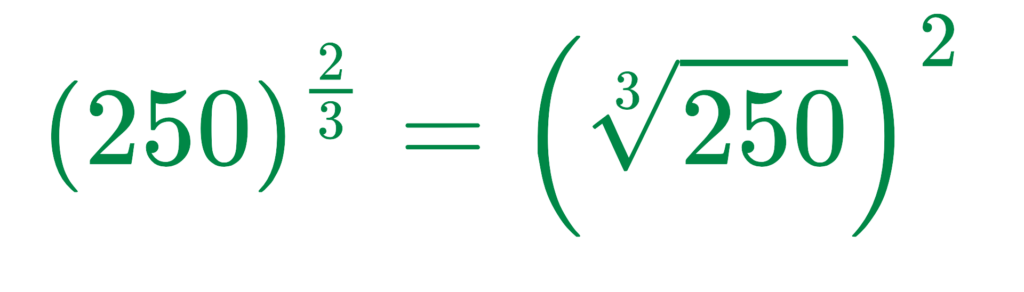
Step #3: Prime-Factorize 250

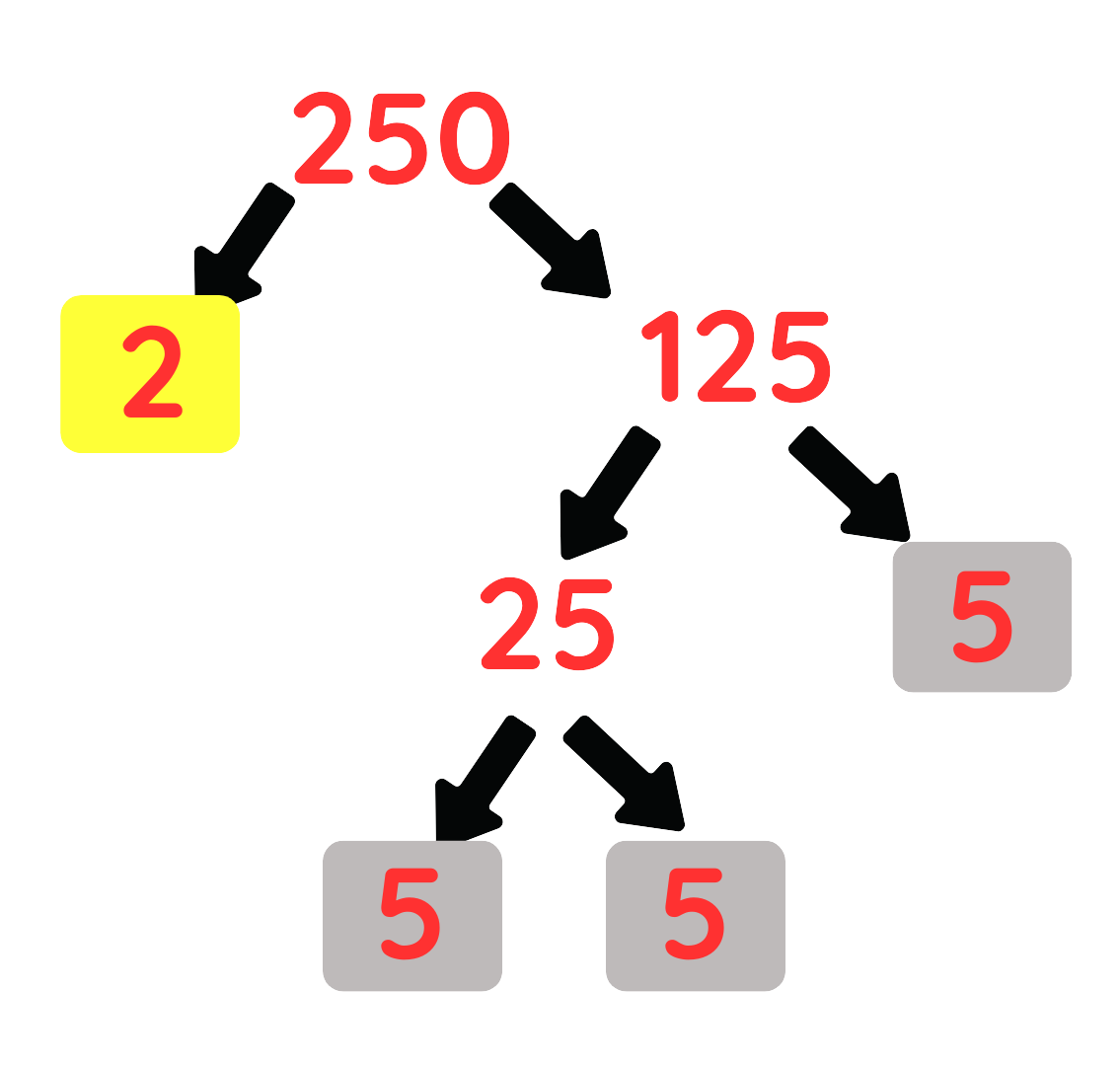
250 = 2 × 125 = 2 × 5³

so,

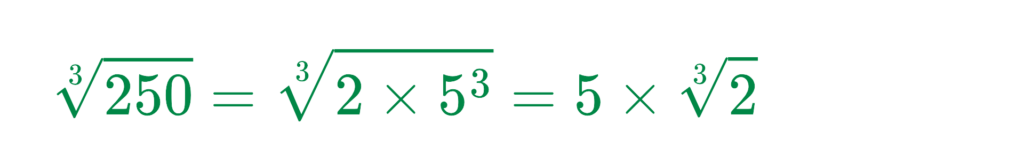
Step #4: Apply the Power m = 2

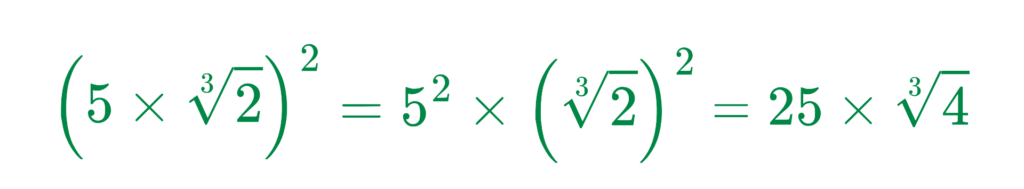
Step #5: Final Answer

(250)^2/3 = 25 ∛4

If you prefer a decimal approximation, then ∛4 ≈ 1.5874

so,

25 × 1.5874 ≈ 39.685

Video Tutorial on Fractional Indices

Watch this Video Tutorial as we explain step by step to Find Fractional Indices.

Practice Questions and Answers on Fractional Indices

Question 1: Simplify: 125^2/3

Question 2: Simplify: 64^3/2

Question 3: Simplify: 500^2/3

Question 4:Simplify: 32^4/5

Question 5: Simplify: 81^3/4

Question 6: Simplify: 729^2/3

Question 7: Simplify: 128^3/7

Question 8: Simplify: 1000^2/3

Question 9: Simplify: 16^5/4

Question 10: Simplify: 243^4/5

Solutions

Question 1:

Solution:

Step #1: Identify the Exponent

The exponent 2/3 means the power is 2 and the root is 3.

Step #2: Rewrite in Root Form

125^2/3 = (125^1/3)²

Step #3: Prime-Factorize 125

125 = 5³
∛125 is 5.

Step #4: Apply the Power (2)

5² = 25

Step #5: Final Result

125^2/3 = 25

Question 2:

Solution:

Step #1: Identify the Exponent

The exponent 3/2 means the power is 3 and the root is 2.

Step #2: Rewrite in Root Form

64^3/2 = (64^1/2)³

Step #3: Prime-Factorize 64

√64 is 8.

Step #4: Apply the Power (3)

8³ = 512

Step #5: Final Result

64^3/2 = 512

Question 3:

Solution:

Step #1: Identify the Exponent

The exponent 2/3 means the power is 2 and the root is 3.

Step #2: Rewrite in Root Form

500^2/3 = (500^1/3)²

Step #3: Prime-Factorize 500

500 = 2 × 5³
∛500 is 5 × ∛2.

Step #4: Apply the Power (2)

(5 × ∛2)² = 25 × ∛4

Step #5: Final Result

500^2/3 = 25 × ∛4

Question 4:

Solution:

Step #1: Identify the Exponent

The exponent 4/5 means the power is 4 and the root is 5.

Step #2: Rewrite in Root Form

32^4/5 = (32^1/5)⁴

Step #3: Fifth Root of 32

Fifth root of 32 is 2.

Step #4: Apply the Power (4)

2⁴ = 16

Step #5: Final Result

32^4/5 = 16

Question 5:

Solution:

Step #1: Identify the Exponent

The exponent 3/4 means the power is 3 and the root is 4.

Step #2: Rewrite in Root Form

81^3/4 = (81^1/4)³

Step #3: Fourth Root of 81

Fourth root of 81 is 3.

Step #4: Apply the Power (3)

3³ = 27

Step #5: Final Result

81^3/4 = 27

Question 6:

Solution:

Step #1: Identify the Exponent

The exponent 2/3 means the power is 2 and the root is 3.

Step #2: Rewrite in Root Form

729^2/3 = (729^1/3)²

Step #3: ∛729

∛729 is 9

Step #4: Apply the Power (2)

9² = 81

Step #5: Final Result

729^2/3 = 81

Question 7:

Solution:

Step #1: Identify the Exponent

The exponent 3/7 means the power is 3 and the root is 7.

Step #2: Rewrite in Root Form

128^3/7 = (128^1/7)³

Step #3: Seventh Root of 128

Seventh root of 128 is 2.

Step #4: Apply the Power (3)

2³ = 8

Step #5: Final Result

128^3/7 = 8

Question 8:

Solution:

Step #1: Identify the Exponent

The exponent 2/3 means the power is 2 and the root is 3.

Step #2: Rewrite in Root Form

1000^2/3 = (1000^1/3)²

Step #3: Cube Root of 1000

Cube root of 1000 is 10.

Step #4: Apply the Power (2)

10² = 100

Step #5: Final Result

1000^2/3= 100

Question 9:

Solution:

Step #1: Identify the Exponent

The exponent 5/4 means the power is 5 and the root is 4.

Step #2: Rewrite in Root Form

16^5/4 = (16^1/4)⁵

Step #3: Fourth Root of 16

Fourth root of 16 is 2.

Step #4: Apply the Power (5)

2⁵ = 32

Step #5: Final Result

16^5/4= 32

Question 10:

Solution:

Step #1: Identify the Exponent

The exponent 4/5 means the power is 4 and the root is 5.

Step #2: Rewrite in Root Form

243^4/5 = (243^1/5)⁴

Step #3: F Fifth Root of 243

Fifth root of 243 is 3.

Step #4: Apply the Power (4)

3⁴ = 81

Step #5: Final Result

243^4/5= 81

Table of Content

Video Tutorial on Fractional Indices
What are indices?
What Are Fractional Indices?
Steps for Simplifying Fractional Indices
Solved Examples