Enlargement Using a Negative Scale Factor | GCSE Maths

Practice Questions
Downloads

Video Tutorial on Enlargement Using a Negative Scale Factor

  • Watch this Video Tutorial as we explain step by step to Find Enlargement Using a Negative Scale Factor

What is Enlargement?

  • Enlargement is when we change the size of a shape while keeping its proportions intact.
  • You can think of it like zooming in or out on your smartphone—the shape gets bigger or smaller,

Animated explanation of enlargement in GCSE Maths, showing how a shape changes size while maintaining its proportions, including an example with a negative scale factor.

but the overall shape stays the same without getting stretched or squished.

  • If the scale factor is greater than 1, the shape gets larger (magnified).
    For example, let’s say you have a right triangle with a base of 3 cm and a height of 4 cm. If the scale factor is 2, all dimensions are doubled.

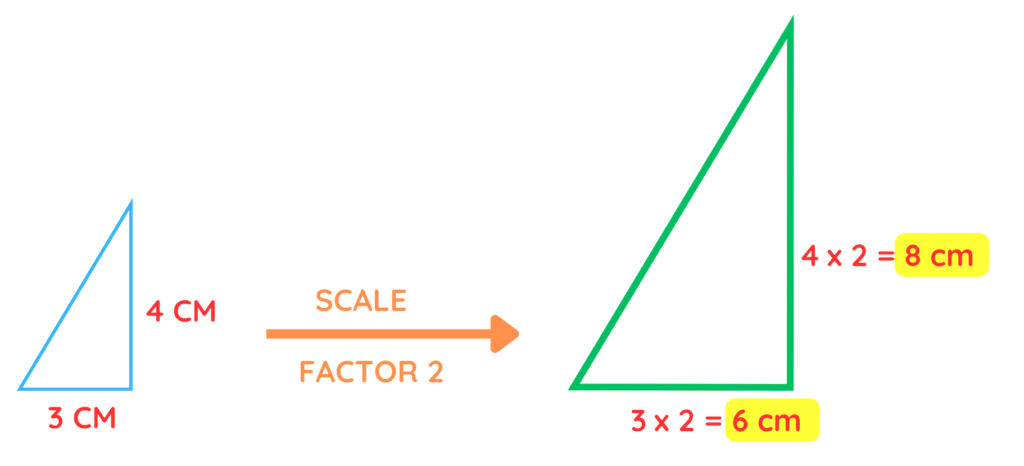
Example of enlargement using a scale factor of 2, illustrating the concept of enlargement and setting the foundation for understanding negative scale factors.

The new triangle will have a base of 6 cm and a height of 8 cm.

  • If the scale factor is between 0 and 1, the shape gets smaller.
    For example, take the same right triangle with a base of 3 cm and a height of 4 cm. If the scale factor is 1/2, all dimensions are halved.

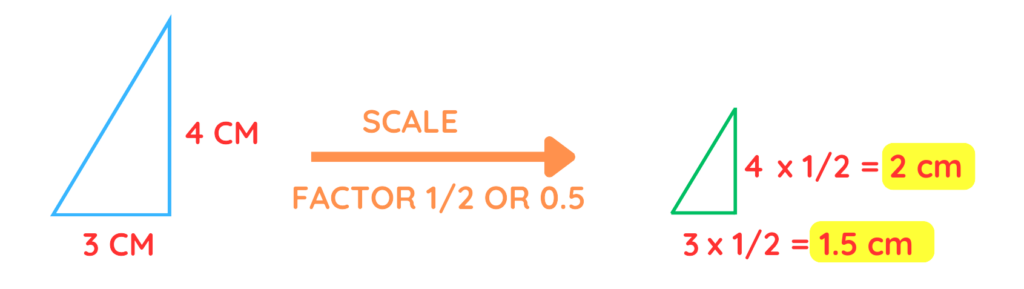
Example of enlargement with a scale factor of 1/2, showing how a right triangle is reduced in size to half its dimensions, illustrating the foundation of negative scale factors.

The new triangle will have a base of 1.5 cm and a height of 2 cm.

Centre of Enlargement

  • The centre of enlargement is the point about which all the transformations of the shape takes place. This point is generally given in the question.
  • It is a fixed point from which all measurements are taken and scaled.
  • This point plays a crucial role in determining how the shape is transformed.

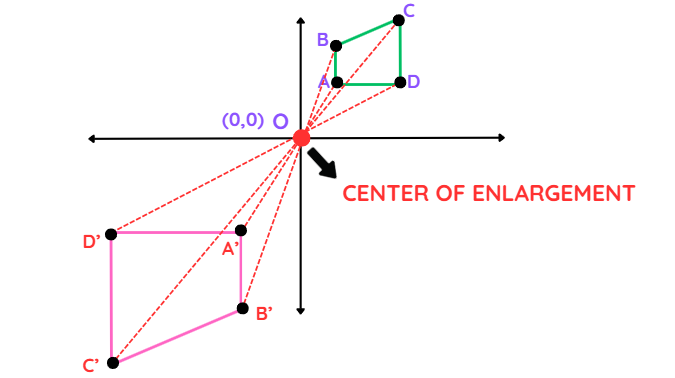
In this image, the shape has been enlarged with a centre of enlargement (shown as O) at the origin.

What Are Negative Scale Factors?

Negative scale factor produces an image on the opposite side of the centre of enlargement and it is also flips the shape upside down.

  • The shape moves to the opposite side of the centre of enlargement.

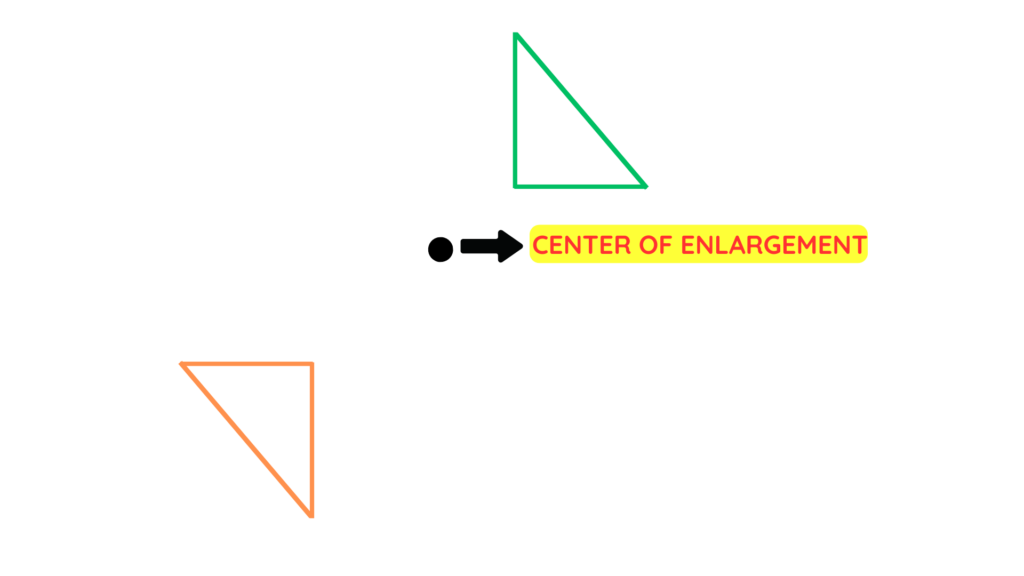
  • It’s flipped, like a mirror image.

  • The size changes based on the scale factor’s absolute value (ignoring the negative sign in front of it).

Steps to Find Enlargement Using a Negative Scale Factor (Integer Scale Factor)

certified Physics and Maths tutor

 

 

Solved Example 1

Question: For the figure given below, find the enlargement of the object with a scale factor of -2 about the centre of enlargement at the origin.

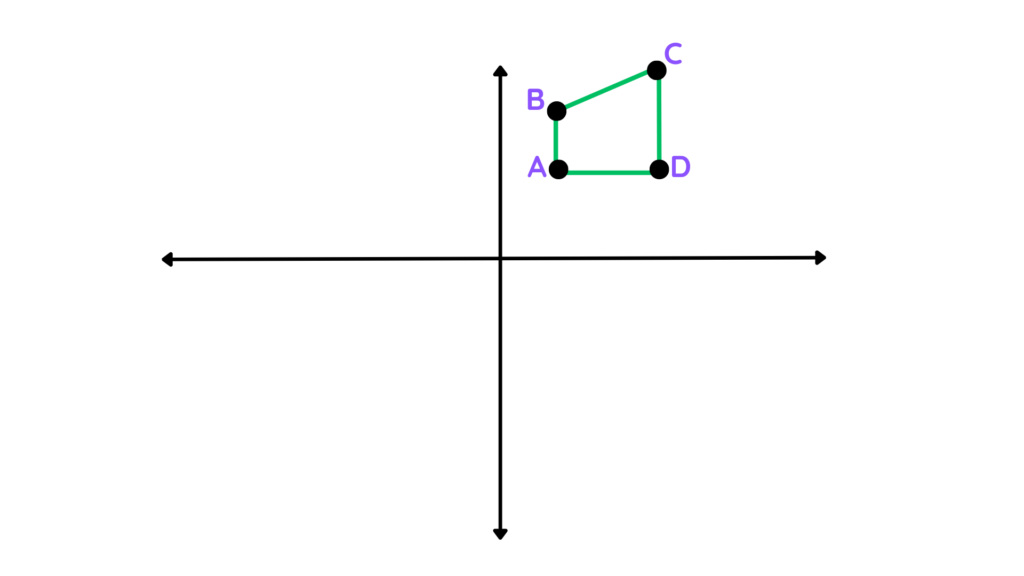
Solution: 

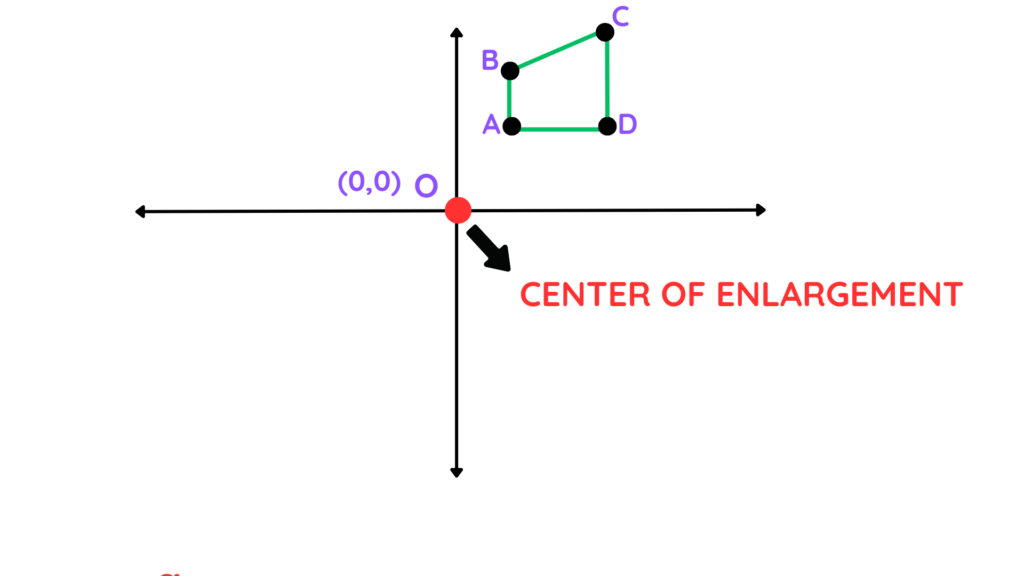
Step 1: Mark the centre of enlargement:

  • The centre of enlargement is the point about which all the transformations of the shape takes place. This point is generally given in the question. In our example, we are given the origin as the centre of enlargement.

Diagram showing how to mark the center of enlargement, positioned at the origin, for transformations involving negative scale factors

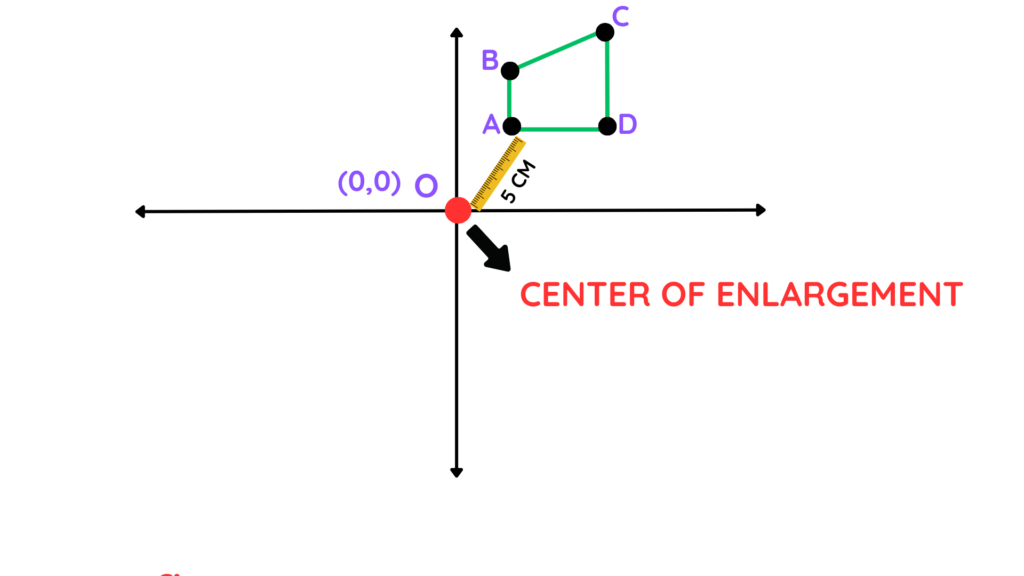
Step 2: Take a ruler and measure the distance from the centre of enlargement to one vertex of the shape.

  • Choose any one vertex of your shape, and measure the distance between this vertex and the origin. Let’s use a point A.
  • Suppose the distance OA comes out to be 5 cm.

Diagram showing how to measure the distance from the center of enlargement to a vertex for transformations using negative scale factors.

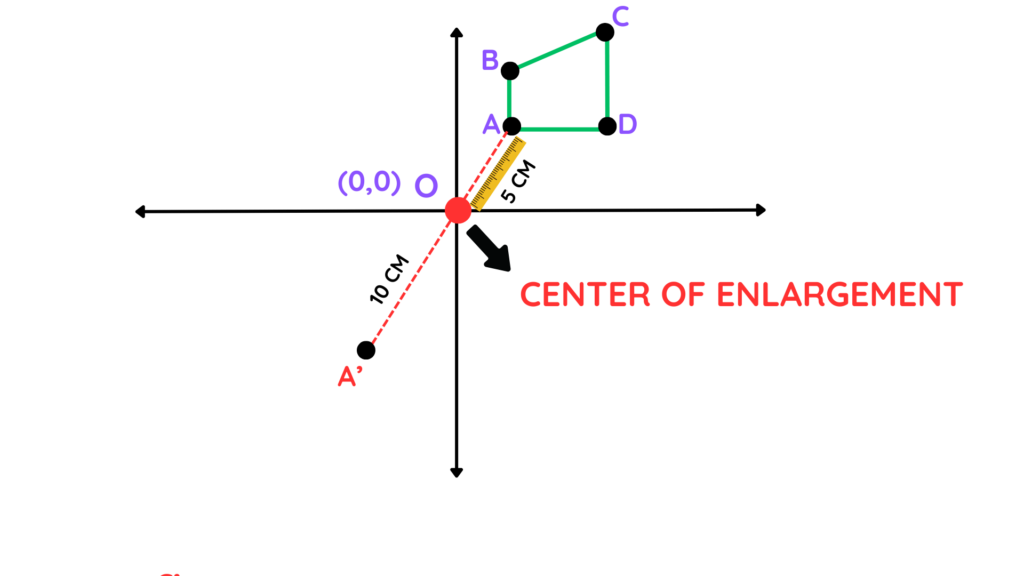
Step 3: Multiply by the scale factor:

  • For now, ignore the minus sign.
  • Multiply 5 cm by 2

5 × 2 = 10 cm

Step 4: Extend the line:

  • Extend the line OA by 10 cm TO THE OTHER SIDE  of the origin and mark the point A′ there.

Diagram showing how to extend the line from the center of enlargement through point A by 10 cm to mark the new point A′ for a negative scale factor.

Step 5: Repeat for all remaining vertices:

  • Do the same for the other corners of your shape and find OB′, OC′, and OD′.

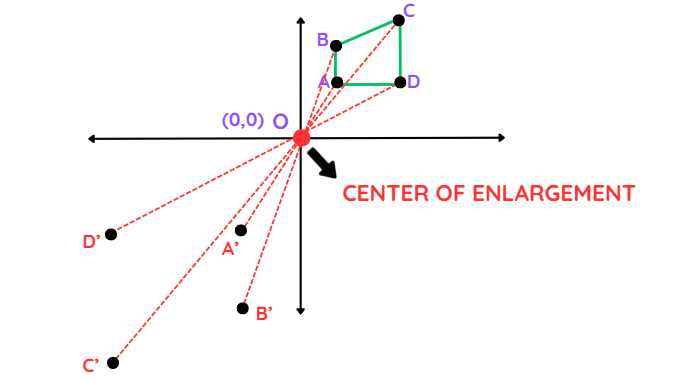
Diagram showing the enlarged, flipped version of a shape after connecting points A′, B′, C′, and D′ in a negative scale factor transformation. 

Step 6: Join the dots:

  • Connect A′, B′, C′, and D′. You’ve got an enlarged, flipped version of your shape.

Diagram showing how to extend lines from the center of enlargement at the origin to find points A′, B′, C′, and D′ for a negative scale factor transformation.

Steps to Find Enlargement Using a Negative Scale Factor (Fractional Scale Factor)

certified Physics and Maths tutor

 

 

Solved Example 2

Question: For the figure given below, find the enlargement of the object with a scale factor of -1/3 about the centre of enlargement at the point (1,1).

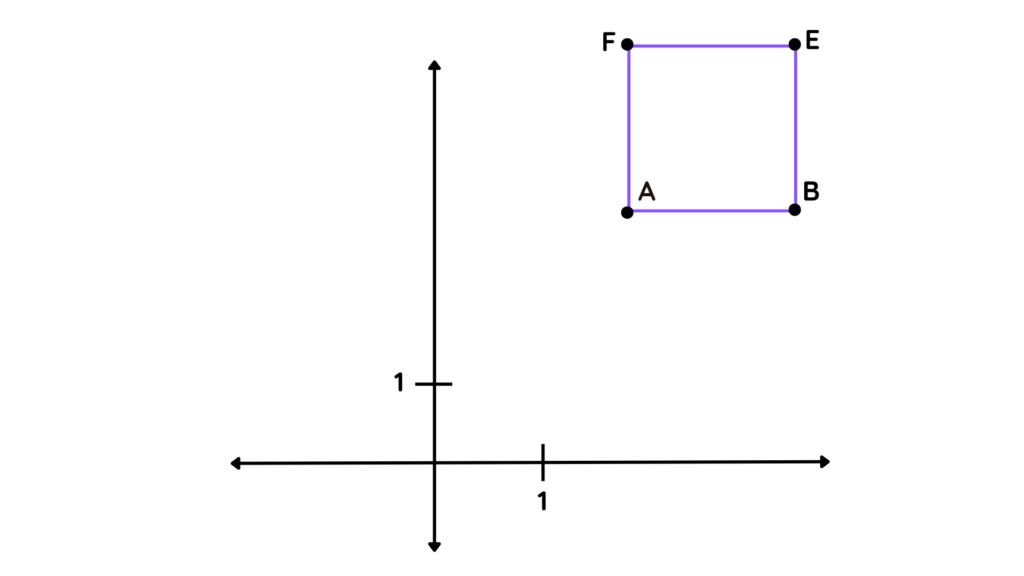
Solution: 

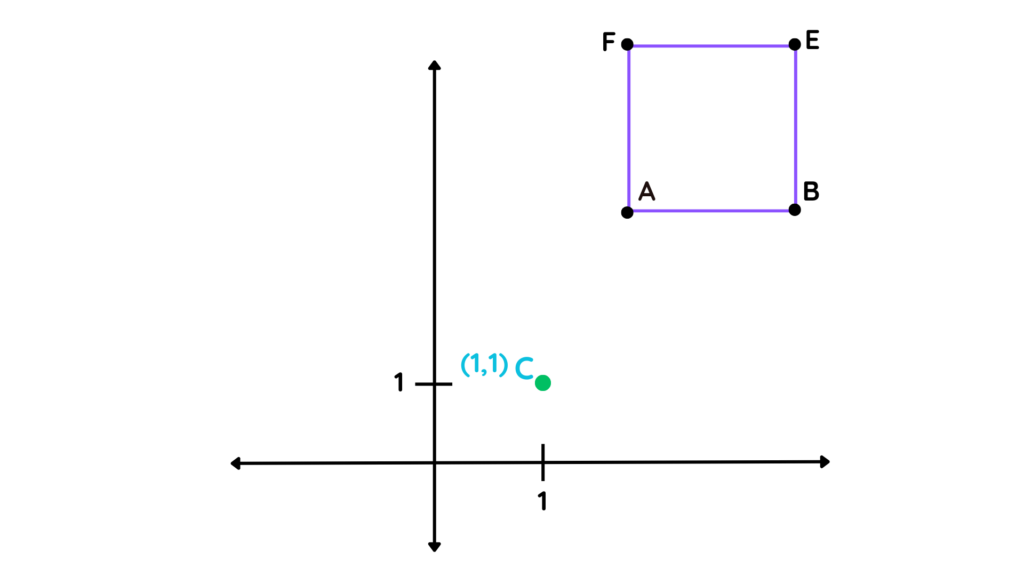
Step 1: Mark the centre of enlargement:

  • This time, we are given the point (1,1) as the centre of enlargement. Lets mark it C this time.

Diagram showing the center of enlargement marked at the point (1,1) for a transformation using a negative scale factor

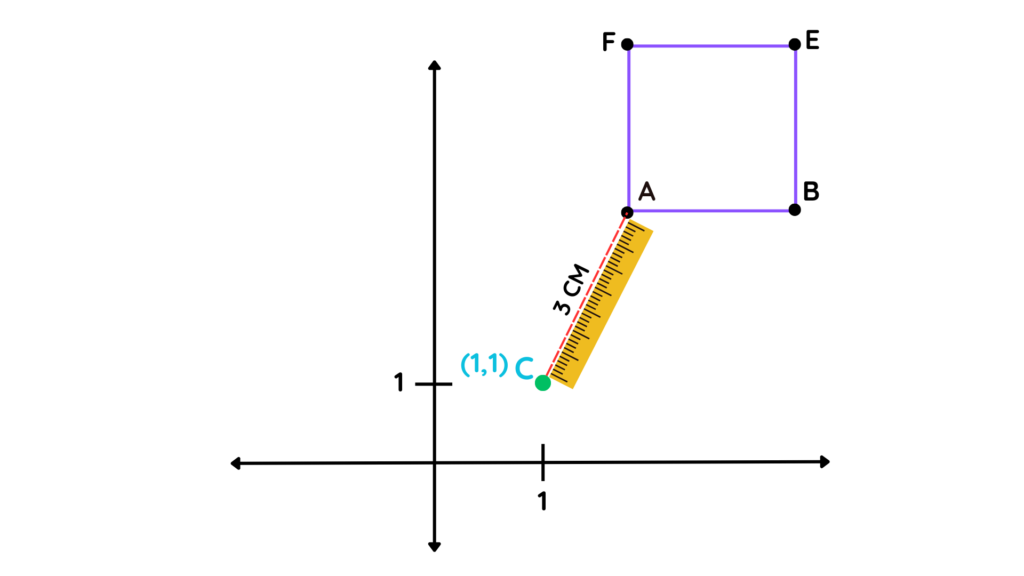
Step 2: Take a ruler and measure the distance from the centre of enlargement to one vertex of the shape.

  • Choose any vertex and call it A. Measure the distance between (1,1) and A.
  • Suppose it comes out to be 3 cm.

Diagram showing how to measure the distance from the center of enlargement at (1,1) to vertex A for a negative scale factor transformation

Step 3: Multiply by the scale factor:

  • Again, ignoring the minus sign, multiply 3 cm by 1/3

3 × 1/3 = 1 cm

Step 4: Extend the line:

  • Extend the line CA by 1 cm TO THE OTHER SIDE of the centre (1,1), and mark the point A′ there.

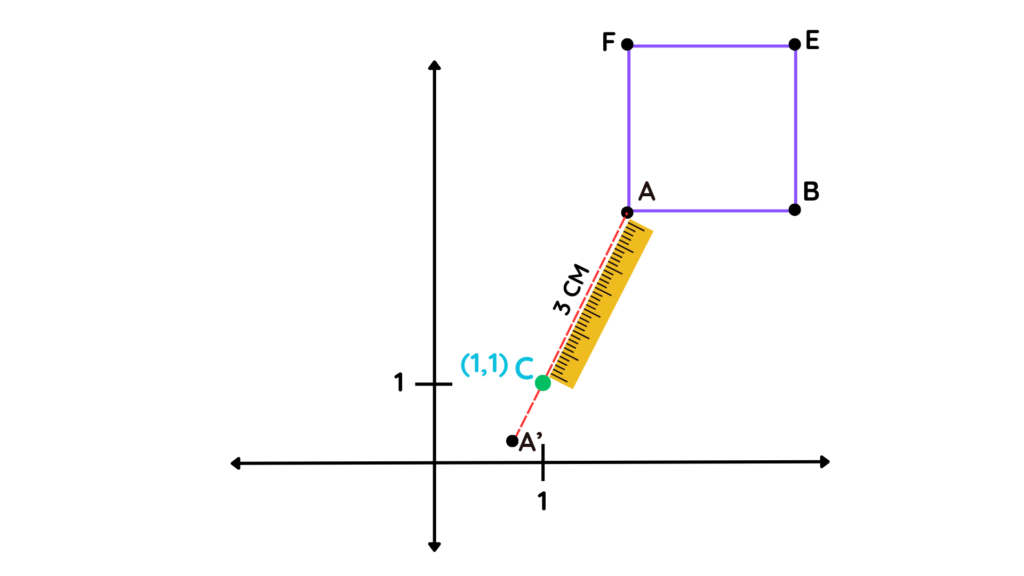
Diagram showing the extension of line CA by 1 cm to the opposite side of the center of enlargement at (1,1), marking the new point A′ for a negative scale factor.

Step 5: Repeat for all remaining vertices:

  • Do the same for the other corners of your shape and get B′, E′, and F′.

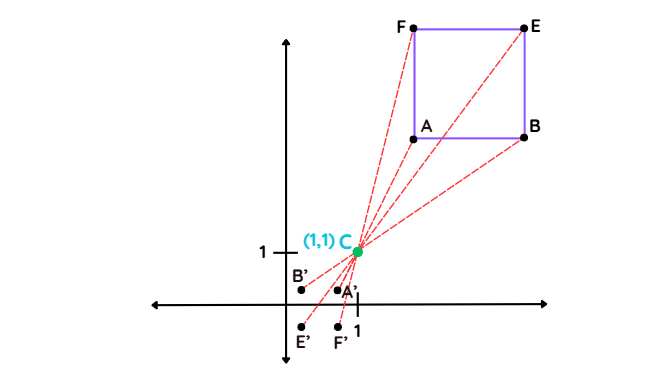
Diagram showing the transformation of all vertices A, B, E, and F to their corresponding points A′, B′, E′, and F′ using a negative scale factor centered at (1,1).

Step 6: Join the dots:

  • Connect A′, B′, E′, and F′. You’ve got an enlarged, flipped version of your shape.

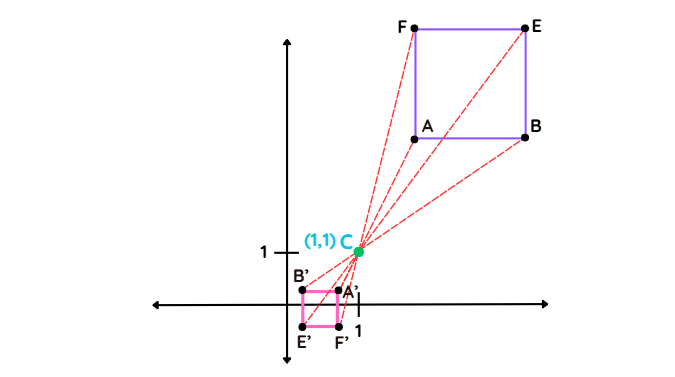
Diagram showing the connection of points A′, B′, E′, and F′ to form the enlarged, flipped version of the original shape in a negative scale factor transformation centered at (1,1).

  • Here, the steps are almost the same; the only difference is that now the lengths OA′, OB′, OE′, and OF′ are smaller than the original lengths, and the flipped shape is also smaller.

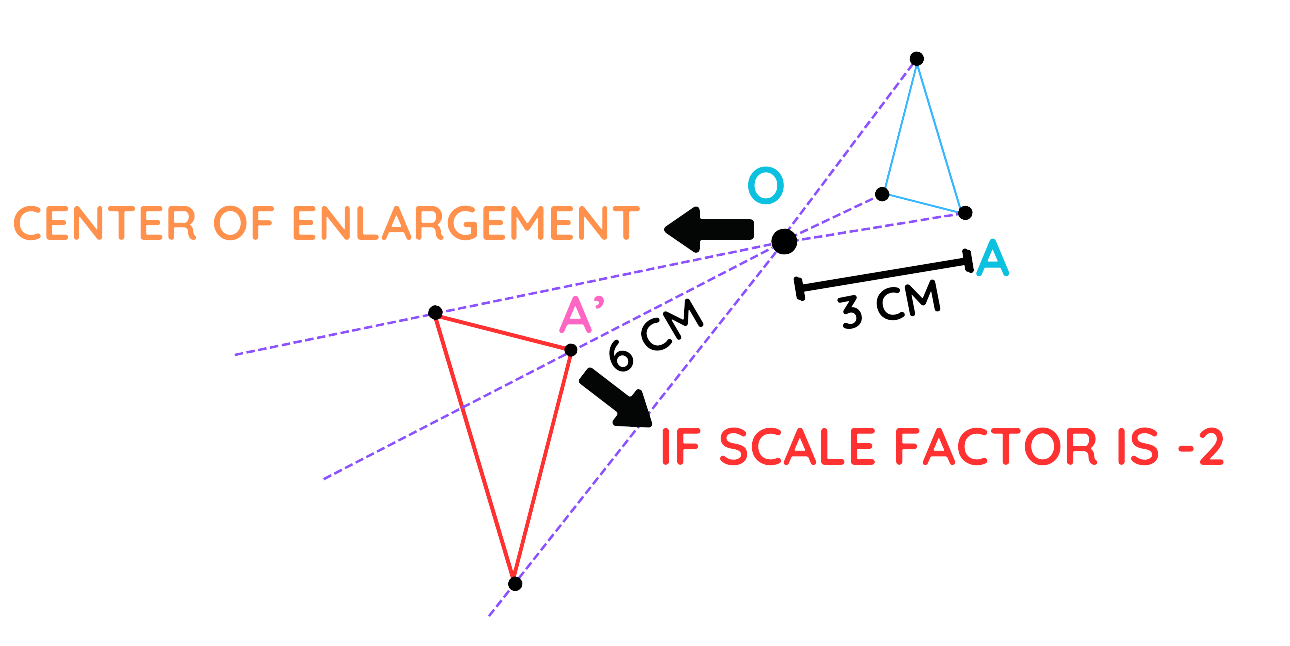
What Is The Difference Between Positive And Negative Scale Factors For Enlargement?

  • As seen in the example above, with negative scale factors, we extend the line to the opposite side of the centre of enlargement.

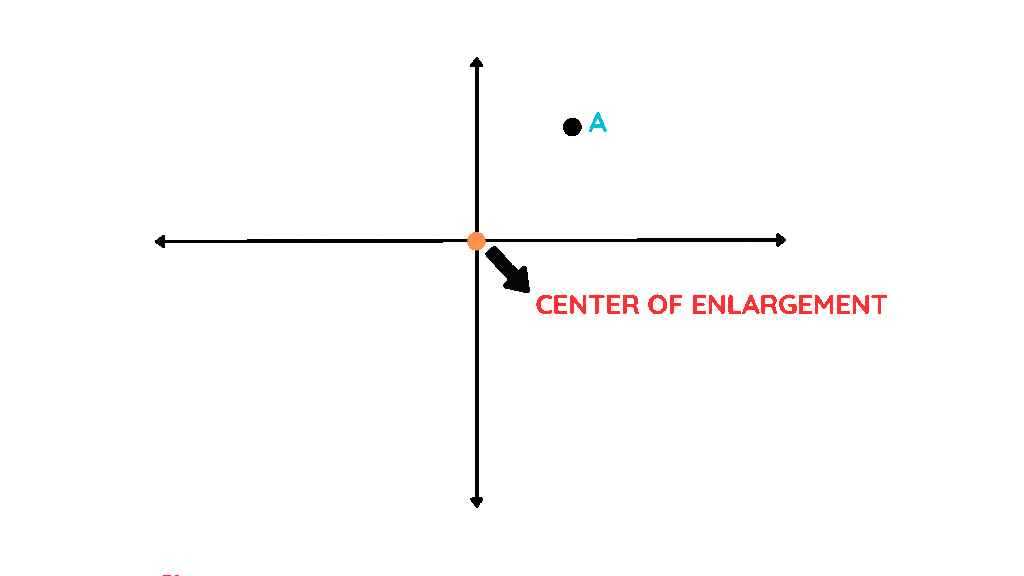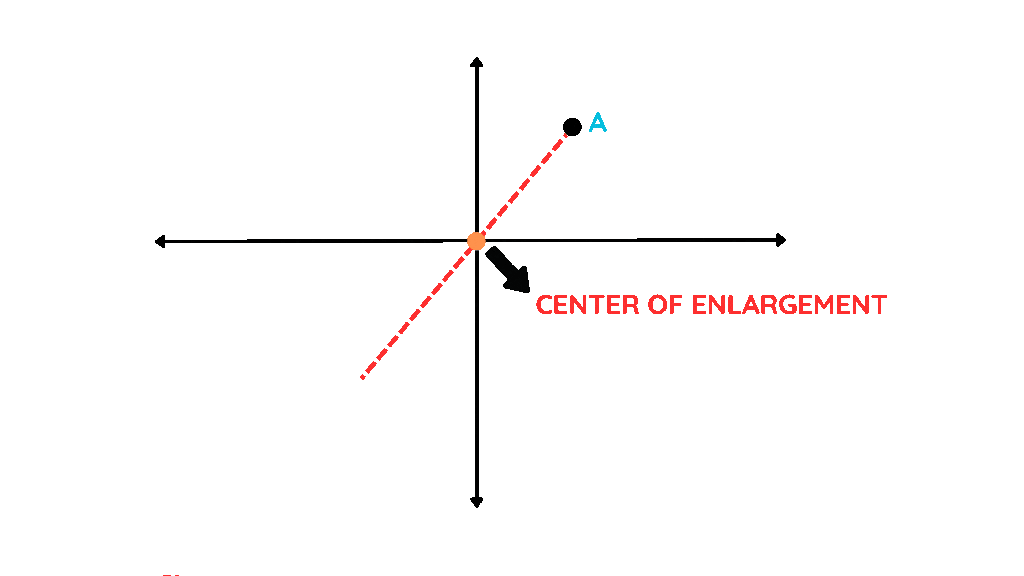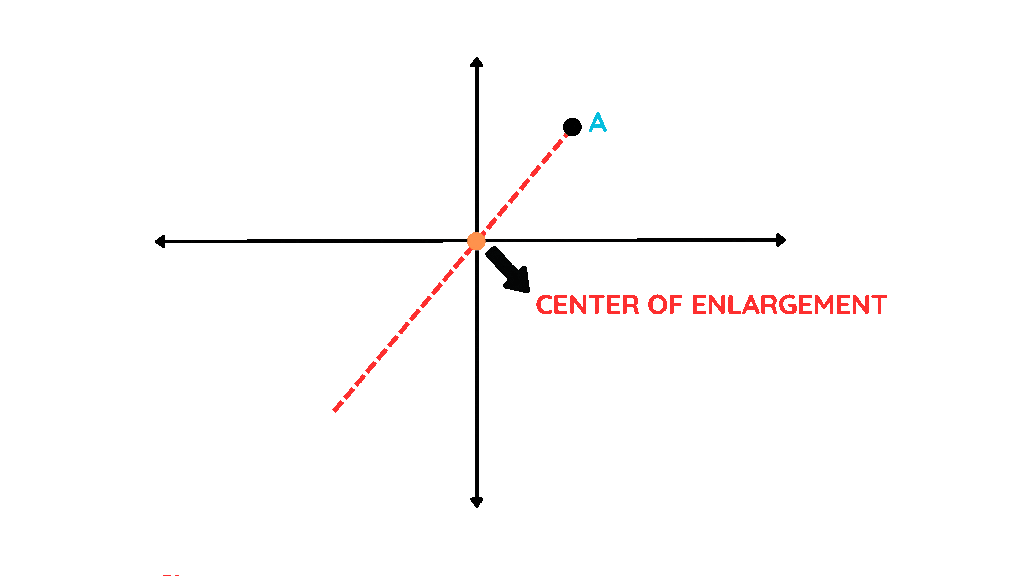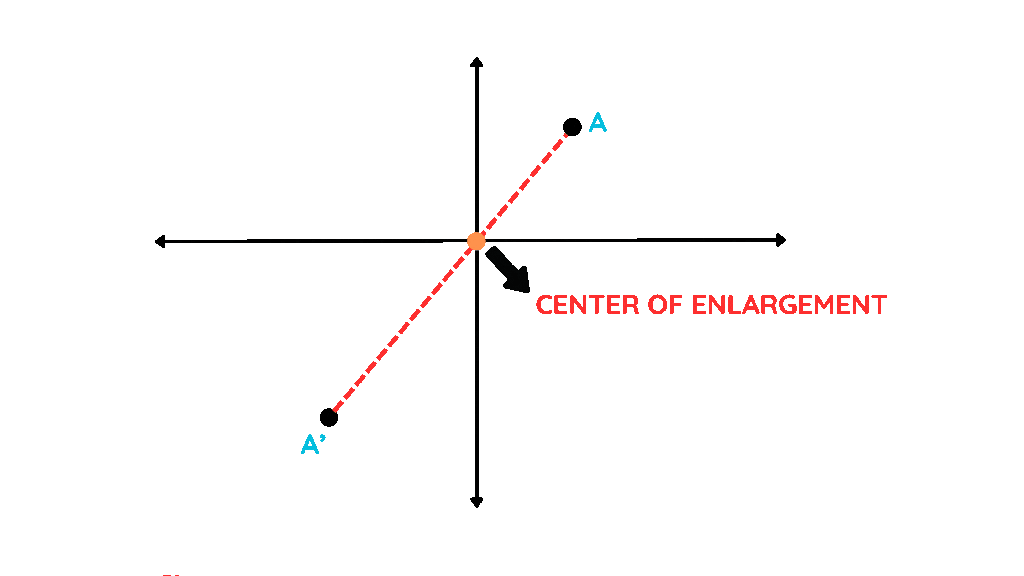
  • However, with positive scale factors, the line is extended to the same side of the centre of enlargement.

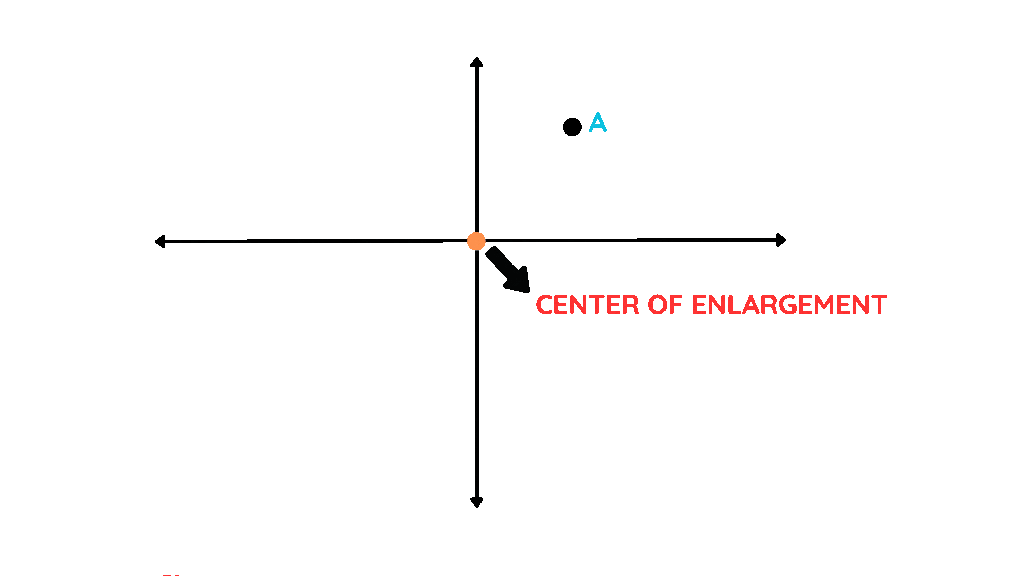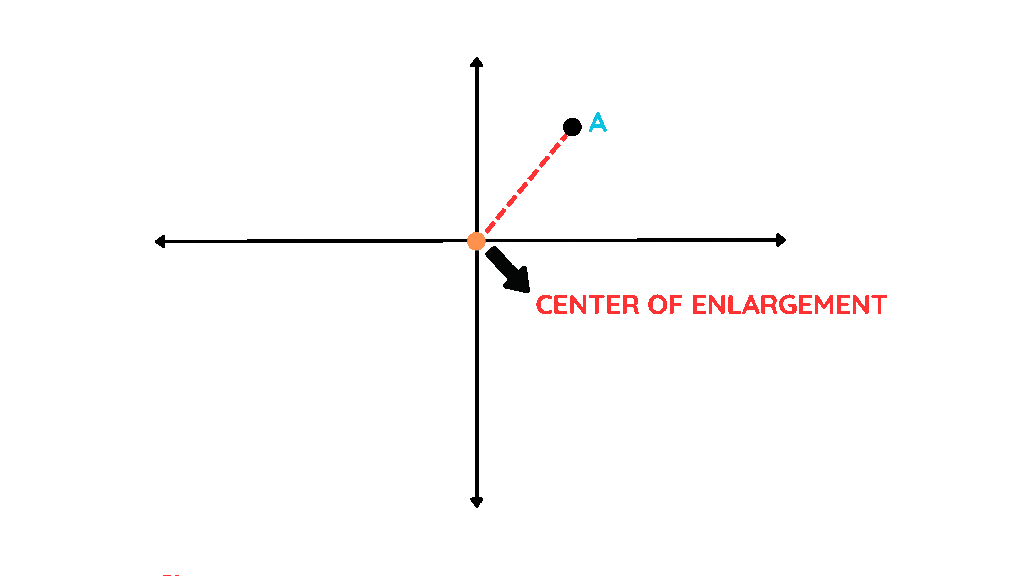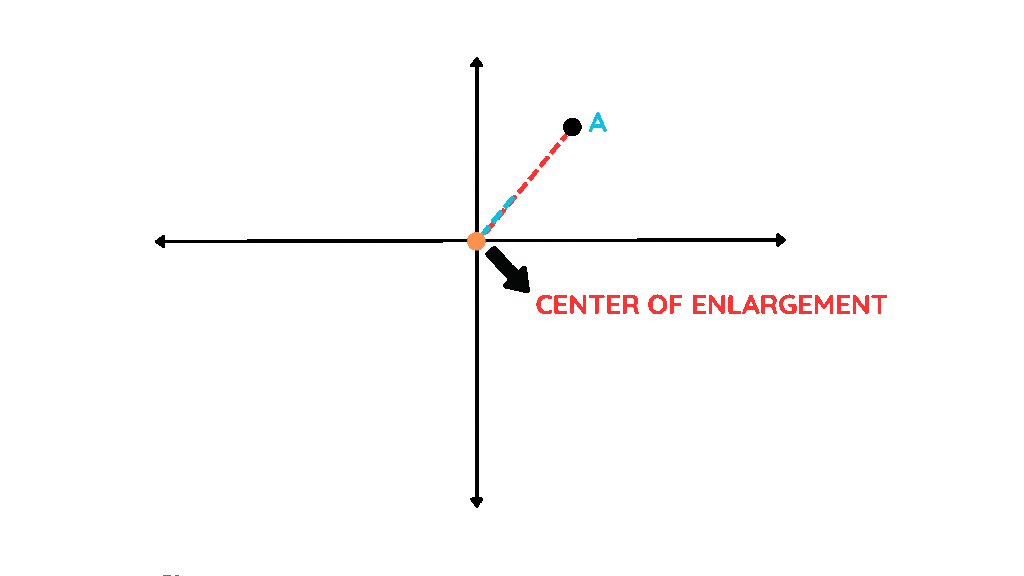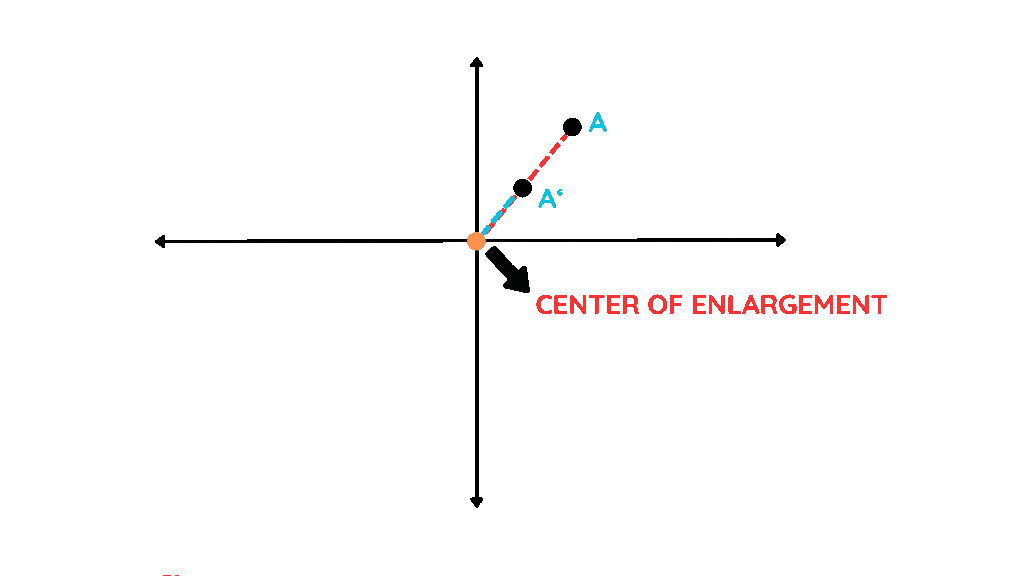
Positive Scale Factor

  • The image stays on the same side of the centre of enlargement as the original shape.
  • The shape is resized but keeps its original orientation (it doesn’t flip).
  • Example: If the scale factor is 2, the image is twice as large as the original shape, and it remains on the same side of the centre of enlargement.

Diagram showing the effect of a positive scale factor of +2 on a shape, enlarging it to twice its size while maintaining its orientation on the same side of the center of enlargement

Negative Scale Factor

  • The image appears on the opposite side of the centre of enlargement.
  • The shape is resized and flipped upside down.
  • Example: If the scale factor is -2, the image is twice as large as the original, but it’s on the opposite side and flipped.

Practice Questions and Answers on
Enlargement Using a Negative Scale Factor

Question 1: Point P(4, 6) is enlarged with a negative scale factor of -2 from the center of enlargement (0, 0). Find the coordinates of the new point.

Question 2: For the figure given below, Enlarge the rectangle by a scale factor of -3 with the center of enlargement at (0, 0). Determine the coordinates of the enlarged rectangle.

Question 3: The center of enlargement is (2, 2), and a square with vertices A(3, 3), B(5, 3), C(5, 5), and D(3, 5) is enlarged by a scale factor of -1. Find the coordinates of the vertices of the enlarged square.

Question 4: For the figure given below, Enlarge the triangle using a negative scale factor of -1.5 with the center of enlargement at (1, 1). Find the coordinates of the image.

Question 5: Point A(5, 7) is enlarged by a scale factor of -4 with the center of enlargement at (1, 2).

Question 6: A triangle has vertices X(2, 2), Y(6, 2), and Z(4, 6). It is enlarged by a scale factor of -2, with the center of enlargement at (3, 3).

Question 7: For the figure given below, It is enlarged by a scale factor of -1.5 from the center of enlargement (2, 2).

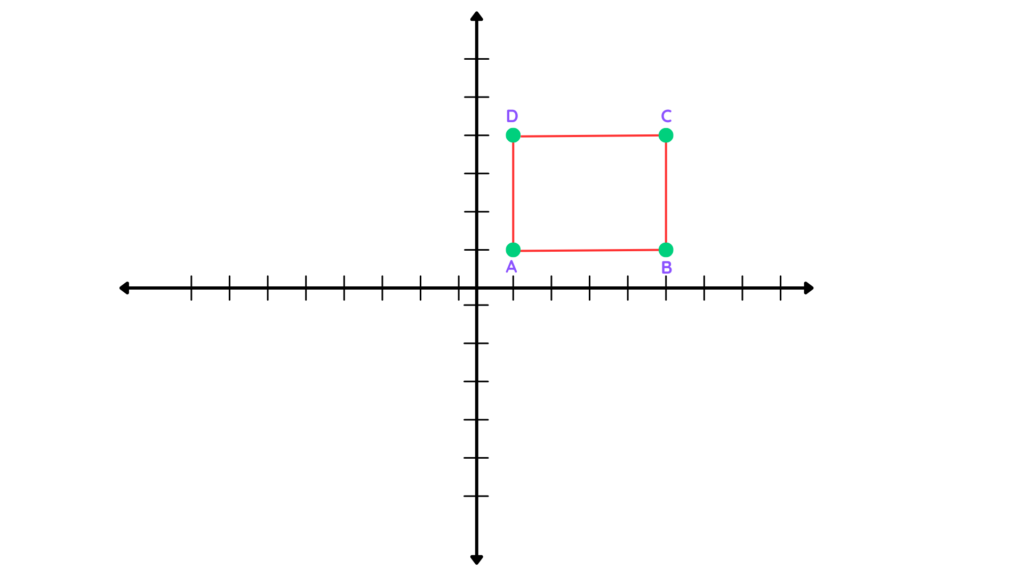
Question 8: A pentagon has vertices P(2, 3), Q(4, 5), R(6, 3), S(5, 1), and T(3, 1). It is enlarged by a scale factor of -0.5 with the center of enlargement at (3, 3).

Question 9: A triangle has vertices P(3, 2), Q(7, 2), and R(5, 5). It is enlarged by a negative scale factor of -2 with the center of enlargement at (4, 4). Find the coordinates of the enlarged triangle.

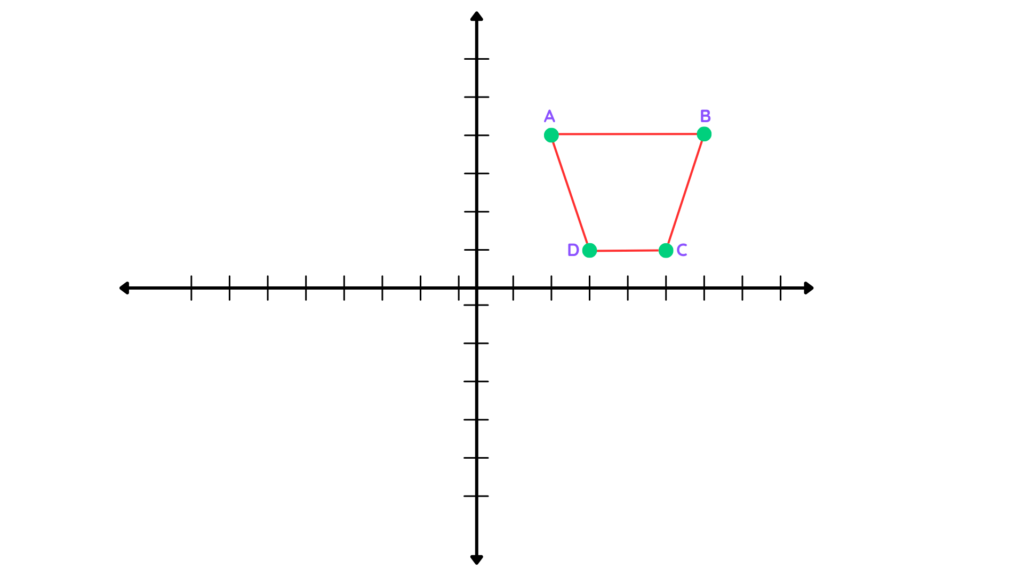
Question 10: For the figure given below, It is enlarged by a negative scale factor of -3 with the center of enlargement at (4, 3). Find the coordinates of the enlarged trapezium.

Solutions

Question 1: 

Step #1: Given:

    • The original point is P(4, 6).
    • The center of enlargement is (0, 0).
    • The scale factor is -2.

Step #2: Find the movement from the center to the point:

  • From (0, 0) to (4, 6), the point moves 4 units to the right and 6 units up.

Step #3: Apply the scale factor:

  • Multiply the movement by -2:
  • 4 units to the right becomes 8 units to the left.
  • 6 units up becomes 12 units down.

Step #4: Find the new position:

  • Starting at (0, 0), move 8 units to the left and 12 units down.
  • This gives the new position (-8, -12).

Step #5: Answer:

  • The coordinates of the new point are (-8, -12).

 

Question 2:

Step #1: Given:

  • Original vertices: A(2, 3), B(6, 3), C(6, 7), D(2, 7).
  • Center of enlargement: (0, 0).
  • Scale factor: -3.

Step #2: Find the vector for each point:

  • A: (2, 3).
  • B: (6, 3).
  • C: (6, 7).
  • D: (2, 7).

Step #3: Apply the scale factor (-3):

  • A: (2 × -3, 3 × -3) = (-6, -9).
  • B: (6 × -3, 3 × -3) = (-18, -9).
  • C: (6 × -3, 7 × -3) = (-18, -21).
  • D: (2 × -3, 7 × -3) = (-6, -21).

Step #4: New coordinates:

  • A'(-6, -9), B'(-18, -9), C'(-18, -21), D'(-6, -21).

 

Question 3:

Step #1: Given:

  • Original vertices: A(3, 3), B(5, 3), C(5, 5), D(3, 5).
  • Center of enlargement: (2, 2).
  • Scale factor: -1.

Step #2: Find the vector from the center to each vertex:

  • A: (3 – 2, 3 – 2) = (1, 1).
  • B: (5 – 2, 3 – 2) = (3, 1).
  • C: (5 – 2, 5 – 2) = (3, 3).
  • D: (3 – 2, 5 – 2) = (1, 3).

Step #3: Apply the scale factor (-1):

  • A: (-1 × 1, -1 × 1) = (-1, -1).
  • B: (-1 × 3, -1 × 1) = (-3, -1).
  • C: (-1 × 3, -1 × 3) = (-3, -3).
  • D: (-1 × 1, -1 × 3) = (-1, -3).

Step #4: Find the new coordinates:

  • A'(2 + (-1), 2 + (-1)) = (1, 1).
  • B'(2 + (-3), 2 + (-1)) = (-1, 1).
  • C'(2 + (-3), 2 + (-3)) = (-1, -1).
  • D'(2 + (-1), 2 + (-3)) = (1, -1).

Step #5: Answer:

  • A'(1, 1), B'(-1, 1), C'(-1, -1), D'(1, -1).

 

Question 4:

Step #1: Given:

  • Original vertices: P(2, 4), Q(4, 6), R(6, 4).
  • Center of enlargement: (1, 1).
  • Scale factor: -1.5.

Step #2: Find the vector from the center to each vertex:

  • P: (2 – 1, 4 – 1) = (1, 3).
  • Q: (4 – 1, 6 – 1) = (3, 5).
  • R: (6 – 1, 4 – 1) = (5, 3).

Step #3: Apply the scale factor (-1.5):

  • P: (-1.5 × 1, -1.5 × 3) = (-1.5, -4.5).
  • Q: (-1.5 × 3, -1.5 × 5) = (-4.5, -7.5).
  • R: (-1.5 × 5, -1.5 × 3) = (-7.5, -4.5).

Step #4: Find the new coordinates:

  • P'(1 + (-1.5), 1 + (-4.5)) = (-0.5, -3.5).
  • Q'(1 + (-4.5), 1 + (-7.5)) = (-3.5, -6.5).
  • R'(1 + (-7.5), 1 + (-4.5)) = (-6.5, -3.5).

Step #5: Answer:

  • P'(-0.5, -3.5), Q'(-3.5, -6.5), R'(-6.5, -3.5).

 

Question 5: 

Step #1: Given:

  • Original point: A(5, 7).
  • Center of enlargement: (1, 2).
  • Scale factor: -4.

Step #2: Find the movement from the center to the point:

  • From (1, 2) to (5, 7):
  • Move 4 units right (5 – 1 = 4).
  • Move 5 units up (7 – 2 = 5).

Step #3: Apply the scale factor:

  • Multiply each movement by -4:
  • Right becomes left: 4 × -4 = -16.
  • Up becomes down: 5 × -4 = -20.

Step #4: Find the new position:

  • From (1, 2), move -16 units left and -20 units down:
  • New position: (-15, -18).

Step #5: Answer:

  • The coordinates of the new point are (-15, -18).

 

Question 6: 

Step #1: Given:

  • Original vertices: X(2, 2), Y(6, 2), Z(4, 6).
  • Center of enlargement: (3, 3).
  • Scale factor: -2.

Step #2: Find the movement for each vertex:

  • For X(2, 2):
  • Move 1 left and 1 down (from (3, 3)).
  • For Y(6, 2):
  • Move 3 right and 1 down (from (3, 3)).
  • For Z(4, 6):
  • Move 1 right and 3 up (from (3, 3)).

Step #3: Apply the scale factor (-2):

  • For X:
  • Left becomes right: 1 × -2 = 2.
  • Down becomes up: 1 × -2 = 2.
  • For Y:
  • Right becomes left: 3 × -2 = -6.
  • Down becomes up: 1 × -2 = 2.
  • For Z:
  • Right becomes left: 1 × -2 = -2.
  • Up becomes down: 3 × -2 = -6.

Step #4: Find the new coordinates:

  • X’: (3 + 2, 3 + 2) = (5, 5).
  • Y’: (3 – 6, 3 + 2) = (-3, 5).
  • Z’: (3 – 2, 3 – 6) = (1, -3).

Step #5: Answer:

  • The coordinates of the enlarged triangle are X'(5, 5), Y'(-3, 5), Z'(1, -3).

 

Question 7: 

Step #1: Given:

  • Original vertices: A(1, 1), B(5, 1), C(5, 4), D(1, 4).
  • Center of enlargement: (2, 2).
  • Scale factor: -1.5.

Step #2: Find the movement for each vertex:

  • For A(1, 1): Move 1 left and 1 down (from (2, 2)).
  • For B(5, 1): Move 3 right and 1 down (from (2, 2)).
  • For C(5, 4): Move 3 right and 2 up (from (2, 2)).
  • For D(1, 4): Move 1 left and 2 up (from (2, 2)).

Step #3: Apply the scale factor (-1.5):

  • For A:
    • Multiply -1.5 by each movement:
    • Left becomes right: 1 × -1.5 = 1.5 right.
    • Down becomes up: 1 × -1.5 = 1.5 up.
  • For B:
    • Right becomes left: 3 × -1.5 = -4.5 left.
    • Down becomes up: 1 × -1.5 = 1.5 up.
  • For C:
    • Right becomes left: 3 × -1.5 = -4.5 left.
    • Up becomes down: 2 × -1.5 = -3 down.
  • For D:
    • Left becomes right: 1 × -1.5 = 1.5 right.
    • Up becomes down: 2 × -1.5 = -3 down.

Step #4: Find the new coordinates:

  • A’: (2 + 1.5, 2 + 1.5) = (3.5, 3.5).
  • B’: (2 – 4.5, 2 + 1.5) = (-2.5, 3.5).
  • C’: (2 – 4.5, 2 – 3) = (-2.5, -1).
  • D’: (2 + 1.5, 2 – 3) = (3.5, -1).

Step #5: Answer:

  • The coordinates of the enlarged rectangle are A'(3.5, 3.5), B'(-2.5, 3.5), C'(-2.5, -1), D'(3.5, -1).

 

Question 8: 

Step #1: Given:

  • Original vertices: P(2, 3), Q(4, 5), R(6, 3), S(5, 1), T(3, 1).
  • Center of enlargement: (3, 3).
  • Scale factor: -0.5.

Step #2: Find the movement for each vertex:

  • For P(2, 3): Move 1 left and 0 up (from (3, 3)).
  • For Q(4, 5): Move 1 right and 2 up (from (3, 3)).
  • For R(6, 3): Move 3 right and 0 up (from (3, 3)).
  • For S(5, 1): Move 2 right and 2 down (from (3, 3)).
  • For T(3, 1): Move 0 right and 2 down (from (3, 3)).

Step #3: Apply the scale factor (-0.5):

  • For P:
    • Left becomes right: 1 × -0.5 = 0.5 right.
    • No vertical movement: 0 × -0.5 = 0.
  • For Q:
    • Right becomes left: 1 × -0.5 = -0.5 left.
    • Up becomes down: 2 × -0.5 = -1.
  • For R:
    • Right becomes left: 3 × -0.5 = -1.5 left.
    • No vertical movement: 0 × -0.5 = 0.
  • For S:
    • Right becomes left: 2 × -0.5 = -1 left.
    • Down becomes up: 2 × -0.5 = 1 up.
  • For T:
    • No horizontal movement: 0 × -0.5 = 0.
    • Down becomes up: 2 × -0.5 = 1 up.

Step #4: Find the new coordinates:

  • P’: (3 + 0.5, 3 + 0) = (3.5, 3).
  • Q’: (3 – 0.5, 3 – 1) = (2.5, 2).
  • R’: (3 – 1.5, 3 + 0) = (1.5, 3).
  • S’: (3 – 1, 3 + 1) = (2, 4).
  • T’: (3 + 0, 3 + 1) = (3, 4).

Step #5: Answer:

  • The coordinates of the enlarged pentagon are P'(3.5, 3), Q'(2.5, 2), R'(1.5, 3), S'(2, 4), T'(3, 4).

 

Question 9: 

Step #1: Given:

  • Original vertices: P(3, 2), Q(7, 2), R(5, 5).
  • Center of enlargement: (4, 4).
  • Scale factor: -2.

Step #2: Find the movement for each vertex from the center:

  • For P(3, 2):
    • Move 1 unit left and 2 units down from (4, 4)
  • For Q(7, 2):
    • Move 3 units right and 2 units down from (4, 4).
  • For R(5, 5):
    • Move 1 unit right and 1 unit up from (4, 4).

Step #3: Apply the scale factor (-2):

  • For P:
    • Left becomes right: 1 × -2 = 2 units right.
    • Down becomes up: 2 × -2 = 4 units up.
  • For Q:
    • Right becomes left: 3 × -2 = 6 units left.
    • Down becomes up: 2 × -2 = 4 units up.
  • For R:
    • Right becomes left: 1 × -2 = 2 units left.
    • Up becomes down: 1 × -2 = 2 units down.

       

Step #4: Find the new coordinates:

  • For P: Start at (4, 4), move 2 units right and 4 units up:
    New position: (6, 8).
  • For Q: Start at (4, 4), move 6 units left and 4 units up:
    New position: (-2, 8).
  • For R: Start at (4, 4), move 2 units left and 2 units down:
    New position: (2, 2)

Step #5: Answer:

  • The coordinates of the enlarged triangle are P'(6, 8), Q'(-2, 8), R'(2, 2).

 

Question 10: 

Step #1: Given:

  • Original vertices: A(2, 4), B(6, 4), C(5, 1), D(3, 1).
  • Center of enlargement: (4, 3).
  • Scale factor: -3.

Step #2: Find the movement for each vertex from the center:

  • For A(2, 4):
    • Move 2 units left and 1 unit up from (4, 3).
  • For B(6, 4):
    • Move 2 units right and 1 unit up from (4, 3).
  • For C(5, 1):
    • Move 1 unit right and 2 units down from (4, 3).
  • For D(3, 1):
    • Move 1 unit left and 2 units down from (4, 3).

Step #3: Apply the scale factor (-3):

  • For A:
    • Left becomes right: 2 × -3 = 6 units right.
    • Up becomes down: 1 × -3 = 3 units down.
  • For B:
    • Right becomes left: 2 × -3 = 6 units left.
    • Up becomes down: 1 × -3 = 3 units down.
  • For C:
    • Right becomes left: 1 × -3 = 3 units left.
    • Down becomes up: 2 × -3 = 6 units up.
  • For D:
    • Left becomes right: 1 × -3 = 3 units right.
    • Down becomes up: 2 × -3 = 6 units up.

Step #4: Find the new coordinates:

  • For A: Start at (4, 3), move 6 units right and 3 units down:
    New position: (10, 0).
  • For B: Start at (4, 3), move 6 units left and 3 units down:
    New position: (-2, 0).
  • For C: Start at (4, 3), move 3 units left and 6 units up:
    New position: (1, 9).
  • For D: Start at (4, 3), move 3 units right and 6 units up:
    New position: (7, 9).

Step # 5: Answer:

  • The coordinates of the enlarged trapezium are A'(10, 0), B'(-2, 0), C'(1, 9), and D'(7, 9).
Request for Demo Lesson

Table of Content