Direct and Inverse Proportion Graphs, Formula with Worksheet
Direct and Inverse Proportion
- ‘Direct & inverse proportion’ are the two terms about the relationship between two variables.
- These ideas are the foundation of mathematics and they are often incorporated in everyday mathematical applications.
- What is Direct and Inverse Proportion?
- Formula for Direct and Inverse Proportions
- Direct and Inverse Proportion Graphs
What is Direct and Inverse Proportion?
Direct Proportion:
- A direct proportion is a relationship between two variables that either increase or decrease at the same time and in the same numerical value.
- Thus, with the elevation of one of the variables, the second variable rises and the fall of one variable results decline of the other.
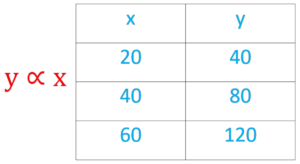
Inverse Proportion:
- Inverse proportion is a type of relationship between two variables whereby both variables change in parallel in the opposite direction, the more one of the variables increases the more the other one decreases.
- So, to say differently, the increase of one variable results in the decrease of the other and vice versa.
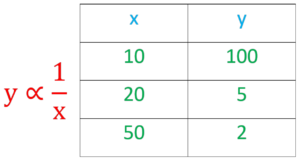
Formula for Direct and Inverse Proportions
For Direct Proportion,
- The equation is y=kx, where y represents the dependent variable, x is the independent variable and k is the rate of proportionality.
For Inverse Proportion,
- The equation is y = k/x, and it has y dependent and x independent variables while k is the constant of proportionality.
Steps to Solve Questions with Direct Proportion
- Step #1: Identify the two variables and demonstrate if they have a direct proportional correlation.
- Step #2: The formula for the constant of proportionality defining a linear function as y = kx is used to calculate the value of the constant (k).
- Step #3: As x and y change their value and substitute them in the formula then the value of k is calculated.
- Step #4: After you have discovered the value of k, use it to derive x or y, if there is any unknown value in x or y.
Solved Example:
Question 1: If a box of 10 pencils is $2, what is the price of a box of 20 pencils?
Solution:
- Step #1: These are two variables, which are the pencils’ count and price.
- Step #2: We are aware of the direct proportionality, which ensures that we can use the formula y = kx.
- Step #3: Substituting the values we get
2 = 10k,
which gives
k = 0.2
- Step #4: Through the value of k, we can find the price for 20 pencils. Thus.
y = 0.2 x 20
= $4.
Question 2: A force is directly proportional to the square of the distance between two objects. If a force of 12 N is required to move an object 4 meters away from another object, how much force is required to move the object 8 meters away?
Solution:
- Step #1: Define variables and relationships
Let F be the force required to move the object.
Let d be the distance between the objects.
The force is directly proportional to the square of the distance, so F ∝ d2.
- Step #2: Express the proportional relationship with a constant
Write the equation:
F = k x d2,
where k is the proportionality constant.
- Step #3: Use the given values to find the constant (k)
Given force (12 N) and distance (4 meters):
12 N = k x 42.
Solve for k:
k = 12 / 16 = 0.75.
- Step #4: Substitute the constant into the proportional relationship
The equation now becomes:
F = 0.75 x d2.
- Step #5: Find the force required for the new distance (8 meters)
Substitute the new distance (8 meters) into the equation:
F = 0.75 x 82.
Calculate:
F = 0.75 x 64
= 48 N.
Therefore, a force of 48 N is required to move the object 8 meters away.
Practice Questions
Question 1: If a car travels 120 miles on 6 gallons of gas, how far can it travel on 10 gallons, assuming the relationship between distance and fuel consumption is directly proportional?
Answer :Solution:
Step #1: Identify the two variables involved - distance and gallons of gas.
Step #2: Recognize the direct proportionality, represented by the formula y = kx.
Step #3: Apply the given values to the formula:
120/6 = k
Step #4: Solve for k:
K = 20
Step #5: Use the determined k value to find the distance for 10 gallons:
20 x 10 = 200 miles.
Question 2: If a machine produces 30 units in 5 hours, how many units can it produce in 8 hours, assuming a direct proportionality between production and time?
Answer :Solution:
Step #1: Identify the variables – units produced and time.
Step #2: Recognize the direct proportionality, represented by the formula y = kx.
Step #3: Apply the given values to the formula:
30/5 = k
Step #4: Solve for k:
K = 6
Step #5: Use the determined k value to find the units produced in 8 hours:
6 x 8 = 48 units
Steps to Solve Questions with Inverse Proportion
- Step #1: Identify the two variables and see if they have the nature of an inverse proportion.
- Step #2: Employing the formula y = k/x to obtain the constant of proportionality (k).
- Step #3: Substitute x and y for the same values in the formula and solve for the k.
- Step #4: When you have derived the value of k, you can utilize it to find out then any of the variables x or y.
Solved Example
Question 1: If it takes 6 hours for 2 workers to complete a task, how long would it take for 3 workers to complete the same task?
Solution:
- Step #1: The two variables are the number of workers and the time taken to complete the task.
- Step #2: We know that they are inversely proportional, so we can use the formula
y = k/x.
- Step #3: Substituting the values we get
6 = k/2,
which gives
k = 12.
- Step #4: Using this value of k, we can find the time taken by 3 workers as
y = 12/3
= 4 hours.
Question 2: The time taken to complete a task is inversely proportional to the square of the number of workers. If a task takes 16 hours to complete with 4 workers, how long will it take to complete the task with 8 workers?
Solution:
- Step #1: Define variables and relationships
Let T be the time taken to complete the task.
Let w be the number of workers.
The time taken is inversely proportional to the square of the number of workers, so T ∝ 1 / w2.
- Step #2: Express the inverse proportional relationship with a constant
Write the equation:
T = k / w2,
where k is the proportionality constant.
- Step #3: Use the given values to find the constant (k)
Given time (16 hours) and number of workers (4):
16 hours ∝ 1 / 42.
Solve for k:
16 hours = k / 16,
k = 16 x 16
= 256.
- Step #4: Substitute the constant into the inverse proportional relationship
The equation now becomes:
T = 256 / w2.
- Step #5: Find the time required for the new number of workers (8 workers)
Substitute the new number of workers (8) into the equation:
T = 256 / 82.
Calculate:
T = 256 / 64
= 4 hours.
Therefore, it will take 4 hours to complete the task with 8 workers.
Practice Questions
Question 1: If a water tank can be filled by 4 pipes in 2 hours, how long will it take for the tank to be filled if only 2 pipes are used, assuming an inverse proportionality between the number of pipes and the time required?
Answer :Solution:
Step #1: Identify the variables - number of pipes and time.
Step #2: Recognize the inverse proportionality, represented by the formula y = k/x
Step #3: Apply the given values to the formula:
2 = k/4
Step #4: Solve for k:
K = 8
Step #5: Use the determined k value to find the time for 2 pipes:
8/2 = 4 hours.
Question 2: If a garden can be weeded by 5 gardeners in 4 hours, how many hours will it take for 8 gardeners to complete the same weeding task, assuming an inverse proportionality between the number of gardeners and the time required?
Answer :Solution:
Step #1: Identify the variables - number of gardeners and time.
Step #2: Recognize the inverse proportionality, represented by the formula y = k/x
Step #3: Apply the given values to the formula:
4 = k/5
Step #4: Solve for k:
K = 20
Step #5: Use the determined k value to find the time for 8 gardeners:
20/8 = 2.5 hours.
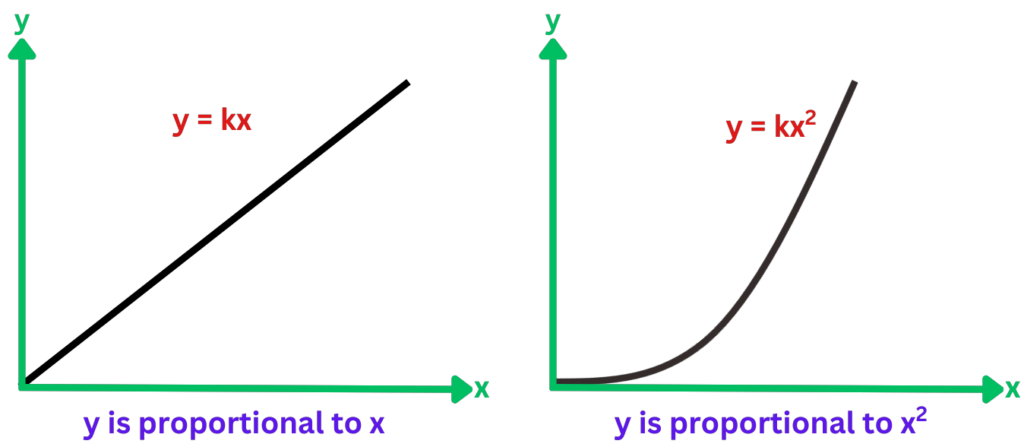
Direct and Inverse Proportion Graphs
Direct Proportion:
- On a direct proportion graph, a straight line crosses the origin. It means that if a certain variable is going up, the other one is going up proportionally.
- The curve of the directly proportional graph is the constant of proportionality. The larger the slope, the more the constant of proportion.
Inverse Proportion Graphs
Inverse Proportion:
- A hyperbola is demonstrated by the association between the x and y-axis, which approaches and never touches the x or y-axis.
- This implies that with the rise of one variable the other variable will go down proportionally as well.
- The more graph is closer to either the x or y-axis, the bigger the constant of proportionality is.
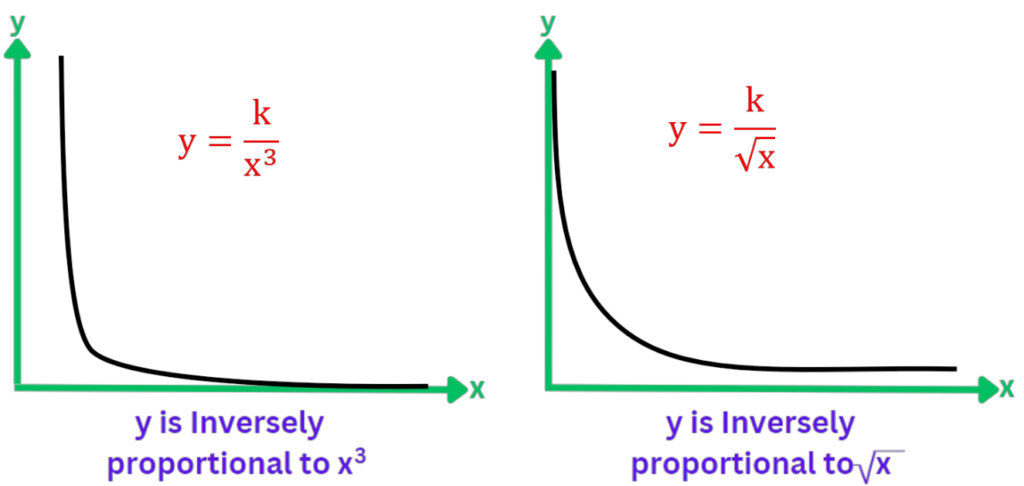
In direct proportion graphs, the y-intercept is always zero, while in inverse proportion graphs, the x and y intercepts are never zero.
Conclusion
Such graphs us as a direct and inverse proportional tool to model real-world relationships.
Preferable, they can present a relationship between distance travelled and time taken during constant-speed driving along the travel.
Also, these diagrams are suitable for demonstrating the proportion between the amount of ingredients and the number of servings in cooking recipes.
Worksheet on Direct and Inverse Proportion
Question 1: Suppose x and y are in inverse proportion. If y = 12 then x = 4, find the value of y when x = 8..
Question 2: If two cardboard boxes occupy 500 cubic centimetres of space, then how much space is required to keep 200 such boxes?
Question 3: If 35 men can finish a piece of work in 8 days, in how many days 20 men complete the same work?
Question 4: If 270 kg of corn would feed 42 horses for 21 days, for how many days would 360 kg of corn feed 21 horses?

