Decimal Recurring to Fraction

Practice Questions
Downloads

Introduction

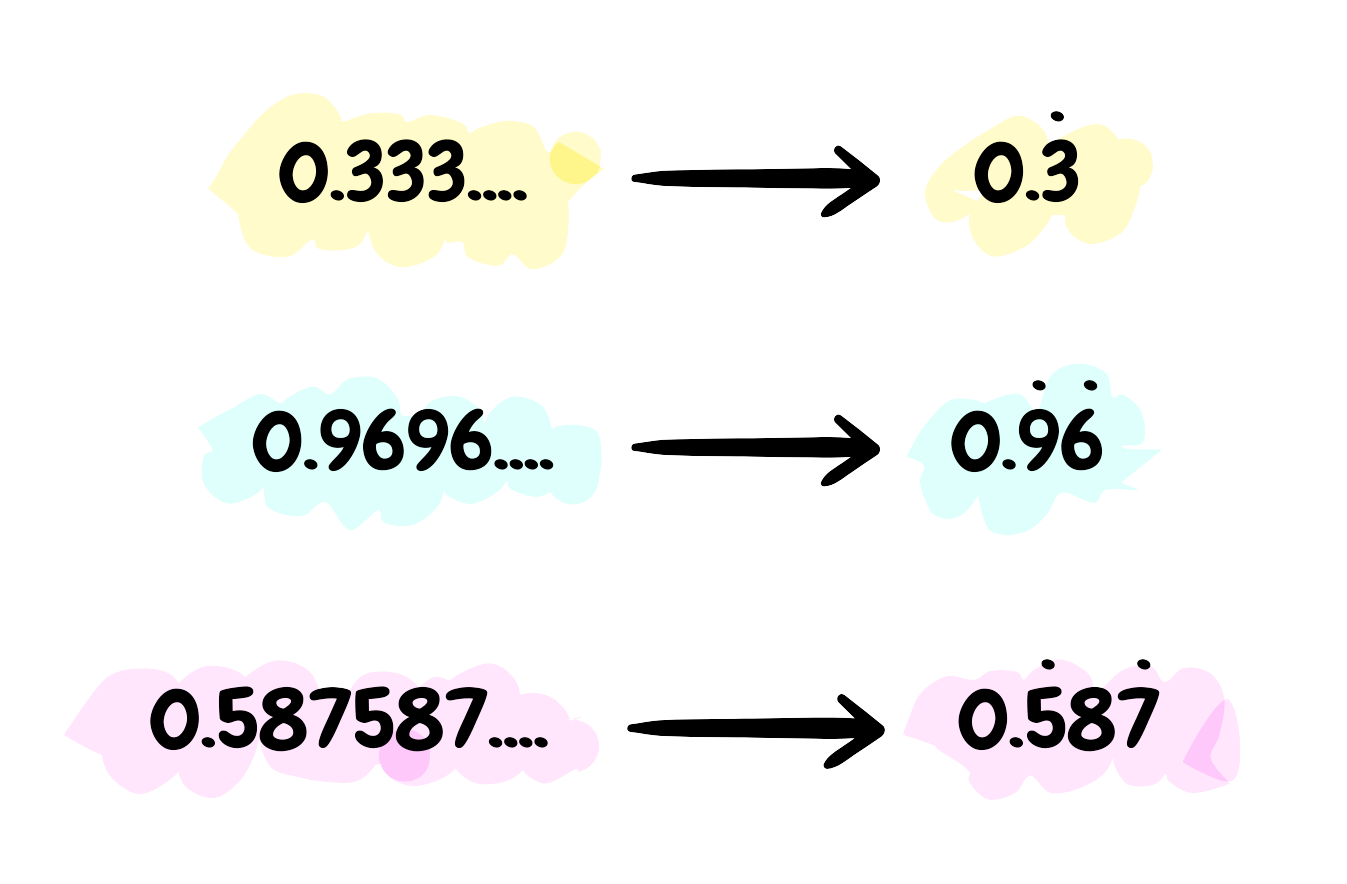
  • A Recurring Decimal is denoted with a dot over the number and is any decimal in which the digits repeat themselves.

Types of Recurring Decimals

Pure Recurring Decimals:

  • Decimal where all the digits after the decimal point repeat indefinitely.

Examples:

  • 0.333…
  • 0.7474….
  • 0.4545….
  • 0.98549854….

Mixed Recurring Decimals:

  • After the decimal point, some digits do not repeat, and a sequence of digits starts repeating indefinitely after the non-repeating part.

Examples:

  • 0.23434….
  • 0.165858….
  • 0.2358989….
  • 0.7852222….

How to Convert Recurring Decimals to Fractions (Type 1)

Type 1: Converting Pure Recurring Decimals to Fraction:

Step#1: Take your term as x.

Step#2: Multiply both sides by 10n (where n is the number of repeating digits).

  • Multiply 10 for 1 Recurring Decimal.

Example: 

For 0.333…, there is only 1 digit repeat, so multiply by

101 = 10

So, 10x = 3.333…

  • Multiply 100 for 2 Recurring Decimal.

Example:

For 0.2929…, there is 2 digits repeat, so multiply by

102 = 100

So, 100x = 29.2929…

  • Multiply 1000 for 3 Recurring Decimal.

Example:

For 0.816816…, there is 3 digits repeat, so multiply by

103 =1000

So, 1000x = 816.816816…

Step#3: Subtract original equation from new equation to eliminate the repeating part.

Step#4: Solve for x and simplify fraction, if possible.

How to Convert Recurring Decimals to Fractions (Type 2)

Type 2: Converting Mixed Recurring Decimals to Fraction:

Step#1: Take your term as x.

Step#2: Multiply both sides by 10 (where m is the number of non-repeating digits).

Step #3: Multiply both sides by 10n (where n is the number of repeating digits) to shift the Decimal.

Step#4: Subtract original equation from new equation to eliminate the repeating part.

Step#5: Solve for x and simplify fraction, if possible. 

certified Physics and Maths tutorSolved Example

Problem: Convert 0.12323… into Fraction.

Solution: 

Step #1: Let x = 0.12323…

Step #2: Multiply both side by 101 =10 to move the non-repeating part:

Step #3: Multiply both sides by 102 =100 to shift the Decimal:

Step #4: Subtract the original equation from this new equation:

Step #5: Solve for x:

Final Answer: 61/495

Why it is important to convert Recurring Decimals into Fraction?

  • Converting recurring decimals into fractions is important because recurring decimals are approximations of fractions, but fractions provide an exact representation of the number.

Examples:

  • A recipe might call for 1/3 cup of flour, which is more practical than 0.3333… cups.

  • If a bank offers an interest rate of 0.3333… it’s easier to express it as 1/3 to simplify calculations.

  • In Chemistry, Mole ratios in reactions often involve fractions (e.g., 0.1666… moles = 1/6​ mole).

Three Additional Solved Examples

certified Physics and Maths tutorSolved Example 1

Problem: Convert 0.333… into Fraction.

Solution: 

Step #1: Let x = 0.333…

Step #2: Multiply both side by 10:

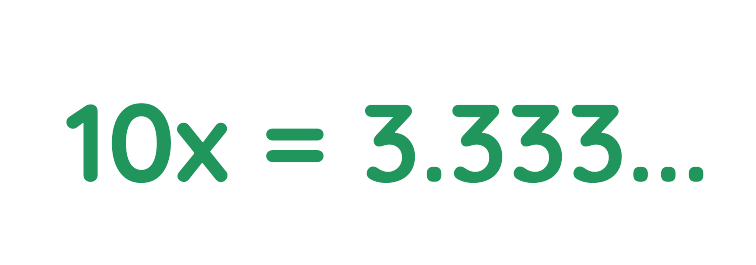
Step #3: Subtract the original equation from this new equation:

Step #4: Solve for x:

Final Answer: 1/3

certified Physics and Maths tutorSolved Example 2

Problem: Convert 0.181818… into Fraction.

Solution: 

Step #1: Let x = 0.1818…

Step #2: Multiply both side by 100:

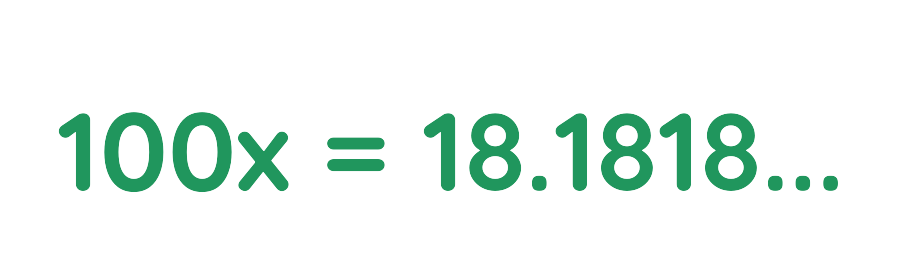
Step #3: Subtract the original equation from this new equation:

Step #4: Solve for x:

Final Answer: 2/11

certified Physics and Maths tutorSolved Example 3

Problem: Convert 0.6333… into Fraction

Solution: 

Step #1: Let x = 0.6333…

Step #2: Multiply both side by 101 =10 to move the non-repeating part:

Step #3: Multiply both sides by 102 =100 to shift the Decimal:

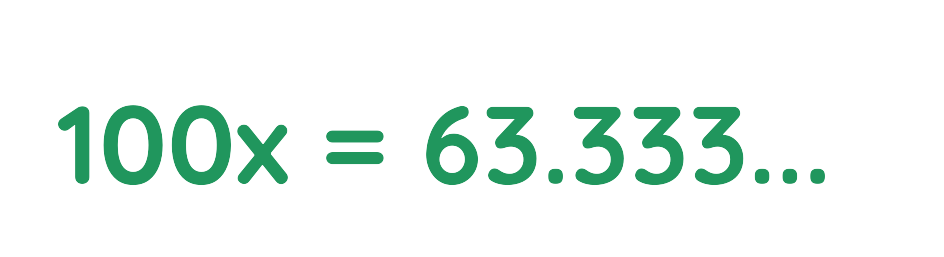
Step #4: Subtract the original equation from this new equation:

Step #5: Solve for x:

Final Answer: 19/30

Practice Questions and Answers on Decimal Recurring to Fraction

Question 1: Convert the Pure Recurring Decimal 0.121212… to a fraction.

Question 2: Convert the Pure Recurring Decimal 0.2222… to a fraction.

Question 3: Convert the Pure Recurring Decimal 0.090909… to a fraction.

Question 4: Convert the Pure Recurring Decimal 0.142142… to a fraction.

Question 5: Convert 0.479479… form of Pure Recurring decimal to a fraction.

Question 6: Convert the Mixed Recurring Decimal 2.333… to a fraction.

Question 7: Converting the Mixed Recurring Decimal 0.10909… to a fraction.

Question 8: Converting the Mixed Recurring Decimal 0.5666… to a fraction.

Question 9: Convert the Mixed Recurring Decimal 2.272727… to a fraction.

Question 10: Convert the Pure Recurring Decimal 0.5555… to a fraction.

Solutions

Question 1: 

Solution: 

Step#1: Let x = 0.1212…

Step#2: Multiply both sides by 100

100x = 12.1212…

Step#3: Subtract the original equation

100x − x = 12.1212… − 0.1212…

99x = 12

Step#4: Solve for x

x = 12 ÷ 99

= 4 ÷ 33

Answer: 4/33

 

Question 2:

Solution: 

Step#1: Let x = 0.2222…

Step#2: Multiply both sides by 10

10x = 2.222…

Step#3: Subtract the original equation

10x − x = 2.222… − 0.222…

9x = 2

Step#4: Solve for x

x = 2 ÷ 9

Answer: 2/9

 

Question 3:

Solution: 

Step#1: Let x = 0.090909…

Step#2: Multiply both sides by 100

100x = 9.0909…

Step#3: Subtract the original equation

100x − x = 9.0909… − 0.0909…

99x = 9

Step#4: Solve for x

x = 9 ÷ 99

= 1 ÷ 11

Answer: 1/11

 

Question 4:

Solution: 

Step#1: Let x = 0.142142…

Step#2: Multiply both sides by 1000

1000x = 142.142142…

Step#3: Subtract the original equation

1000x − x = 142.142142… − 0.142142…

999x = 142

Step#4: Solve for x

x = 142 ÷ 999

Answer: 142/999

 

Question 5: 

Solution: 

Step#1: Let x = 0.479479…

Step#2: Multiply both sides by 1000

1000x = 479.479479…

Step#3: Subtract the original equation

1000x − x = 479.479479… − 0.479479…

999x = 479

Step#4: Solve for x

x = 479 ÷ 999

Answer: 479/999

 

Question 6: 

Solution: 

Step#1: Let x = 2.333…

Step#2: Multiply both sides by 10

10x = 23.333…

Step#3: Subtract the original equation

10x − x = 23.333… − 2.333…

9x = 21

Step#4: Solve for x

x = 21 ÷ 9 = 7 ÷ 3

Answer: 7/3

 

Question 7: 

Solution: 

Step#1: Let x = 0.10909…

Step#2: Multiply both sides by 10

10x = 1.0909…

Step#3: Multiply both sides again by 100

1000x = 109.0909…

Step#4: Subtract

1000x − 10x = 109.0909… − 1.0909…

990x = 108

Step#5: Solve for x

x = 108 ÷ 990

= 6 ÷ 55

Answer: 6/55

 

Question 8: 

Solution: 

Step#1: Let x = 0.5666…

Step#2: Multiply both sides by 10

10x = 5.666…

Step#3: Multiply both sides again by 10

100x = 56.666…

Step#4: Subtract

100x − 10x = 56.666… − 5.666…

90x = 51

Step#5: Solve for x

x = 51 ÷ 90 = 17 ÷ 30

Answer: 17/30

 

Question 9: 

Solution:

Step#1: Let x = 2.2727…

Step#2: Multiply both sides by 100

100x = 227.2727…

Step#3: Subtract

100x − x = 227.2727… − 2.2727…

99x = 225

Step#4: Solve for x

x = 225 ÷ 99 = 25 ÷ 11

Answer: 25/11

 

Question 10: 

Solution: 

Step#1: Let x = 0.555…

Step#2: Multiply both sides by 10

10x = 5.555…

Step#3: Subtract the original equation

10x − x = 5.555… − 0.555…

9x = 5

Step#4: Solve for x

x = 5 ÷ 9

Answer: 5/9

Request for Demo Lesson

Table of Content