Cylinder and Spheres – GCSE Maths

Practice Questions
Downloads

Introduction

  • Cylinders and Spheres are three-dimensional geometric shapes that play essential role in mathematics, architecture, engineering, and everyday life.
  • Both shapes can be described using the radius (r) as a key measurement, but they differ in shape and symmetry.

Real life Examples:

Real-life examples of cylinders and spheres including soda can, batteries, pipes, basketball, planet, and bubbles

What is a Cylinder?

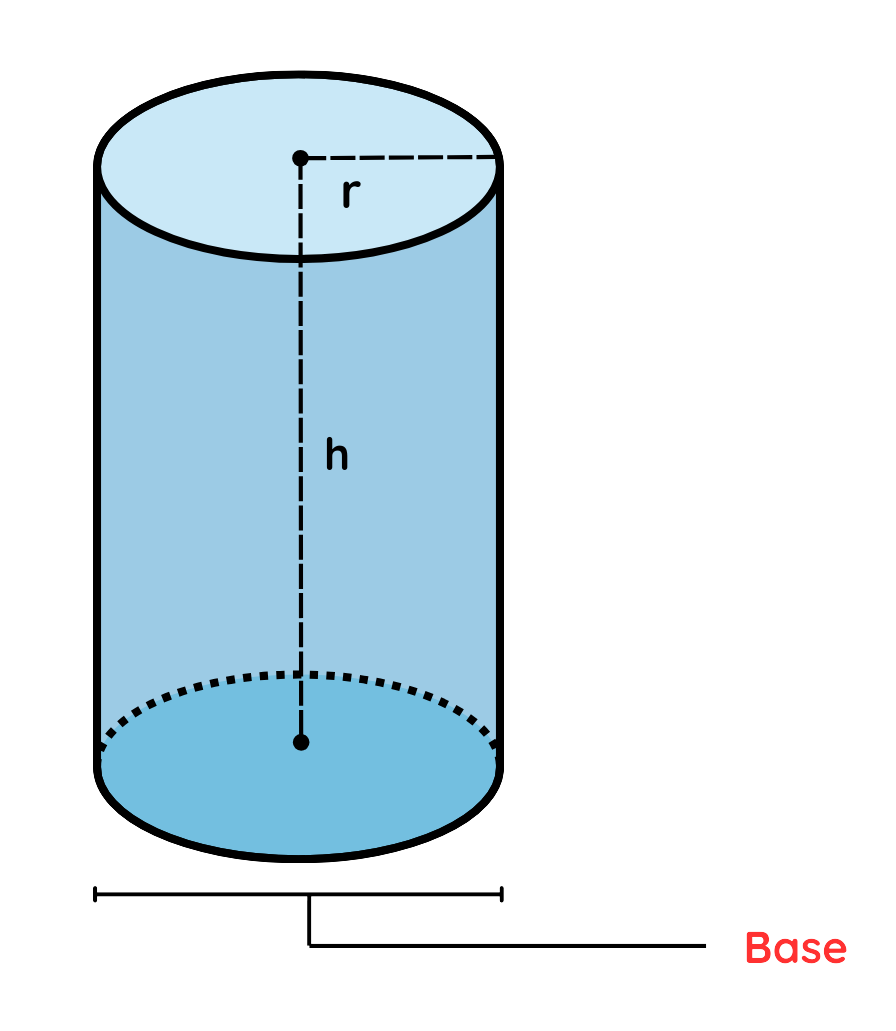
  • A Cylinder is a three-dimensional geometric shape with two parallel circular bases that are congruent (same size and shape).
  • These Bases are connected by a curved surface.

Key Features of a Cylinder:

  • Bases – Two circular and parallel faces.
  • Height (h) – The perpendicular distance between the two bases.
  • Radius (r) – The distance from the center to the edge of the circular base.

A labeled diagram of a cylinder showing radius (r), height (h), and base

What is a Sphere?

  • A Sphere is a perfectly symmetrical three-dimensional shape where Every point on the surface is the same distance from a central point (called the center).
  • It has no edges or vertices

Key Features of a sphare:

  • Radius (r) – The distance from the center to any point on the surface.
  • Diameter (d) – Twice the radius (d=2r).

Diagram of a sphere with labels for radius (r) and diameter (d), showing internal cross-section

How to Find the Volume of Cylinder and Spheres?

  • Volume is the amount of space occupied by an object.

Volume of a Cylinder:

  • The Formula for its volume is:

Formula for calculating the volume of a cylinder: Volume = πr²h

Where,

    • r = radius of the base
    • h = height

Volume of a Sphere:

  • The Formula for its volume is:

Volume formula of a sphere: 4 divided by 3 times pi times radius cubed

Where,

    • r = radius of the base

Steps to Calculate Volume for Cylinder and Sphere:

  • Step#1: Find the radius or height.
  • Step#2: Put the values in formula.
  • Step#3: Compute the Result.

certified Physics and Maths tutorSolved Example

Problem: A cylindrical water tank has a diameter of 14 meters and a height of 5 meters. Calculate its volume. (Use π = 3.14)

A cylindrical water tank with diameter 14 meters and height 5 meters

Solution: 

Step #1: Find the radius:

    • Given diameter (d) = 14 m

Radius equals diameter divided by 2; 14 divided by 2 equals 7 meters

Step #2: Put the values in formula:

Volume formula for a cylinder with radius 7 and height 5: pi times 7 squared times 5

Step #3: Compute the Result:

Volume equals 3.14 times 49 times 5, approximately 769.69 cubic meters

The Volume is 769.69m³

Final Answer: 769.69m³

certified Physics and Maths tutorSolved Example

Problem: A basketball has a diameter of 24 cm. Calculate its volume. (Use π = 3.14)

A basketball with a diameter of 24 cm, used for volume calculation of a sphere

Solution: 

Step #1: Find the radius:

    • Given diameter (d) = 24cm

Radius equals diameter divided by 2; 24 divided by 2 equals 12 cm

Step #2: Put the values in formula:

Volume equals 4 divided by 3 times pi times 12 cubed

Step #3: Compute the Result:

Volume equals four-thirds times 3.14 times 1728, approximately 7238.23 cubic centimetres

The Volume is 7238.23cm³

Final Answer: 7238.23cm³

How to Find the Surface Area of Cylinder and Spheres?

  • Surface area is the Total Area of all the surfaces (faces, bases, and curved sides) that cover a 3D object.

Surface area of a Cylinder:

  • The Formula for its Surface area is:

Surface area equals 2 pi r squared plus 2 pi r h

Where,

    • r = radius of the base
    • h = height

Surface area of a Sphere:

  • The Formula for its Surface area is:

Surface area equals 4 pi r squared

Where,

    • r = radius of the base

Steps to Calculate Surface Area for Cylinder and Spheres:

  • Step#1: Find the radius or height.
  • Step#2: Put the values in formula.
  • Step#3: Compute the Result.

certified Physics and Maths tutorSolved Example

Problem: A pipe has a radius of 5 cm, and a height of 12 cm. Find its total surface area. (Use π = 3.14)

Cylinder with height 12 cm and radius 5 cm

Solution: 

Step #1: Find the radius:

Radius of a cylinder is 5 centimeters

Step #2: Put the values in formula:

Surface area formula for a cylinder with substituted values for radius 5 cm and height 12 cm

Step #3: Compute the Result:

Final step in calculating the surface area of a cylinder using radius 5 cm and height 12 cm, showing 170π and 534.07 cm²

The Surface Area is 534.07 cm2

Final Answer: 534.07 cm2

certified Physics and Maths tutorSolved Example

Problem: A globe has a diameter of 30 cm. Find its surface area. (Use π = 3.14)

Diagram of a purple sphere with a 30 cm diameter marked across the center

Solution: 

Step #1: Find the radius:

    • Given diameter (d) = 30cm

Formula showing radius equals diameter divided by 2, with 30 ÷ 2 = 15 cm

Step #2: Put the values in formula:

Surface area formula for a sphere with 15 cm radius shown as 4πr² = 4π(15)²

Step #3: Compute the Result:

Final calculation of surface area for a sphere using 4π × 225 = 900 × 3.14 ≈ 2827.43 cm²

The Surface Area is 2827.43 cm2

Final Answer: 2827.43 cm2

Table of Content

Join Tutoring