Completing the Square: Comprehensive Guide With Worksheet

Calculator
Test Youself

Completing the Square

What is Completing the Squares?

  • Completing the squares is a powerful technique used in algebra to solve quadratic equations.

In this article, we will discuss: 

  1. What is Completing the Squares?
  2. What are the different applications of Completing the Squares?
  3. GCSE Past Paper Questions

Here is one more link to practice a few extra questions: Maths Genie Completing the Squares Questions

What is Completing the Square used for?

  • Completing the Square involves converting any quadratic equation of the type:

ax2 + bx + c  —->  a(x-h)2 + k

It can be used to:

  1. Find the Turning Point of a Quadratic Equation
  2. Find the Maximum or Minimum value of a Quadratic Equation
  3. Solve a quadratic equation and find its roots

Turning Point from Completing the Square

What is the Turning Point of a Quadratic Equation?

  • The graph of quadratic equation represents a parabola, which can look something like this: curving either upward or downward

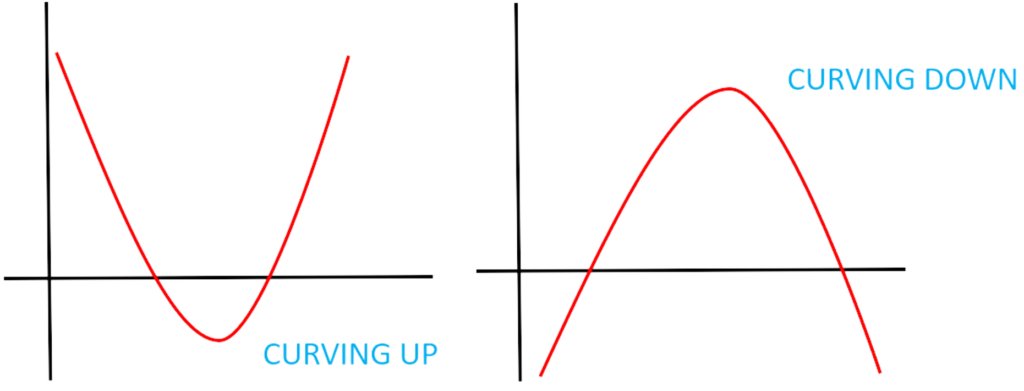
Graph showing the turning points of a quadratic equation, with parabolas curving upward and downward.

Our goal is to locate the turning point of this parabola.

To illustrate the process, let’s work through a straightforward example:

certified Physics and Maths tutor

 

 

Solved Example

Question: Find the Turning Point of the Quadratic Equation x2 + 3x – 10

Solution:

  • Step #1: Begin with a quadratic equation in standard form, ax2 + bx + c.

For our example, a = 1, b = 3, and c = -10.

  • Step #2: Apply Completing the Square to transform it into vertex form.

1. First, factor out the leading coefficient ‘a’ from the first two terms:

x2 + 3x – 10 = 1(x2 + 3x) – 10

2. To complete the square, we need to add and subtract (b/2)2 inside the

     parentheses. In this case,

(3/2)2 = 9/4. x2 + 3x + 9/4 – 10 – 9/4

3. Rearrange the equation by grouping the terms:

(x2 + 3x + 9/4) – (40/4 + 9/4)

4. Simplify both sides:

(x + 3/2)2 – 49/4

  • Step #3: Rewrite it in vertex form, a(x-h)2 + k.

In our example, a = 1, h = -3/2 (opposite sign), and k = 49/4.

So, the turning point of the quadratic equation x2 + 3x – 10 is (-3/2, 49/4).

Practice Questions

Question 1. Find the turning point of the quadratic equation: x2− 6x + 9

Answer : ( , )


Question 2: Determine the turning point of the quadratic equation: x2 + 4x − 4

Answer : ( , )

Exploring Completing the Square with 'a' Not Equal to 1

What happens when the coefficient of x2 is not 1?

  • Up until now, we’ve worked with quadratic equations where ‘a’ (the coefficient of x2) was conveniently set to 1.

This simplified the Completing the Square process.

However, quadratic equations in real-world scenarios often have ‘a’ values other than 1.

Let’s tackle a more complex example:

certified Physics and Maths tutor     Challenging Example Question: Find the Turning Point of 2x2 – 8x – 5 Solution:
  • Step #1: Begin with the given quadratic equation:

2x2 – 8x – 5

  • Step #2: To complete the square, factor out the leading coefficient ‘a’ (which is 2 in this case) from the first two terms:

2(x2 – 4x) – 5

  • Step #3: Now, we need to add and subtract (b/2)2 inside the parentheses. Here, (4/2)2=4, so we add and subtract 4:

2(x2 – 4x + 4 – 4) – 5

  • Step #4: Rearrange the equation by grouping the terms:

2((x2 – 4x + 4) – 4) – 5

  • Step #5: Simplify the grouped terms inside the parentheses:

2((x – 2)2 – 4) – 5

  • Step #6: Distribute the 2 back into the expression:

2(x – 2)2 – 8 – 5

  • Step #7: Simplify further:

2(x – 2)2 – 13

Now, we have successfully completed the square, and the equation is in vertex form, a(x – h)2 + k, where a = 2, h = 2, and k = -13

So, the turning point of the quadratic equation 2x2 – 8x – 5 is (2, -13).

Practice Questions

Question 1. Find the turning point of the quadratic equation: 3x2 − 12x + 10

Answer : ( , )


Question 2: Determine the turning point of the quadratic equation: -2x2 + 8x - 6

Answer : ( , )

Finding Maxima and Minima from Completing the Square

How to find the Maximina and Minima of a Quadratic Equation?

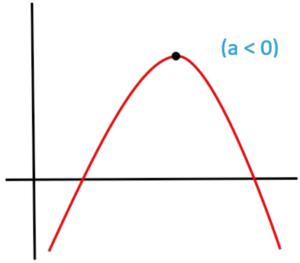
  • The concept of maximum and minimum values in the quadratic function represents the highest and lowest points on the parabolic graph formed by the quadratic equation.
  • Maximum values occur when the parabola opens downward (a < 0),

Parabola Opens Downward (Completing the Square)

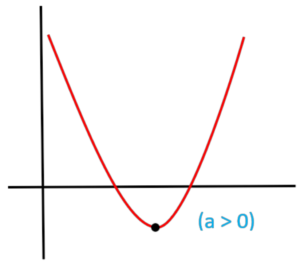
  • Minimum values occur when it opens upward (a > 0).

Parabola Opens Upward (Completing the Square)

certified Physics and Maths tutor

 

 

Solved Example

Question: Find the Maximum or Minimum Value of the Quadratic Equation 2x2 – 8x + 6

Solution:

  • Step #1: Begin with the given quadratic equation:

2x2 – 8x + 6

  • Step #2: Factor out the leading coefficient ‘a’ (which is 2 in this case) from the first two terms:

2(x2 – 4x) + 6

  • Step #3: Add and subtract (b/2)2 inside the parentheses. Here, (4/2)2 = 4, so we add and subtract 4:

2(x2 – 4x + 4 – 4) + 6

  • Step #4: Rearrange the equation by grouping the terms:

2((x2 – 4x + 4) – 4) + 6

  • Step #5: Simplify the grouped terms inside the parentheses:

2(x – 2)2 – 8 + 6

  • Step #6: Distribute the 2 back into the expression:

2(x – 2)2 – 2

Now, we have it in vertex form, a(x – h)2 + k, where a = 2, h = 2, and k = -2.

In this case, ‘a’ is positive (a > 0), indicating that the parabola opens upward. Therefore, the vertex represents the minimum value.

So, the minimum value of the quadratic equation 2x2 – 8x + 6 is -2, and it occurs at the vertex, which is (2, -2).

Practice Questions

Question 1. Find the maximum or minimum value of the quadratic equation: x2 + 6x + 9

Answer :


Question 2: Determine the maximum or minimum value of the quadratic equation: -3x2 - 12x - 15

Answer :

Solving Quadratic Equations

  • Completing the squares can also be used to find the roots of a quadratic equation.
  • Other techniques that can be used is factorisation and quadratic formula.
  • To illustrate how Completing the Square can be used for solving quadratic equations, let’s work through an example:

certified Physics and Maths tutor

 

 

Solved Example

Question: Solve the Quadratic Equation x2 – 6x + 9 = 0

Solution:

  • Step #1: Begin with the given quadratic equation:

x2 – 6x + 9 = 0

  • Step #2: Express it in standard form, with one side equal to zero:

x2 – 6x + 9 – 9 = 0 – 9

  • Step #3: Factor out the leading coefficient ‘a’ (which is 1 in this case) from the first two terms:

(x2 – 6x) + 9 – 9 = -9

  • Step #4: Add and subtract (b/2)2 inside the parentheses. Here, (6/2)2 = 9, so we add and subtract 9:

(x2 – 6x + 9 – 9) = -9

  • Step #5: Rearrange the equation by grouping the terms:

     

(x2 – 6x + 9) – 9 = -9

  • Step #6: Simplify the grouped terms inside the parentheses:

(x – 3)2 – 9 = -9

  • Step #7: Add 9 to both sides to isolate the perfect square:

(x – 3)2 = 0

  • Step #8: Take the square root of both sides:

x – 3 = ±√0

  • Step #9: Simplify the square root of 0 to 0:

x – 3 = ±0

  • Step #10: Solve for ‘x’ by adding 3 to both sides:

x = 3

 So, the solution to the quadratic equation x2 – 6x + 9 = 0 is x = 3.

Practice Questions

Question 1. Solve the quadratic equation: 2x2 + 4x - 6 = 0

Answer : ( , )


Question 2: Find the solutions to the quadratic equation: x2 + 8x + 16 = 0

Answer : ( , )

Completing the Square GCSE questions

certified Physics and Maths tutor

 

 

GCSE Past Paper Question 1: Finding the Turning Point

Question: Find the coordinates of the turning point on the curve with the equation

y = 9 + 18x – 3x2. Show all your working.

Solution:

  • Step #1: Begin with the given equation:

y = 9 + 18x – 3x2

  • Step #2: Express it in standard form by rearranging the terms:

y = -3x2 + 18x + 9

  • Step #3: Factor out the leading coefficient ‘a’ (which is -3 in this case) from the first two terms:

y = -3(x2 – 6x) + 9

  • Step #4: Complete the square by adding and subtracting (b/2)2 inside the parentheses. Here, (6/2)2 = 9:

y = -3(x2 – 6x + 9 – 9) + 9

  • Step #5: Rearrange the equation by grouping the terms:

y = -3((x2 – 6x + 9) – 9) + 9

  • Step #6: Simplify the grouped terms inside the parentheses:

y = -3(x – 3)2 – 27 + 9

  • Step #7: Further simplify:

y = -3(x – 3)2 – 18

Now, we have the equation in vertex form, a(x – h)2 + k, where a = -3, h = 3,

and k = -18.

The turning point’s coordinates are (h, k) = (3, -18).

So, the coordinates of the turning point on the curve with the equation

y = 9 + 18x – 3x2 are (3, -18).

Request for Demo Lesson

certified Physics and Maths tutor

 

 

GCSE Past Paper Question 2: Sketching the Graph

Question: Sketch the graph of y = 2x2 – 8x – 5, indicating the turning point and providing the precise coordinates of any intercepts with the coordinate axes.

Solution: 

To sketch the graph of the given equation, let’s first identify the key elements:

the turning point and the intercepts.

Turning Point:

We’ve already found the turning point coordinates in a previous example:

(h, k) = (2, -9).

Intercepts:

To find the intercepts, we set y = 0 and solve for ‘x’ (x-intercepts) or set x = 0

and solve for ‘y’ (y-intercepts).

For x-intercepts (when y = 0):

0 = 2x2 – 8x – 5

We can use the quadratic formula to find the roots:

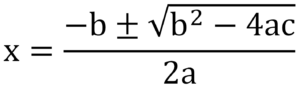
Quadratic formula equation showing the solution for x in terms of coefficients a, b, and c.

In this case, a=2, b=−8, and c=−5.

Calculating the roots, we get:

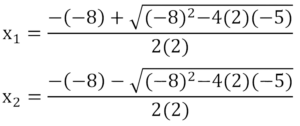
Quadratic equation with solved x-intercepts using the quadratic formula.

Solving these, we find the x-intercepts:

x1 ≈ −0.68 (rounded to two decimal places)

x2 ≈ 3.18 (rounded to two decimal places)

For y-intercepts (when x = 0):

y = 2(0)2 – 8(0) – 5

y = -5

So, the y-intercept is at (0, -5).

Now, we can sketch the graph with these key elements:

  • Turning Point: (2, -9)
  • X-Intercepts: (-0.68, 0) and (3.18, 0)
  • Y-Intercept: (0, -5)

Plot these points and sketch the parabolic curve. The graph of y = 2x2 – 8x – 5 should resemble a parabola opening upward with the specified features.

Worksheet on Completing the Squares

Question 1: Turning Point: Find the coordinates of the turning point on the curve with the equation:
y = 4 - 8x + 3x2 

)

Question 2: Completing the Square: Convert the following quadratic equation into vertex form (a(x - h)2 + k) by completing the square: y = x2 - 6x + 9



Question 3: Solving Quadratic Equations: Solve the quadratic equation: x2 + 5x - 6 = 0

)

Question 4: Graph Sketching: Sketch the graph of the quadratic equation y = -x2 + 4x + 3 and label the coordinates of the turning point and any intercepts with the coordinate axes.

)

Question 5: Solving Quadratic Equations: Solve the quadratic equation: 2x2 - 12x + 18 = 0