Turning Point Quadratic Equation Calculator

Ever the values of “a” , “b” & “c” for the general quadratic equation ax2 + bx + c. The Calculator will give you the values of the Turning Point and Roots of the Quadratic Equation

Quadratic Equation Calculator



Turning Point of a Quadratic Equation

What is Turning Point of Quadratic Equation?

  • The turning point of a quadratic equation, also known as the vertex, is the point on the graph of the quadratic function where the graph changes direction. 
  • This point represents either the maximum or minimum value of the quadratic function, depending on the direction in which the parabola opens.
 

For a quadratic equation in the form

y=ax2+bx+c

, the turning point can be found using the formula:

where a, b, and c are constants, and x represents the variable. Quadratic equations often depict parabolic curves when graphed, showcasing a symmetrical arc that either opens upwards or downwards.

x=−b2a

  • The x-coordinate of the turning point,
    −b2a

     

    , is the axis of symmetry for the parabola.

  • The y-coordinate,
    f(−b2a)

     

    , represents the maximum or minimum value of the quadratic function.

  1. If ‘a’ is positive, the parabola opens upward, and the turning point is the minimum.
  2. If ‘a’ is negative, the parabola opens downward, and the turning point is the maximum.
  • The graph of quadratic equation represents a parabola, which can look something like this: curving either upward or downward

Completing the Square (Turning points)

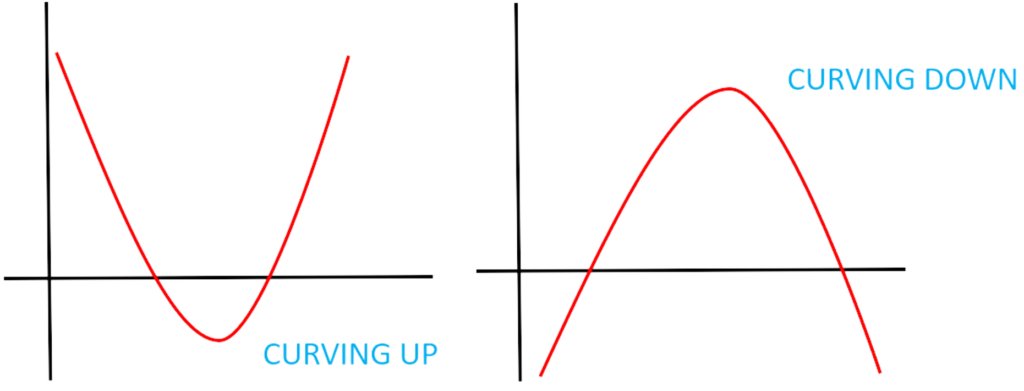
Our goal is to locate the turning point of this parabola.

  • if your coefficient “a > 0”, then it represents the lowest point on the parabola, and if your coefficient “a < 0”, it represents the highest point of the parabola.

Thus we can say:

The turning point is a crucial concept when analyzing and graphing quadratic equations, as it provides information about the highest or lowest point on the parabolic curve.