Steps to Calculate The Bearing of an Angle? GCSE Maths
Wondering how to calculate the bearing of Y from X in your GCSE Maths problems? Let’s break it down step by step and make it simple.
Video Tutorial on Bearings
Watch this Video Tutorial as we explain step by step how to calculate the Bearing of Y from X
What Are Bearings?
- So, what exactly is a bearing?
- Think of a bearing as a way to describe direction—kind of like giving someone precise instructions on which way to go.
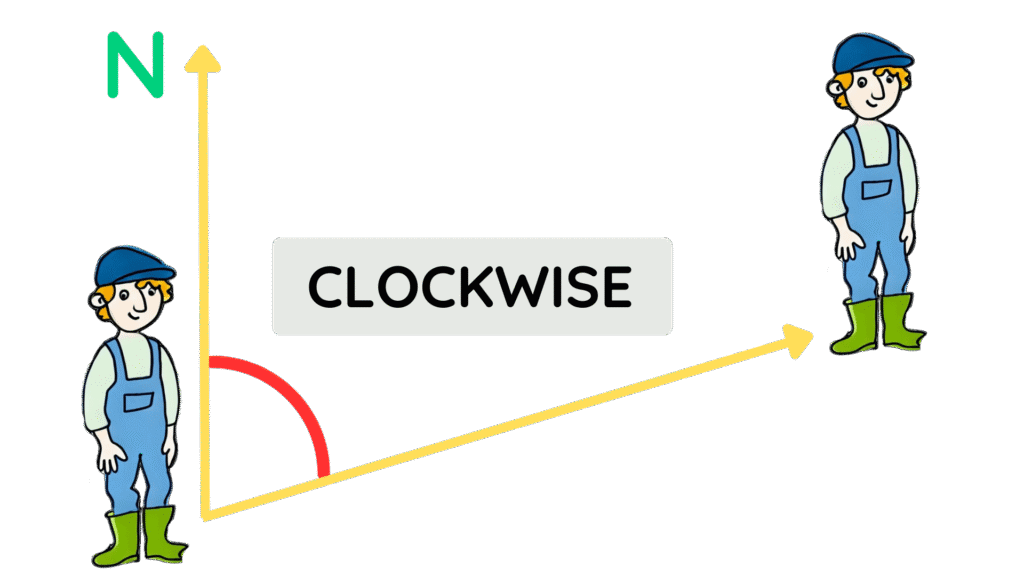
- In maths, a bearing is an angle measured clockwise from the north direction.
- Bearings are especially useful in navigation and mapping because they provide an exact angle between two points.

So when we talk about calculating the bearing of Y from X, we’re figuring out the direction you need to face at point X to look straight towards point Y.
Here is one more link to practice a few extra questions: Maths Genie Bearings Questions
Things to Remember When Calculating the Bearing of Y from X
When calculating a bearing, there are a three important things to remember.
- Always Measure Clockwise from North: Bearings are measured starting from the north direction and moving clockwise. Think of a compass where the north is at the top, and you turn in the direction the clock’s hands move.


- This three-digit system helps to avoid any confusion and makes everything very clear.
3. Know the Cardinal Points: Familiarize yourself with the basic compass points:
- North (N) is 000° or 360°
- East (E) is 090°
- South (S) is 180°
- West (W) is 270°
Steps to Calculate The Bearing of Y From X
- How to calculate the bearing of Y from X? Let’s walk through the steps together:
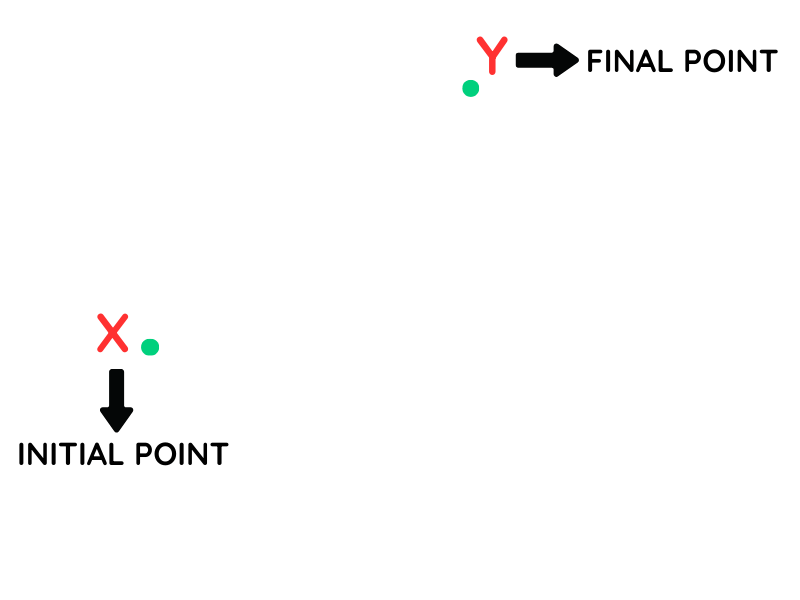
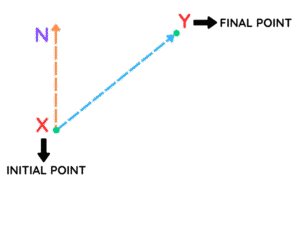
Figure out the Inital point and the Final point: For example, since we need to find the bearing of Y “FROM” X. This “From” tells us that X is our initial point and Y is our final point.
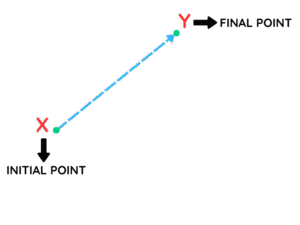
- Draw the Line from X to Y
Connect point X to point Y with a straight line. This line shows the direct path from X to Y. You can also add an arrow to indicate the direction.
2. Mark the North Direction at Point X: At point X, draw a vertical line pointing upwards to represent the north direction. This is crucial because bearings are always measured clockwise from north.
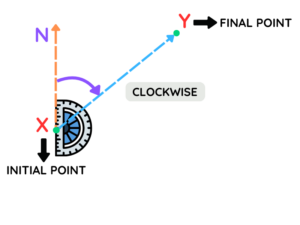
Measure the Angle Clockwise from North to the Line XY
Using a protractor, measure the angle starting from the north line at point X and moving clockwise until you reach the line connecting X to Y. This angle is your bearing.
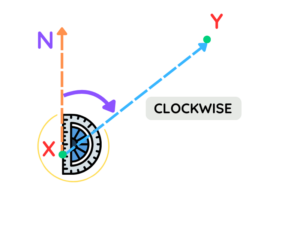
- One important thing to remember is that you will always measure the clockwise angle from the north direction.
- Since this is the north, we will draw a clockwise angle like this. Always remember to go clockwise—you will not use the angle that goes in the anticlockwise direction.
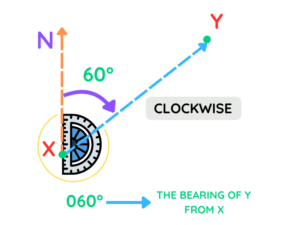
Express the Bearing as a Three-Digit Number
Bearings are written as three-digit numbers. If your angle is less than 100 degrees, add leading zeros to make it three digits. For example:
- If the angle is 60°, write the bearing as 060°.
- If it’s 120°, the bearing remains 120°.
Double-Check Your Measurement
It’s easy to make a mistake with angles, so take a moment to verify your measurement and ensure your protractor was aligned correctly.
Solved Example:
Question: By measuring the angles below, state the bearings of
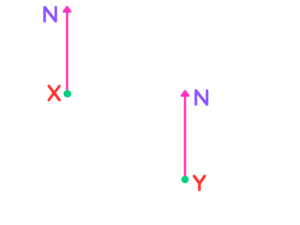
X From Y.
Solution:
Let’s start by finding the bearing of X from Y. This means our initial point is Y and our final point is X.
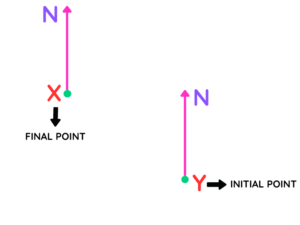
- Step #1: Draw a line from our initial point to our final or destination point. From the initial point, that is Y, we will measure the angle in a clockwise direction.
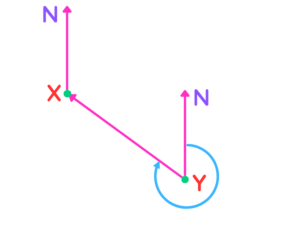
- Step #2: Now, measuring this angle can be a bit tricky sometimes, so you can start by measuring the smaller interior angle. Let’s say this angle is 40 degrees.
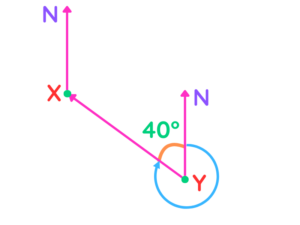
- Step #3: To find the bearing, that is the larger blue angle, we can subtract 40 from 360 to get 320 degrees.

Therefore, the bearing of X from Y is 320 degrees.
Solved Example:
Question: By measuring the angles below, state the bearings of

Y From X.
Solution:
Step #1: This means our initial point is X and our final point is Y. This time, the direction of the line is from X to Y, not Y to X.
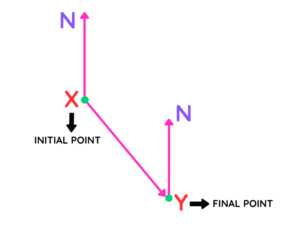
Step #2: We draw the angle in the clockwise direction from X. This gives us the bearing of Y from X, which comes out to be 140 degrees.

- There are actually two methods to solve this part.
- The first is to use a protractor to measure the angle, as we did earlier.
- Alternatively, you can use the property of parallel lines that states the sum of the interior angles between two parallel lines is 180 degrees. This property can sometimes make finding the bearing quicker.
Exam Practice Questions:
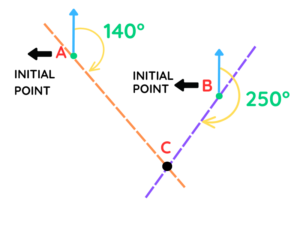
Question 1: The location C is on a bearing of 140° from A.
The bearing of C from B is 250°
Find the location C and mark it on the diagram below.

Solution:
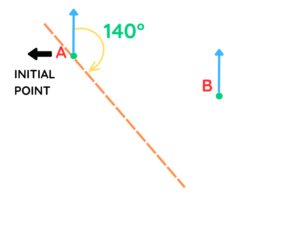
- Step #1: This question is divided into two parts, and we need to determine the location of C. We are given the bearings of C from both “A” and B, and we need to draw these bearings one by one.
- Step #2: We are told that the location of C is on a bearing of 140 degrees from A. So, we take A as our initial point and draw a line at a bearing of 140 degrees from A. Using a protractor, we measure 140 degrees and then draw a dashed line in that direction. C could be located anywhere along this dashed line.
- Step #3: Next, we need to find the bearing of C from B. Again, we take point B as our initial point and draw a 250-degree angle in a clockwise direction. We draw another dashed line from this point. The intersection of these two lines gives us the location of C.
Practice Questions and Answers on Bearings
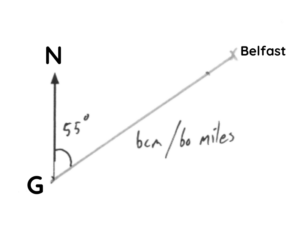
Question 1: The diagram shows the position of Glasgow.

Belfast is 60 miles away from Glasgow on a bearing of 055°
Mark the position of Belfast on the diagram.
Question 2: A diagram of a bearing is shown below.
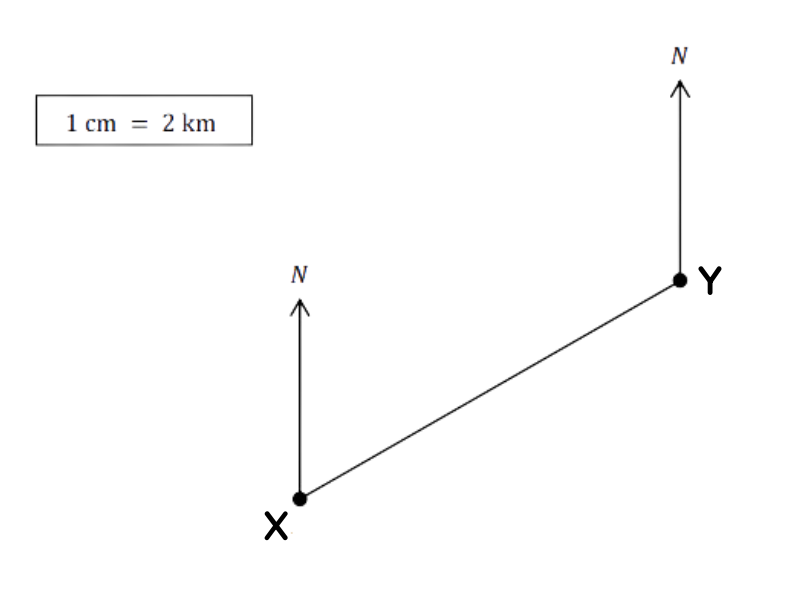
By measuring the diagram given:
(a) State the bearing of Y from X.
(b) State the bearing of X from Y
(c) Find the distance between X and Y.
Question 3:
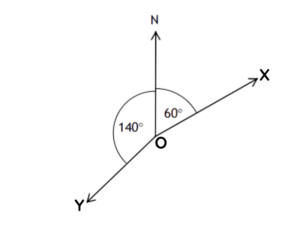
(a) Write down the bearing of X from O.
(b) Work out the bearing of Y from O.
Question 4: Mark has been asked to find the bearing of X from Y.
Shown below is her method.
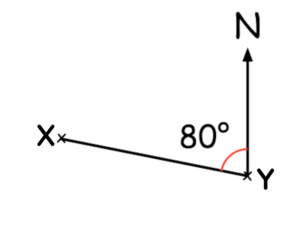
Mark answer is 080°
Explain Mark mistake.
Question 5: Starting at point E, Jacob makes a journey as follows:
8 km on a bearing of 135° to F
4 km, on a bearing of 180° to G
6 km on a bearing of 315° to H
(a) Use the space below to draw a suitable diagram to represent her journey.

(b) Jacob wants to return to E.
What is the bearing of E from H?
Question 6:
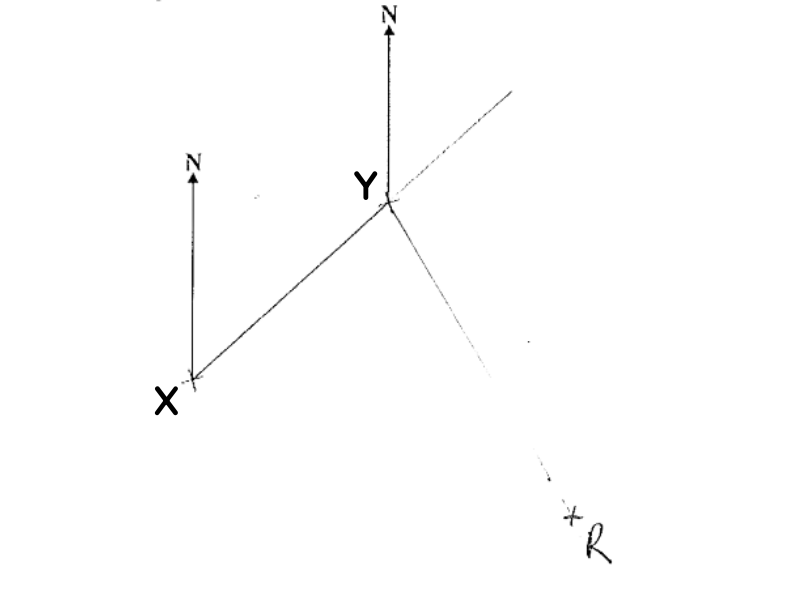
The diagram shows the position of two ports X and Y on a map.
(a) Measure the bearing of Y from X.
A rock R is on a bearing of 150° from Y.
On the map R is 6 cm from Y.
(b) Mark the position of R with a cross (×) and label it R.
Question 7: Alex has been asked to find the bearing of X from Y.
Shown below is his method.

Alex answer is 103°
Explain Alex mistake.
Question 8:
The diagram shows the position of a lighthouse X and a harbour Y.
The scale of the diagram is 1 cm represents 5 km.
(a) Work out the real distance between X and Y.
(b) Measure the bearing of Y from X.
A boat B is 20 km from Y on a bearing of 040°
(c) On the diagram, mark the position of boat B with a cross (×).
Label it B.
Question 9: The diagram shows the position of two boats, A and B.
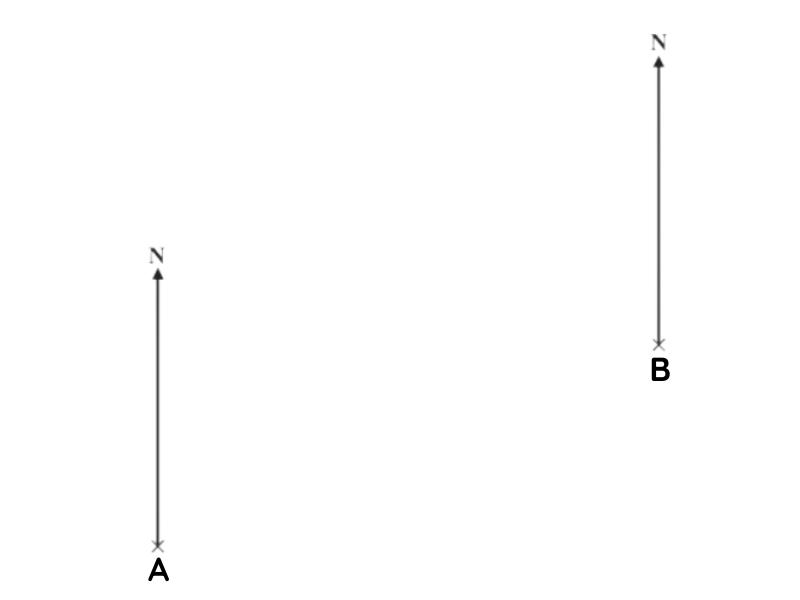
The bearing of a boat C from boat A is 060°
The bearing of boat C from boat B is 310°
In the space above, draw an accurate diagram to show the position of boat C.
Mark the position of boat C with a cross (x). Label it C.
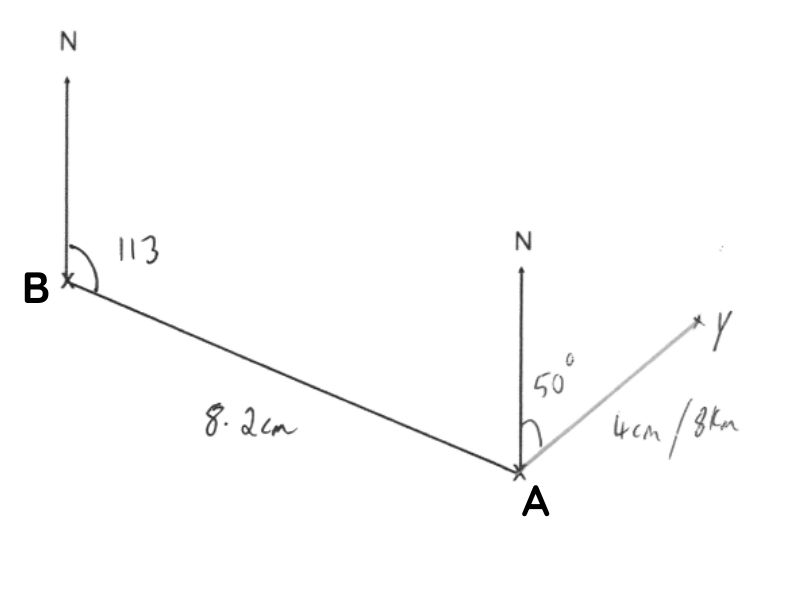
Question 10: The diagram shows the position of a boat A and a dock B.
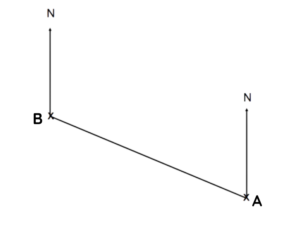
The scale of the diagram is 1cm represents 2km.
(a) Work out the actual distance between the dock and the boat.
(b) Measure the bearing of the boat A from the dock B.
A yash Y is 8km from the boat A on a bearing of 050°
(c) On the diagram, mark the position of yash Y with a cross (x).
Label it Y.
Solutions
Question 1:
Question 2:
(a) 060°
(b) 240°
(c) 12 km
Question 3:
(a) 060°
(b) 220°
Question 4:
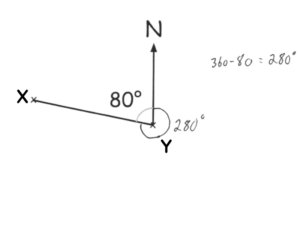
Mark has measured the anticlockwise angle.
The correct answer is 280 degrees
Question 5:
(a)
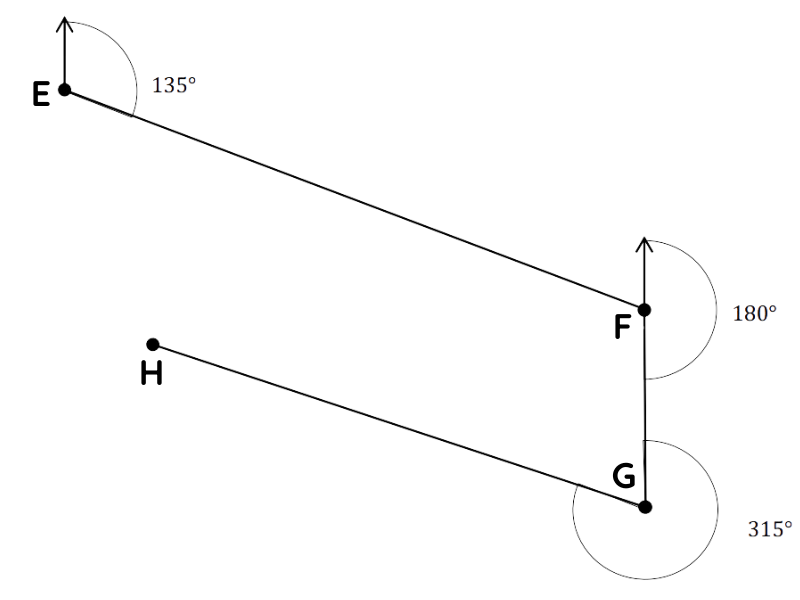
(b) 345° ± 5°
Question 6:
(a) 048°
(b)
Question 7:
Alex has measured the bewig of Y from X, Not X form Y.
The answer would be 283 degrees
Question 8:
(a) 34 km
(b) 110°
(c)

Question 9:

Question 10:
(a) 16.4 km
(b) 113 degrees
(c)