Algebraic Proof: Questions, Examples with Worksheet

Calculator
Test Youself

Algebraic Proof

  • Mathematics submits for a formal proof as a rational argument to make mathematical statements true.
  • Algebraic proofs is a kind of mathematical proof which is mostly used as a tool to prove reach statement with the help of algebraic techniques and manipulations.
In this article, we will discuss: 
  1. What is Algebraic Proof?
  2. What is Geometric Proof?
  3. How to Prove Algebraically?
Here is one more link to practice a few extra questions: Corbettmaths Algebraic Proof Questions

What is Algebraic proof?

  • Proof of the algebraic type is a way of proving the truth of a mathematical judgment with the help of algebraic operations.

  • It makes use of algebraic equations and expressions to substantiate the validity of the assertion which is why it is among the basic tools for proving theorems, identities and equations, to mention a few.

  • Interpretation of an algebraic proof commences with provided data and utilizes algebraic operations to achieve a valid generalization.

certified Physics and Maths tutor

 

 

Solved Example

Question: Prove that for any real number x, x2 – 3x + 2 = 0 if and only if x = 1 or x = 2.

Solution: 

  • Step #1: To prove this statement algebraically, we can start by factoring 

the quadratic equation x2 – 3x + 2 to get (x – 2)(x – 1) = 0.

  • Step #2: Now, using the zero product property, we know that the only way for the product of two factors to equal zero is if one or both of the factors equals zero. Therefore, we have two cases to consider:

(1) x – 2 = 0

or

(2) x – 1 = 0.

  • Step #3: Solving for x in each case, we get x = 2 or x = 1, respectively.
  • Step #4: Conversely, if x = 1 or x = 2, then plugging those values into the original equation yields

(1)2 – 3(1) + 2 = 0 and (2)2 – 3(2) + 2 = 0, respectively.

Thus, we have proven that for any real number x, x2 – 3x + 2 = 0 if and only if x = 1 or x = 2, using algebraic proof techniques such as factoring and the zero product property.

What is Geometric Proof?

  • Geometric proof is another method for the proving of mathematical theorems.
  • It uses the geometry of figures and their properties and takes the truth of the given statement as a basis.
  • Using a geometrical proof for proving various theorems is prominent among geometricians in the field of geometry and trigonometry.
  • The act of a geometric proof usually starts with making a figure describing statement and only then properties of the figure are used to find more information out of which a conclusion is established.

certified Physics and Maths tutor

 

 

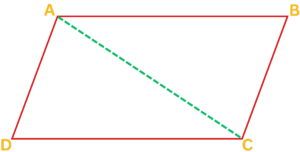
Solved Example: Geometric Proof

  1. Draw a parallelogram ABCD.
  2. Construct the diagonal AC of the parallelogram.
  3. By definition, a parallelogram has two pairs of parallel sides. Therefore, we know that AB || CD and BC || AD.
  4. When a diagonal is drawn in a parallelogram, it creates two congruent triangles (triangle ABC and triangle ADC).
  5. Since these triangles are congruent, their corresponding sides are also congruent.
  6. Therefore, we can conclude that AB = CD and BC = AD, proving that the opposite sides of a parallelogram are congruent.

Algebraic Proof ABCD is a parallelogram

How to Prove Algebraically

  • To make an algebraic proof, we have to start from the given facts, apply different algebraic operations until and we get the conclusion we desire.

Common Algebraic Techniques in Proofs:

1. Simplifying Expressions:

  • The process of simplifying expressions includes combining similar terms, factoring, or expanding them.
  • We recognize the dependences and the functionality of terms the latter makes the processes a lot easier.

2. Substitution:

  • Substitution means the substitution of one variable or expression for another one to simplify an equation.
  • It works as a factor unlike other variables whose effect is being determined.

3. Rearranging Equations:

  • Manipulation of equations is a technique of transforming some equation in a way such that all the variables are separated or an other variable(s) become a function of a specific variable.
  • Thanks to this method of approach the important relations between different factors and complexities of the decision production process are revealed.

4. Using Algebraic Properties:

  • Algebraic properties of the type which are the distributive property, associative property, and the commutative property can be used to simplify expressions and equations together.
  • These properties helped to simplify and solve equations with more ease.

Conclusion

  • Algorithmic form of proof is a powerful utility for stating the truths of mathematical statements as a rule.
  • Algebra provides us with tools like simplifying expressions, substitutions, back-and-forth operations, and applying algebraic identity properties to transform given information involving numbers or variables to fit our purpose and arrive at a well-grounded conclusion.
  • The geometrical proof shows that the proof involves by using geometric figures together with properties that we are going to prove a statement.
  • Through the knowledge and ability to utilize both kinds of justification, people can sharpen their mathematical skills and therefore, become more competent in solving numerical problems.

Practice Questions

Question 1: Demonstrating that the squares of two consecutive odd integers always remain an even number.

Question 2: The sum of any two consecutive even integers is always divisible by 4. Support your answer algebraically.

Question 3: Prove that the product of any two consecutive positive integers is always odd.

Question 4: Show that the sum of cubes of any three consecutive integers is necessary just to be divisible by 3.

Question 5: Solve the problem which is proving that sum of squares of any three odd numbers in a row will always be divisible by 21.

Question 6: Demonstrate that for the properties of the difference between the cubes of any two consecutive integers one obtains always an odd integer.

Question 7: Show that finding the sum of the squares of every two consecutive odd integers, the resultant will always be an even integer.

Question 8: Illustrate that the item of any two consecutive odd integers is always odd.

Question 9: Show that the product of three consecutive even numbers are always divisible by 16.

Question 10: Show that the difference of the squares of any two consecutive odd integers is always a multiple of 8.

Solutions:

Question 1: Demonstrating that the squares of two consecutive odd integers always remain an even number.

Solution:

Step #1: Assumptions and Setup

    • Let´s consider the two odd numbers that succeed in each other equal to 2n+1 and 2n+3.
    • This difference corresponds to the expression (2n+3)2 – (2n+1)2.

Step #2: Application of Algebraic Identity

    • We can simplify this expression using the identity a2 – b2 = (a+b)(a-b):

(2n+3)2 – (2n+1)2 = [(2n+3)+(2n+1)][(2n+3)-(2n+1)]

= (4n+4)(2)

= 8(n+1)

Step #3: Conclusion

    • Since 8 is even, we have proved that the difference between the squares of two consecutive odd integers is always an even number.

Question 2: The sum of any two consecutive even integers is always divisible by 4. Support your answer algebraically.

Solution:

Step #1: Assumptions and Setup

    • Let us consider, 2n and 2n+2 are the two successive even integers.
    • The sum of the terms results in 4n + 2.

Step #2: Factorization

    • After factoring out 2 from the sum, we get 2(2n+1), which is the complete outcome.

Step #3: Divisibility by 4

    • Since 2n+1 is an integer, 2(2n+1) should be always divisible by 4.

Question 3: Prove that the product of any two consecutive positive integers is always odd.

Solution:

Step #1: Assumptions and Setup

    • Let’s assume the two consecutive positive integers are n and n+1.
    • Their product is n(n+1) = n2 + n.

Step #2: Parity Analysis

    • If n is even, then n2 is even and n is even, so their sum n2+ n is even.
    • If n is odd, then n2 is odd and n is even, so their sum n2 + n is odd.
    • Therefore, the product of any two consecutive positive integers is always odd.

Question 4: Show that the sum of cubes of any three consecutive integers is necessary just to be divisible by 3.

Solution:

Step #1: Assumptions and Setup

    • Let’s assume the three consecutive integers are n, n+1, and n+2.
    • The sum of their cubes is n3 + (n+1)3 + (n+2)3.

Step #2: Expression Expansion

    • Expanding this expression, we get:

n3 + (n+1)3 + (n+2)3 = 3n3 + 9n2 + 15n + 9.

Step #3: Factorization

    • We can factor out a 3 from this expression to get:

3n3 + 9n2 + 15n + 9 = 3(n3 + 3n2 + 5n + 3).

Step #4: Divisibility by 3

    • Since n3 + 3n2 + 5n + 3 is an integer, we have shown that the sum of the cubes of any three consecutive integers is always divisible by 3.
Request for Demo Lesson

Question 5: Solve the problem which is proving that sum of squares of any three odd numbers in a row will always be divisible by 21.

Solution:

Step #1: Assumptions and Setup

    • Let’s assume the three consecutive odd integers are 2n+1, 2n+3, and 2n+5.
    • The sum of their squares is (2n+1)2 + (2n+3)2 + (2n+5)2.

Step #2: Expression Expansion

    • Expanding this expression, we get:

(2n+1)2 + (2n+3)2 + (2n+5)2 = 12n2 + 36n + 35.

Step #3: Factorization

    • We can factor out 3 from this expression to get:

12n2 + 36n + 35 = 3(4n2 + 12n + 11).

Step #4: Divisibility by 21

    • Since 4n2 + 12n + 11 is an integer, we have shown that the sum of the squares of any three consecutive odd integers is always a multiple of 21.

Question 6: Demonstrate that for the properties of the difference between the cubes of any two consecutive integers one obtains always an odd integer.

Solution:

Step #1: Assumptions and Setup

    • Let’s assume the two consecutive integers are n and n+1.
    • The difference between their cubes is (n+1)3 – n3.

Step #2: Expression Expansion

    • Expanding this expression, we get:

(n+1)3 – n3 = 3n2 + 3n + 1.

Step #3: Factorization

    • We can factor out 3 from this expression to get:

3n2 + 3n + 1 = 2(3n2 + 3n) + 1.

Step #4: Odd Integer

    • Since 3n2 + 3n is an even integer, we have shown that the difference between the cubes of any two consecutive integers is always an odd integer.

Question 7: Show that finding the sum of the squares of every two consecutive odd integers, the resultant will always be an even integer.

Solution:

Step #1: Assumptions and Setup

    • Let’s assume the two consecutive odd integers are 2n+1 and 2n+3.
    • The sum of their squares is (2n+1)2 + (2n+3)2.

Step #2: Expression Expansion

    • Expanding this expression, we get:

(2n+1)2 + (2n+3)2 = 8n2 + 24n + 20.

Step #3: Factorization

    • We can factor out 4 from this expression to get:

8n2 + 24n + 20 = 4(2n2 + 6n + 5).

Step #4: Even Integer

    • Since 2n2 + 6n + 5 is an odd integer, we have shown that the sum of the squares of any two consecutive odd integers is always an even integer.

Question 8: Illustrate that the item of any two consecutive odd integers is always odd.

Solution:

Step #1: Assumptions and Setup

    • Let the two consecutive odd integers be 2n + 1 and 2n + 3.
    • Their product is (2n + 1) × (2n + 3) = 4n2 + 10n + 3.

Step #2: Factoring Out 2

    • We can express this as 2(2n2 + 5n + 1) + 3.

Step #3: Odd Integer

    • Since 2n2 + 5n + 1 is an integer, and we have added an odd number (3), the product of any two consecutive odd integers is always odd.

Question 9: Show that the product of three consecutive even numbers are always divisible by 16.

Solution:

Step #1: Assumptions and Setup

    • Let the three consecutive even integers be 2n, 2n + 2, and 2n + 4.
    • Their product is 8n3 + 24n2 + 16n = 16(n3 + 3n2 + n).

Step #2: Divisibility by 8

    • Since the product contains at least three even numbers, it is divisible by 8.

Step #3: Divisibility by 16

    • Furthermore, it is divisible by 24 = 16 because n3 + 3n2 + n is always an integer.

Question 10: Show that the difference of the squares of any two consecutive odd integers is always a multiple of 8.

Solution:

Step #1: Assumptions and Setup

    • Let the two consecutive odd integers be 2n + 1 and 2n + 3.
    • Their squares are (2n + 1)2 = 4n2 + 4n + 1 and (2n + 3)2 = 4n2 + 12n + 9.

Step #2: Calculating the Difference

    • The difference between these two squares is

(2n + 3)2 – (2n + 1)2 = 8n + 8 = 8(n + 1).

Step #3: Multiples of 8

    • Therefore, the difference between the squares of any two consecutive odd integers is always a multiple of 8.