Algebraic Fractions | GCSE Maths

Practice Questions
Downloads

Introduction to Algebraic Fractions

What Are Algebraic Fractions?

  • An algebraic fraction is a fraction where the numerator, denominator, or both contain algebraic expressions (letters and numbers). For example:

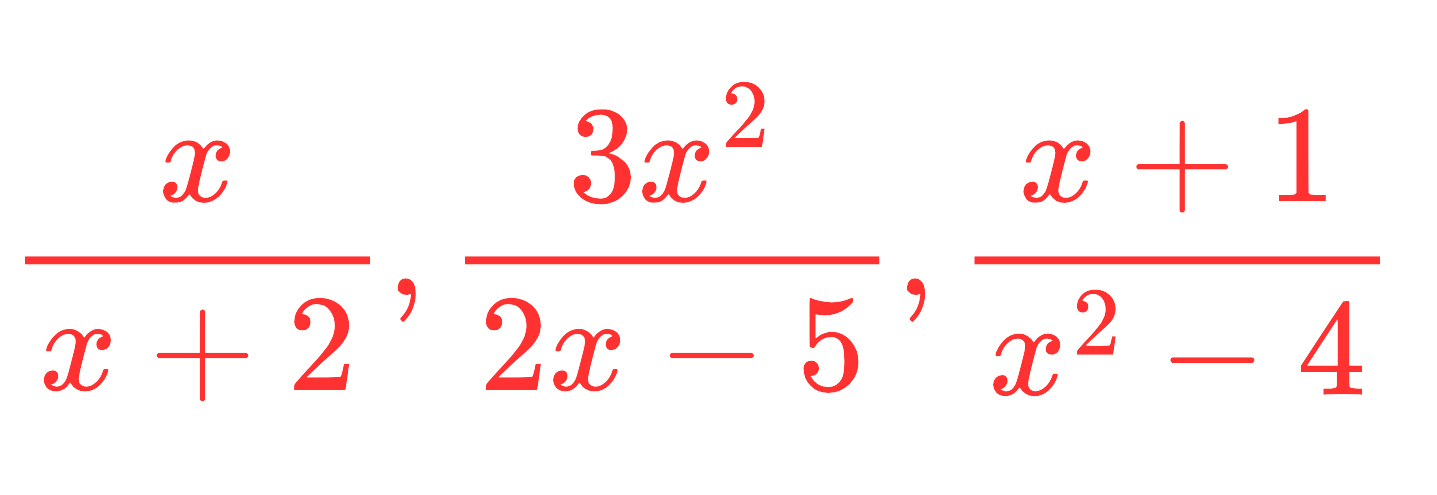
Examples of algebraic fractions where the numerator and denominator contain algebraic expressions with variables and numbers.

  • These work similarly to numerical fractions but follow algebraic rules when simplifying, adding, subtracting, multiplying, or dividing.

How Are Algebraic Fractions Different from Numerical Fractions?

Comparison table between numerical fractions and algebraic fractions, highlighting their components and examples.

What Skills Do You Need to Learn Algebraic Fractions?

  • Before working with algebraic fractions, you should be comfortable with the following topics:

1. Simplifying numerical fractions – Understanding how to reduce fractions by cancelling common factors.

2. Adding and subtracting fractions – Knowing how to find the lowest common denominator (LCD).

3. Factorisation – Being able to factorise expressions x2 – 4 into (x – 2).

4. Basic algebraic manipulation – Expanding brackets, simplifying expressions, and rearranging equations.

If you’re not confident with any of these, click the links below to review them before continuing:

Simplifying Algebraic Fractions

  • Simplifying algebraic fractions means reducing them to their simplest form by cancelling out common factors in the numerator and denominator, just like with numerical fractions.

Steps to Simplify Algebraic Fractions

1. Factorise the numerator and denominator – If possible, rewrite them as products of factors.

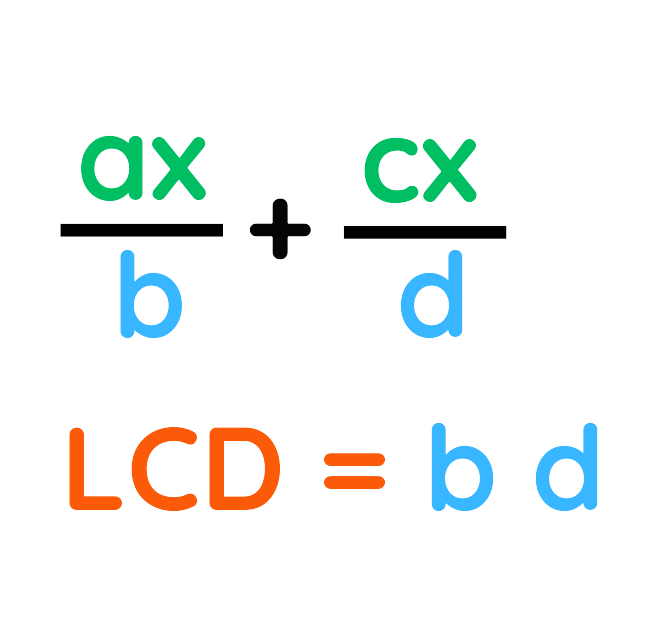
2. Cancel out common factors – Any factor that appears in both the numerator and denominator can be cancelled.

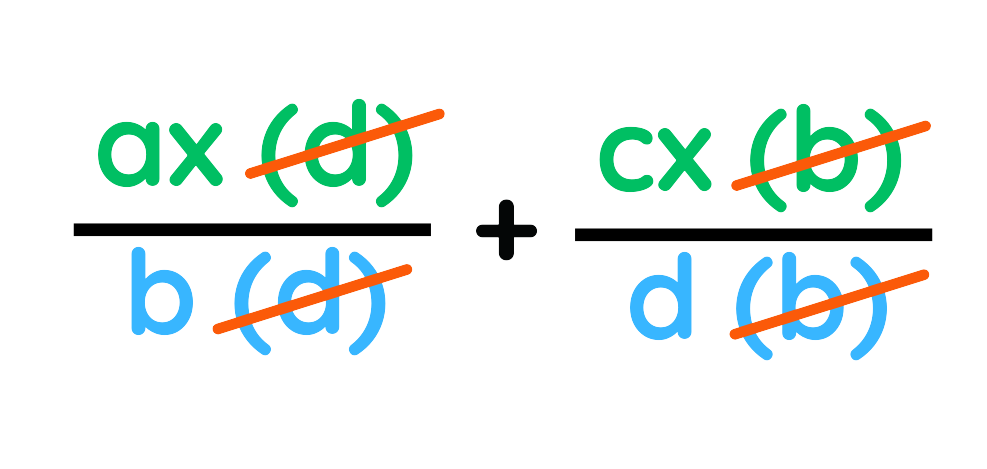
3. Write the simplified fraction – Once all common factors are removed, write the remaining expression.

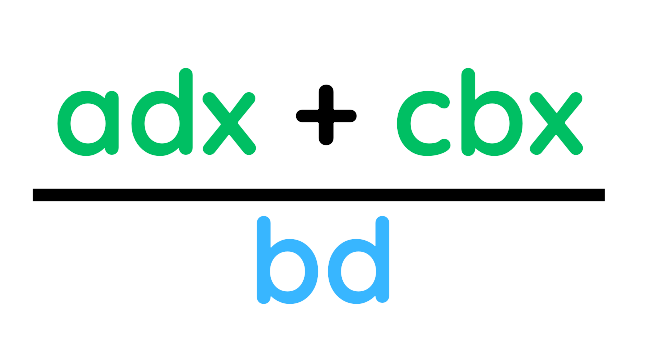
certified Physics and Maths tutorSolved Example: Simplifying a Basic Algebraic Fraction

Problem: Simplify: 

Algebraic fraction displaying (x^2 - 9) / (x + 3), illustrating factorization in algebraic expressions.

Solution: 

Step #1: Factorise the numerator:

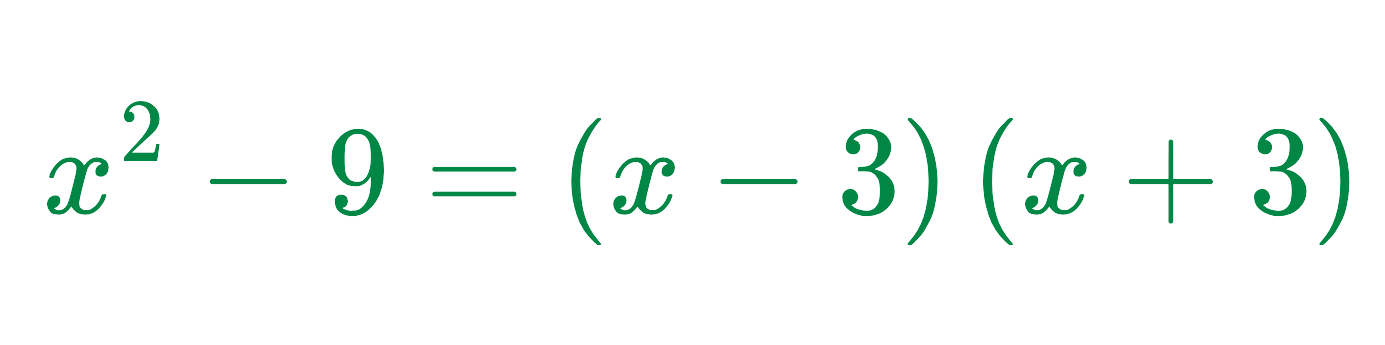
Algebraic expression showing the factorization of x^2 - 9 into (x - 3)(x + 3), demonstrating the difference of squares rule.

So, the fraction becomes:

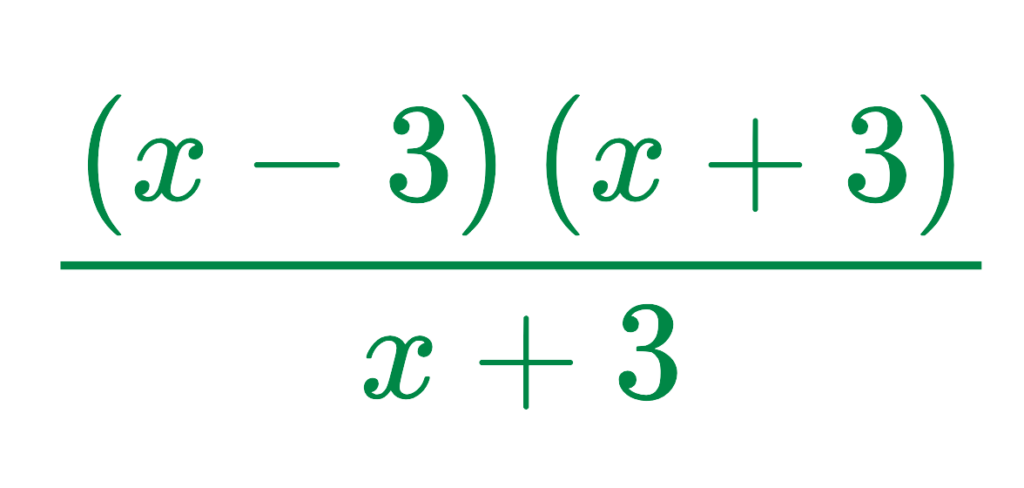
Algebraic fraction showing the simplification of (x - 3)(x + 3) / (x + 3) by canceling the common factor (x + 3).

Step #2: Cancel out common factors:

    • The (x + 3) cancels out, leaving:

x – 3

Final Answer: x – 3

certified Physics and Maths tutorSolved Example: Simplifying a More Complex Algebraic Fraction

Problem: Simplify: 

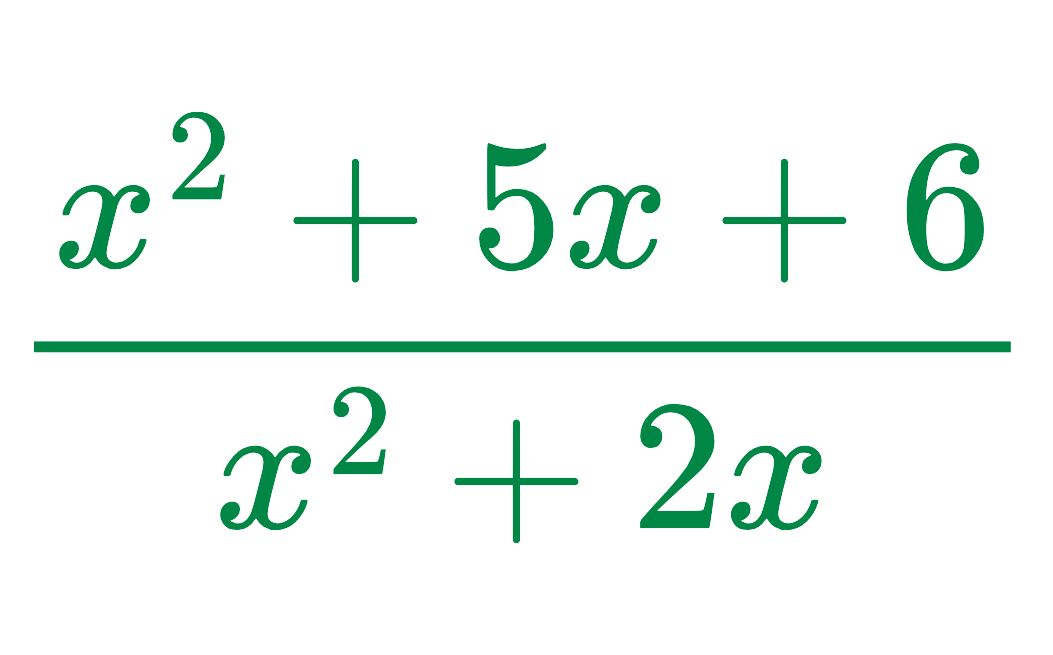
An algebraic fraction displaying (x^2 + 5x + 6) / (x^2 + 2x), demonstrating simplification through factoring and canceling common terms.

Solution: 

Step #1: Factorise the numerator and denominator:

Factorising the numerator:

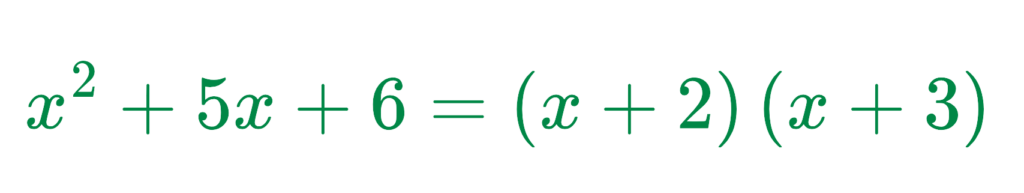
A quadratic expression x^2 + 5x + 6 factored into (x + 2)(x + 3), demonstrating algebraic factorization.

Factorising the denominator:

A quadratic expression x^2 + 2x factored into x(x + 2), illustrating the process of factoring out the greatest common factor.

Now, the fraction becomes:

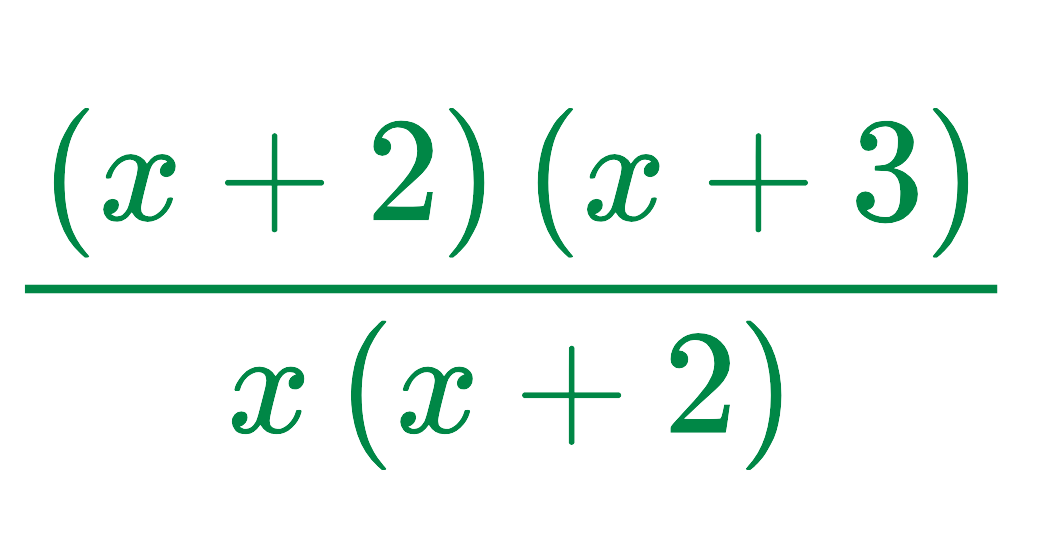
An algebraic fraction showing (x + 2)(x + 3) / x(x + 2), illustrating the simplification process by canceling common factors.

Step #2: Cancel out common factors:

    • The (x + 2) cancels out, leaving:

simplified algebraic fraction (x + 3) / x representing a rational expression in its simplest form.

Final Answer: x + 3/ x

Adding and Subtracting Algebraic Fractions

  • When adding or subtracting algebraic fractions, the process is similar to numerical fractions—you need a common denominator before combining the fractions.

Steps to Add or Subtract Algebraic Fractions

1. Find the Lowest Common Denominator (LCD) – Identify the smallest common multiple of the denominators.

2. Adjust the numerators – Rewrite each fraction so they have the same denominator.

3. Add or subtract the numerators – Keep the denominator the same and simplify the numerator if possible.

4. Simplify the fraction – Factorise if needed and cancel common factors.

certified Physics and Maths tutorSolved Example: Adding Algebraic Fractions with the Same Denominator

Problem: Simplify: 

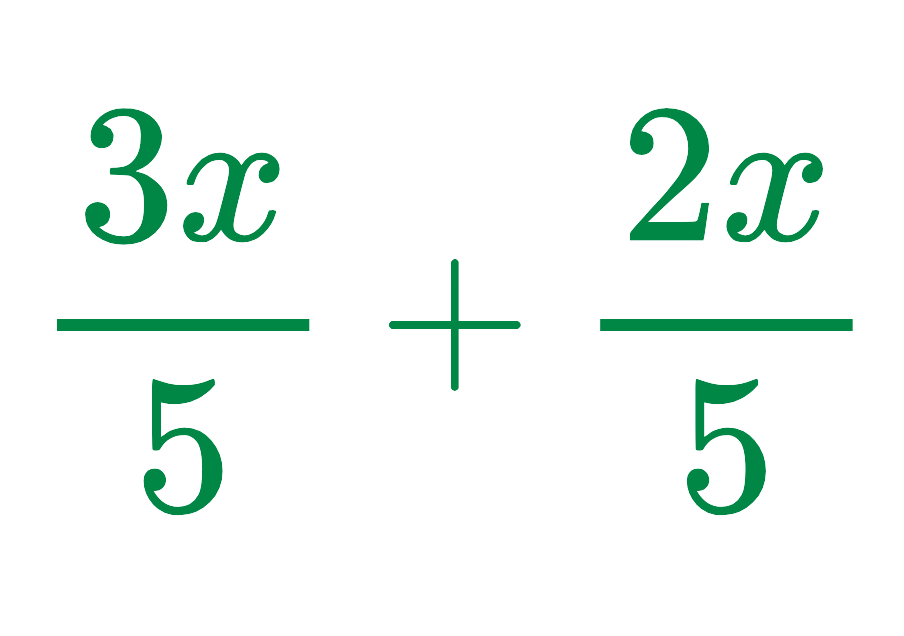
An algebraic fraction addition problem showing (3x / 5) + (2x / 5), demonstrating the addition of fractions with like denominators.

Solution: 

Since the denominator is already the same (5), simply add the numerators:

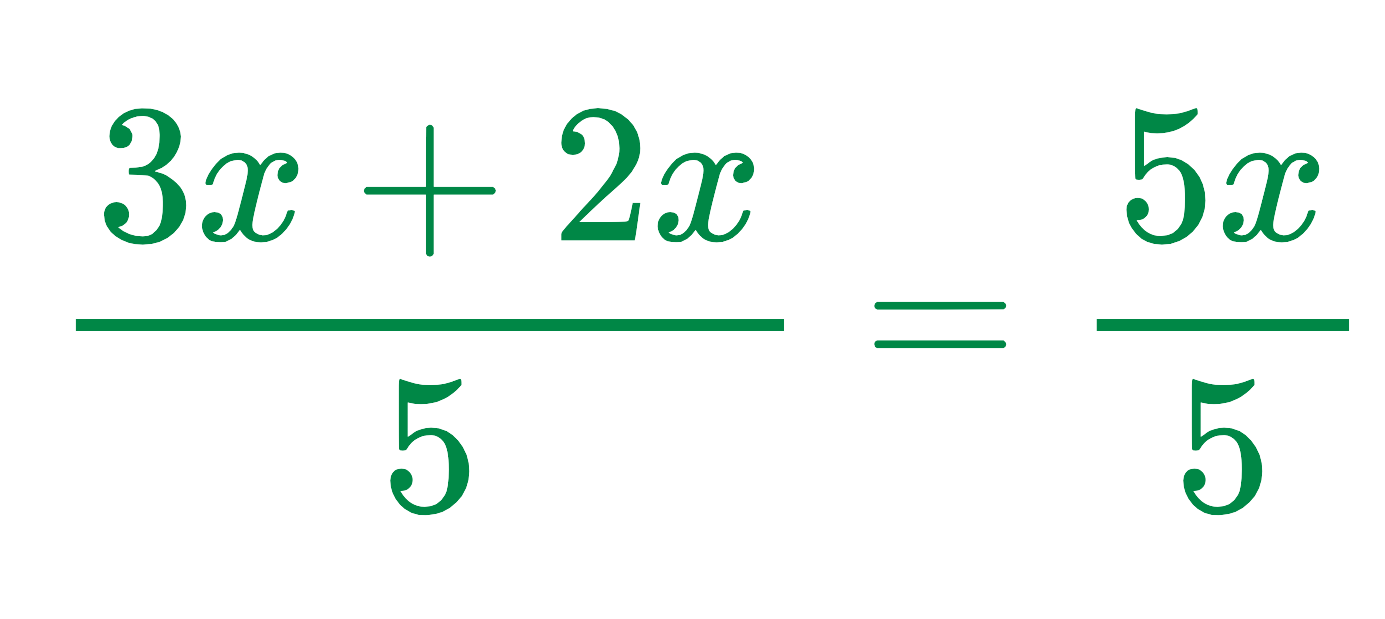
A mathematical simplification of algebraic fractions showing (3x + 2x) / 5 = 5x / 5, illustrating the addition of fractions with like denominators.

Final Answer: x

certified Physics and Maths tutorSolved Example: Adding Algebraic Fractions with Different Denominators

Problem: Simplify: 

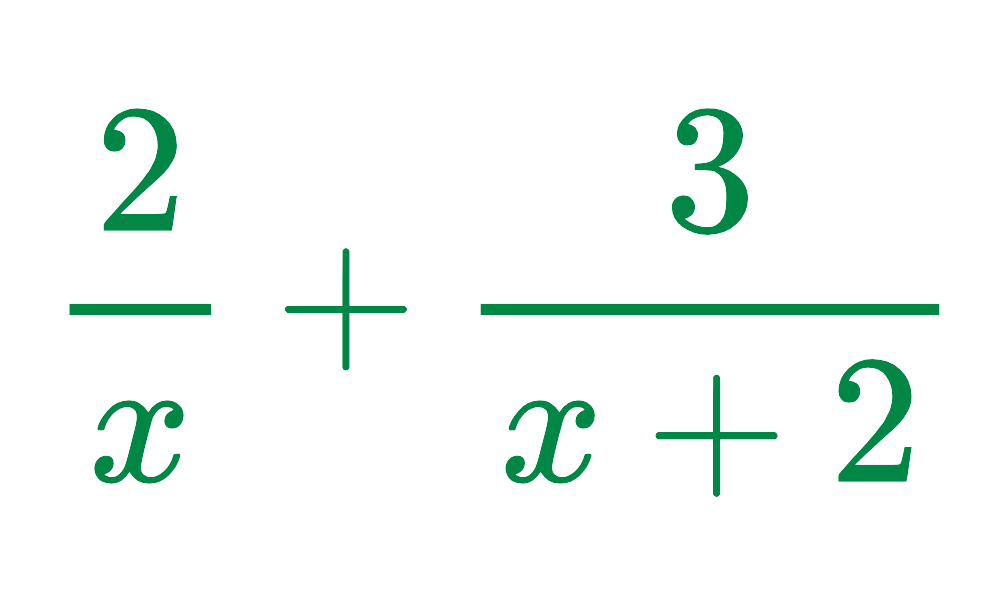
An algebraic fraction addition problem showing 2/x + 3/(x + 2), demonstrating the process of adding fractions with different denominators.

Solution: 

Step #1: Find the Lowest Common Denominator (LCD):

    • The denominators are x and x + 2, so the LCD is x(x + 2).

Step #2: Adjust the numerators:

    • Multiply each fraction so they both have the LCD:

Algebraic fraction addition showing 2(x + 2) / x(x + 2) + 3x / x(x + 2), demonstrating the use of a common denominator to simplify.

Expanding the numerators:

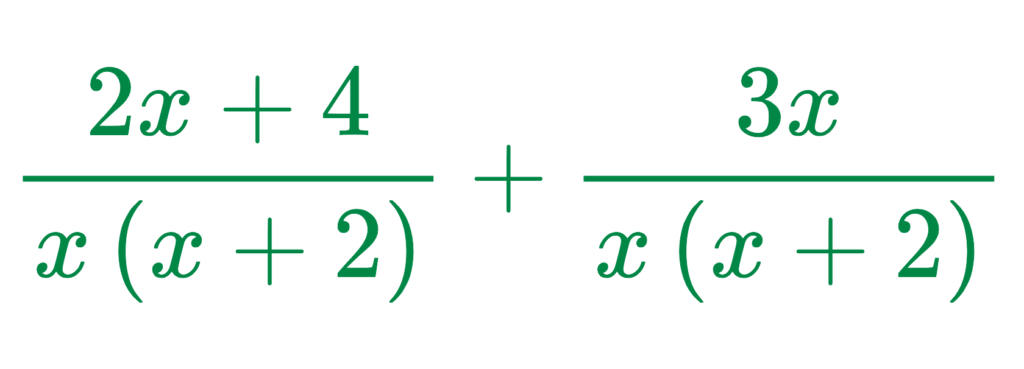
Algebraic fraction addition involving different numerators, shown as (2x + 4) / x(x + 2) + 3x / x(x + 2), demonstrating how to combine fractions with a common denominator.

Step #3: Add the numerators:

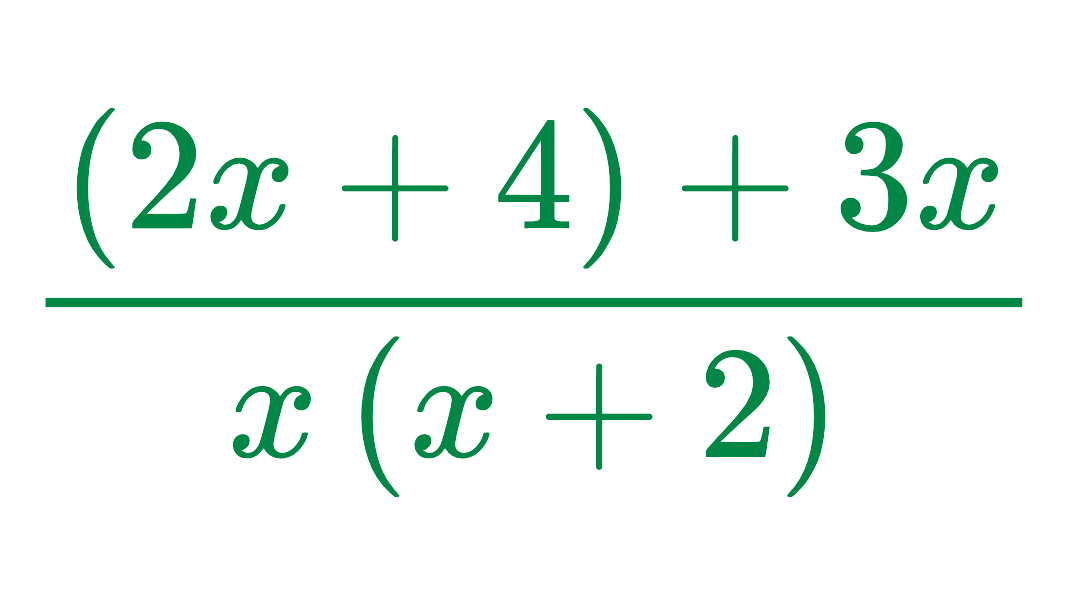
Algebraic fraction simplification step showing (2x + 4) + 3x over x(x + 2), demonstrating the combination of numerators over a common denominator.

Simplified algebraic fraction showing (5x + 4) over x(x + 2), representing the result of combining terms in a rational expression.

Final Answer: 5x + 4 / x(x + 2)

certified Physics and Maths tutorSolved Example: Subtracting Algebraic Fractions

Problem: Simplify: 

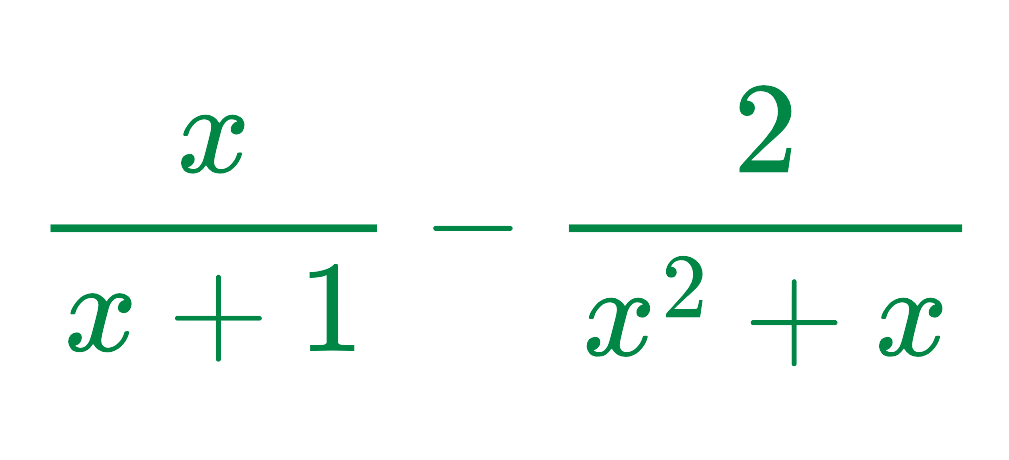
Algebraic fraction subtraction showing x/(x + 1) - 2/(x^2 + x), demonstrating the process of finding a common denominator.

Solution: 

  • To find the lowest common denominator (LCD), we first check if the denominators can be factorised. Here, x2 + x can be rewritten as x(x + 1).
  • Rewriting the fractions:

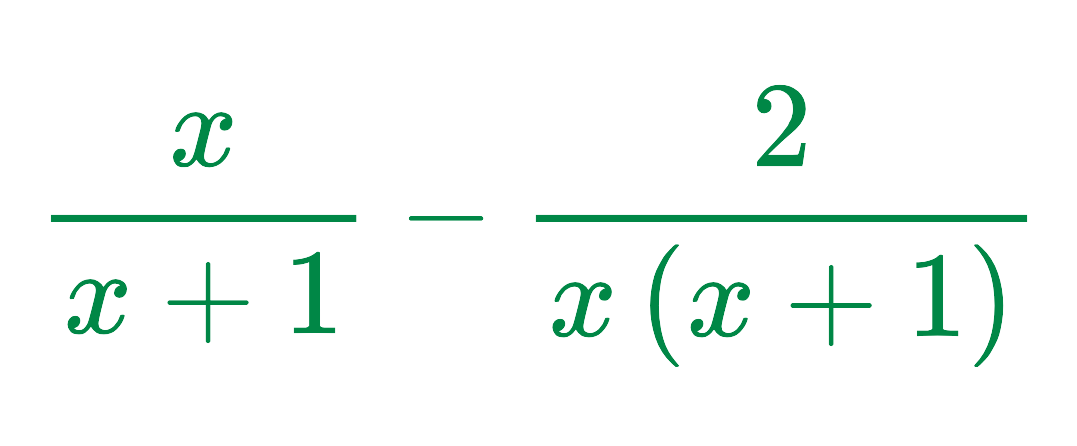
Subtracting algebraic fractions x/(x + 1) - 2/(x(x + 1)), demonstrating the process of finding a common denominator.

Step #1: Find the Lowest Common Denominator (LCD):

    • The denominators are x + 1 and x (x + 1). Since x (x + 1) already includes x + 1, the LCD is x (x + 1).
    • Now, adjust the first fraction to have this denominator by multiplying the numerator and denominator by x:

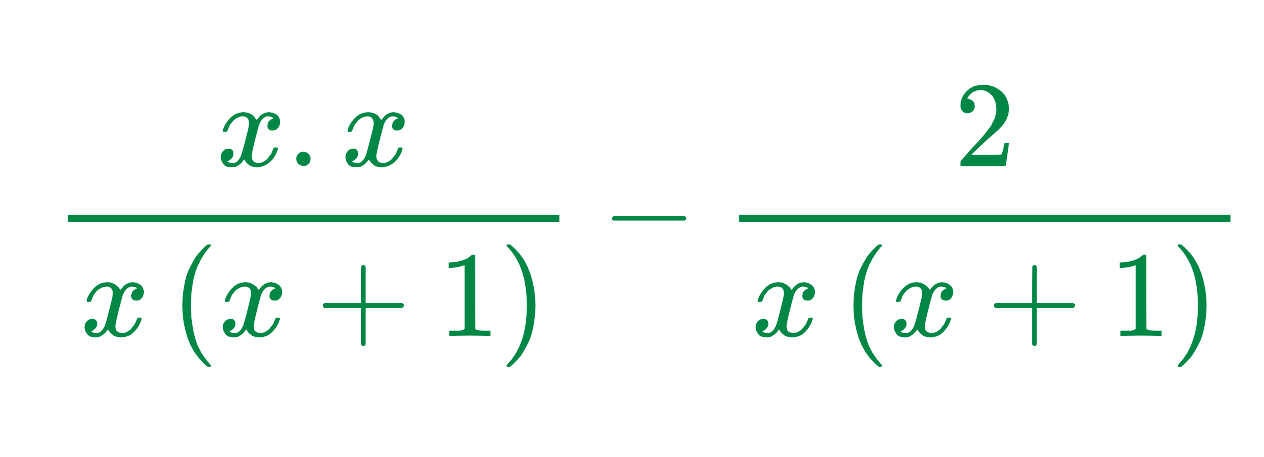
Subtracting algebraic fractions (x * x) / (x(x + 1)) - 2 / (x(x + 1)), demonstrating the simplification process.

This simplifies to:

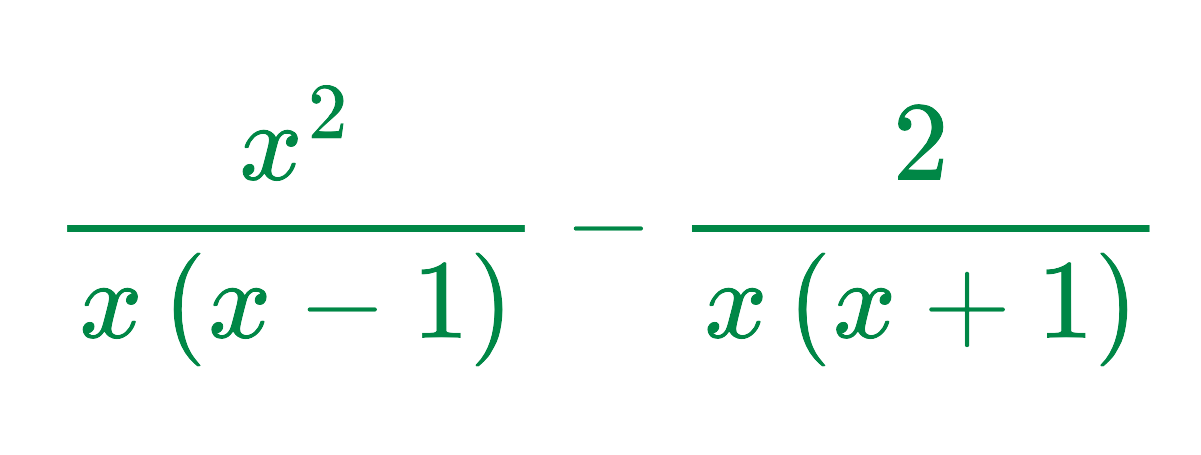
Subtracting algebraic fractions x^2 / (x(x - 1)) - 2 / (x(x + 1)), illustrating different denominators in rational expressions.

Step #2: Subtract the numerators:

    • Since the denominators are now the same, we subtract the numerators:

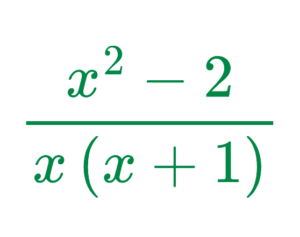
Algebraic fraction with polynomial numerator and factored denominator, represented as (x^2 - 2) / x(x + 1).

Final Answer: x2 – 2 / x(x + 1)

Multiplying and Dividing Algebraic Fractions

  • Multiplying and dividing algebraic fractions is more straightforward than addition and subtraction because you don’t need a common denominator. However, you should always factorise first and cancel common factors to simplify the expressions.

Multiplying Algebraic Fractions

To multiply algebraic fractions, follow these steps:

1. Factorise the numerators and denominators (if possible).

2. Cancel out any common factors in the numerator and denominator.

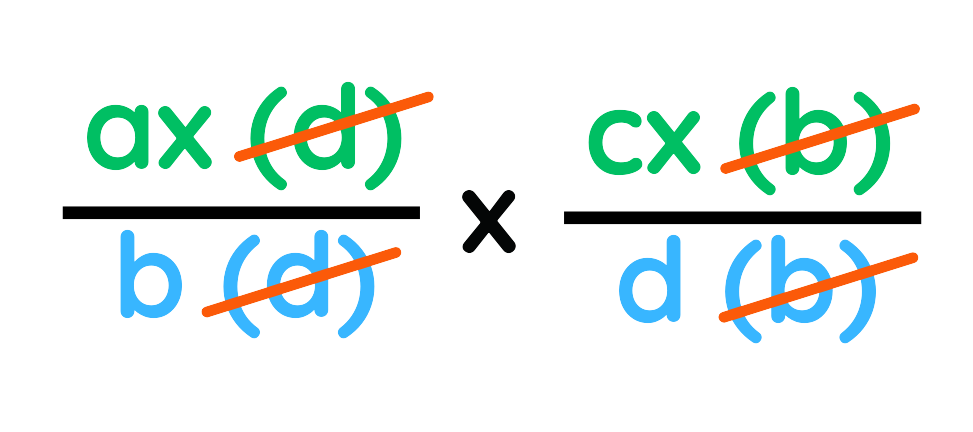
3. Multiply the numerators together and the denominators together.

4. Simplify the final expression if needed.

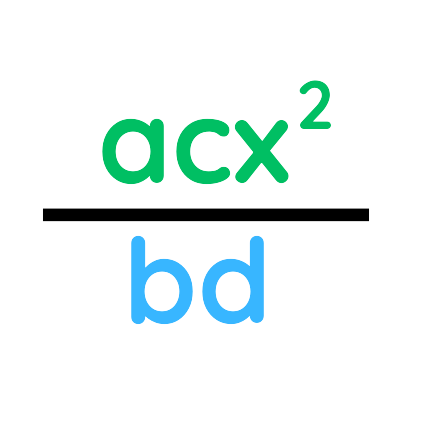
certified Physics and Maths tutorSolved Example: Multiplying Simple Algebraic Fractions

Problem: Simplify: 

Multiplication of two algebraic fractions, represented as (2x / 3) × (5 / 4x).

Solution: 

Step #1: Cancel common factors:

The x in the numerator and denominator cancels out:

Multiplication of two numerical fractions, represented as (2 / 3) × (5 / 4).

Step #2: Multiply the remaining terms:

Multiplication of fractions (2 × 5) / (3 × 4) showing the result as 10 / 12.

Step #3: Simplify the fraction:

Simplification of the fraction 10/12 to its lowest terms, 5/6.

Final Answer: 5/6

certified Physics and Maths tutorSolved Example: Multiplying More Complex Algebraic Fractions

Problem: Simplify: 

Multiplication of two algebraic fractions involving polynomials.

Solution: 

Step #1: Factorise the numerators and denominators:

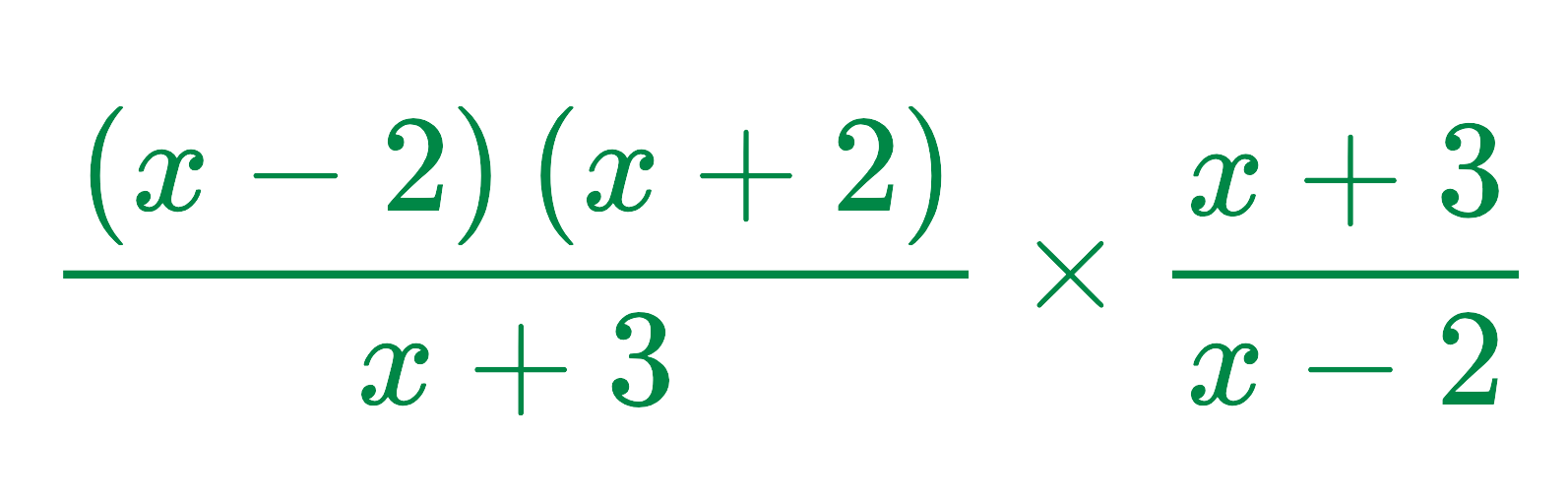
Multiplication of two algebraic fractions with factored polynomials.

Step #2: Cancel out common factors:

Cancel x + 3 and x − 2 from both fractions:

An algebraic fraction simplifying to a linear expression.

Final Answer: x + 2

If you’d like to explore Multiplying Algebraic Fractions in more depth, check out our detailed guide here:

Multiplying Algebraic Fractions – Full Explanation & Examples

Dividing Algebraic Fractions

To divide algebraic fractions, follow these steps:

1. Flip the second fraction (reciprocal) – Change division into multiplication.

For example:

Simply swap the numerator and denominator of the second fraction, then proceed as a multiplication problem.

2. Factorise the numerators and denominators if possible.

3. Cancel out common factors in the numerator and denominator.

4. Multiply the remaining terms and simplify.

certified Physics and Maths tutorSolved Example: Dividing Algebraic Fractions

Problem: Simplify: 

Solution: 

Step #1: Flip the second fraction and change to multiplication:

Step #2: Factorise the numerator and denominator:

Since x2 − 9 is a difference of squares:

Step #3: Cancel out common factors:

The x + 3 cancels out:

Step #4: Multiply the remaining terms:

Final Answer: (x – 3)(x + 2) / x + 4

Solving Equations Involving Algebraic Fractions

  • Equations with algebraic fractions often require removing the fractions before solving for the variable. The key is to find the Lowest Common Denominator (LCD) and use it to eliminate fractions.

Steps to Solve Equations with Algebraic Fractions

  1. Find the Lowest Common Denominator (LCD) – Identify the smallest multiple of all denominators.
  2. Multiply the entire equation by the LCD – This eliminates fractions.
  3. Solve the resulting equation – Expand, simplify, and solve for the variable.
  4. Check for restrictions – Ensure the final answer does not make any denominator zero (as division by zero is undefined).

certified Physics and Maths tutorSolved Example: Solving a Simple Algebraic Fraction Equation

Problem: Solve for x: 

Solution: 

Step #1: Find the Lowest Common Denominator (LCD):

The denominators are 3 and 5, so the LCD is 15

Step #2: Multiply the entire equation by 15:

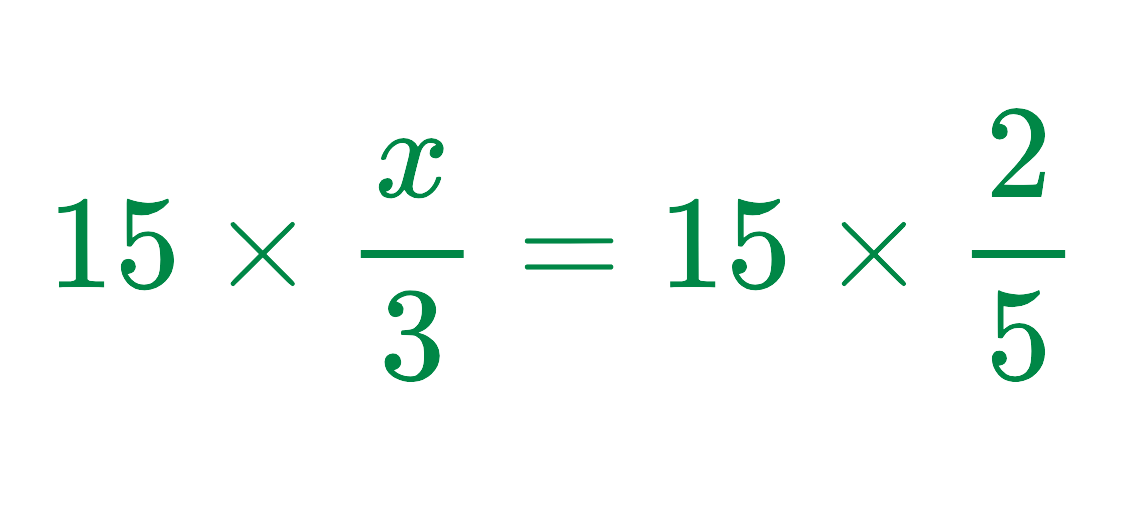
Step #3: Simplify:

Step #4: Solve for x:

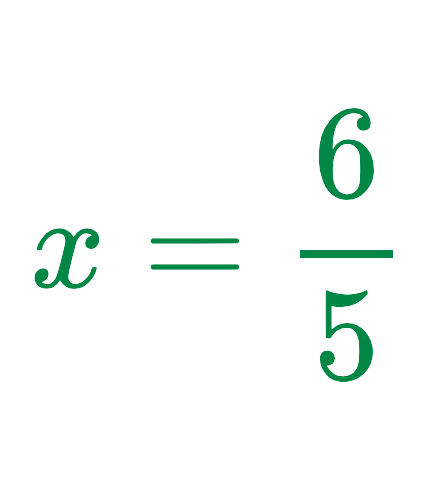
Final Answer: x = 6/5

certified Physics and Maths tutorSolved Example: Solving an Equation with Multiple Algebraic Fractions

Problem: Solve for x: 

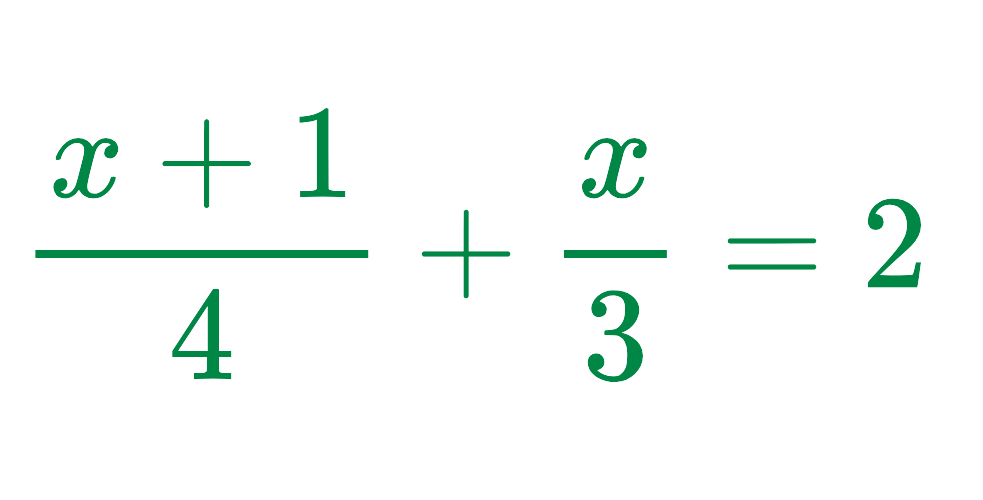
Solution: 

Step #1: Find the Lowest Common Denominator (LCD):

The denominators are 4 and 3, so the LCD is 12

Step #2: Multiply the entire equation by 12:

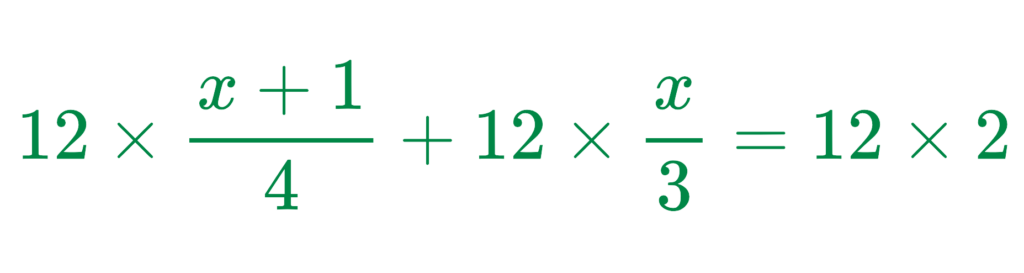
Step #3: Simplify:

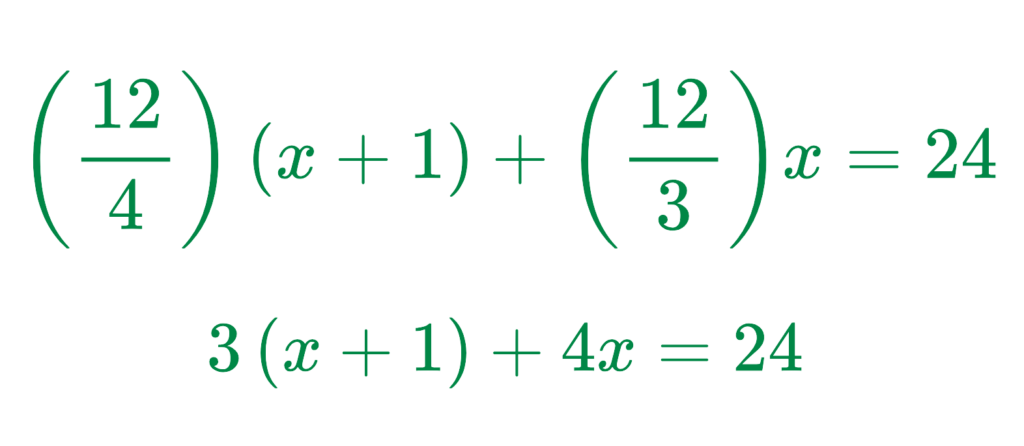
Step #4: Expand and Solve:

Final Answer: x = 3

certified Physics and Maths tutorSolved Example: Solving an Equation with a Variable in the Denominator

Problem: Solve for x: 

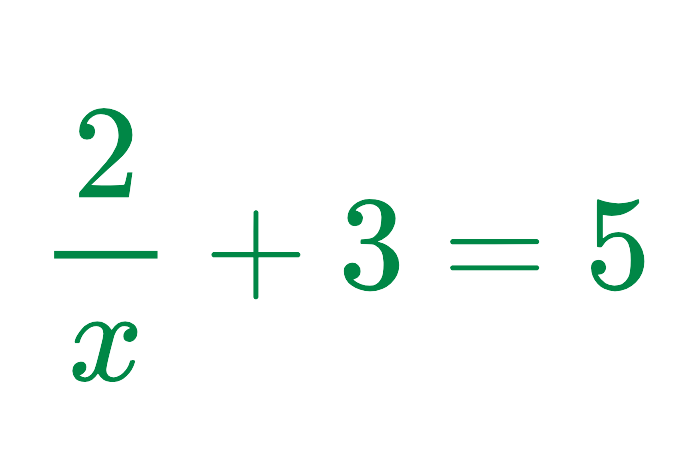
Solution: 

Step #1: Isolate the fraction:

Subtract 3 from both sides:

Step #2: Multiply by x to remove the fraction:

Step #3: Solve for x:

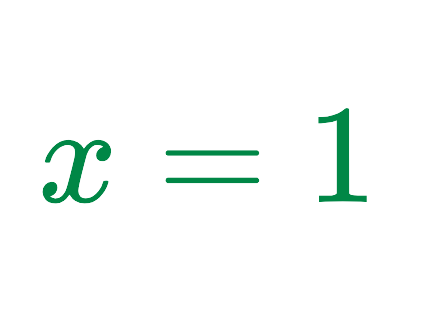
Final Answer: x = 1

How to Solve Equations with Algebraic Fractions – GCSE Higher Maths

  • In order to solve equations with algebraic fractions, the key is to find the Lowest Common Denominator (LCD) to eliminate fractions.

Steps to Solve Equations with Algebraic Fractions

  1. Find the Lowest Common Denominator (LCD) – Identify the smallest multiple of all denominators.
  2. Multiply the entire equation by the LCD – This removes fractions from the equation.
  3. Solve the resulting equation – Expand, simplify, and solve for the variable.

certified Physics and Maths tutor Edexcel GCSE Maths – November 2022 Paper 1 – Algebraic Fractions Question

Problem: Solve: 

Give your answer in the form a ± b√2 , where a and b are fractions.

Solution: 

Step #1: Find the Lowest Common Denominator (LCD):

The denominators are x and x + 1, so the LCD is:

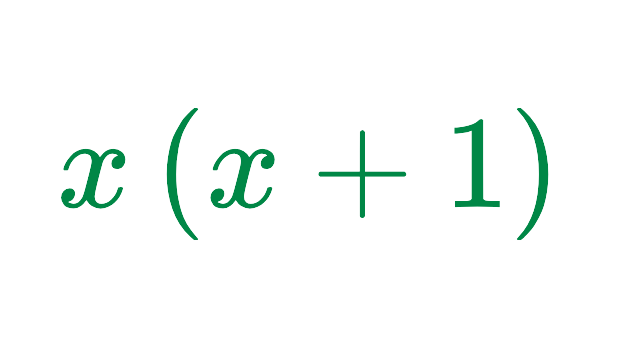
Multiply each fraction to express them with the LCD:

Now, simplify the numerators:

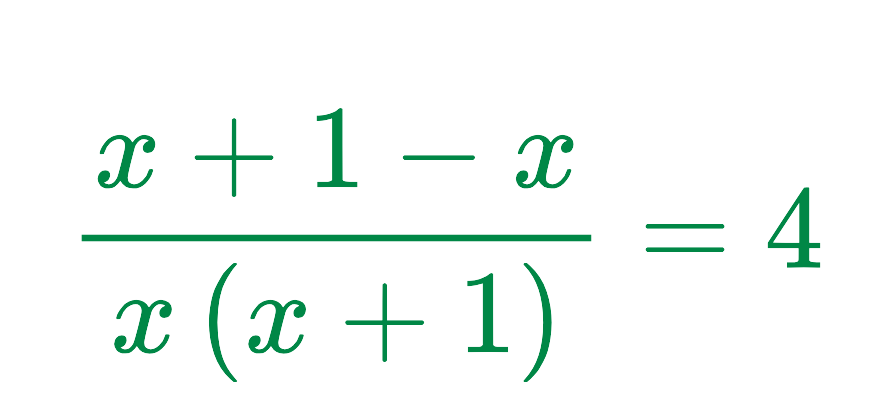
Step #2: Multiply Both Sides by the Denominator:

The denominators are x and x + 1, so the LCD is:

1 = 4x(x + 1)

Expand the right-hand side:

1 = 4x2 + 4x

Rearrange to form a quadratic equation:

4x2 + 4x – 1 = 0

Step #3: Solve the Quadratic Equation Using the Quadratic Formula:

4x2 + 4x – 1 = 0

Using the quadratic formula:

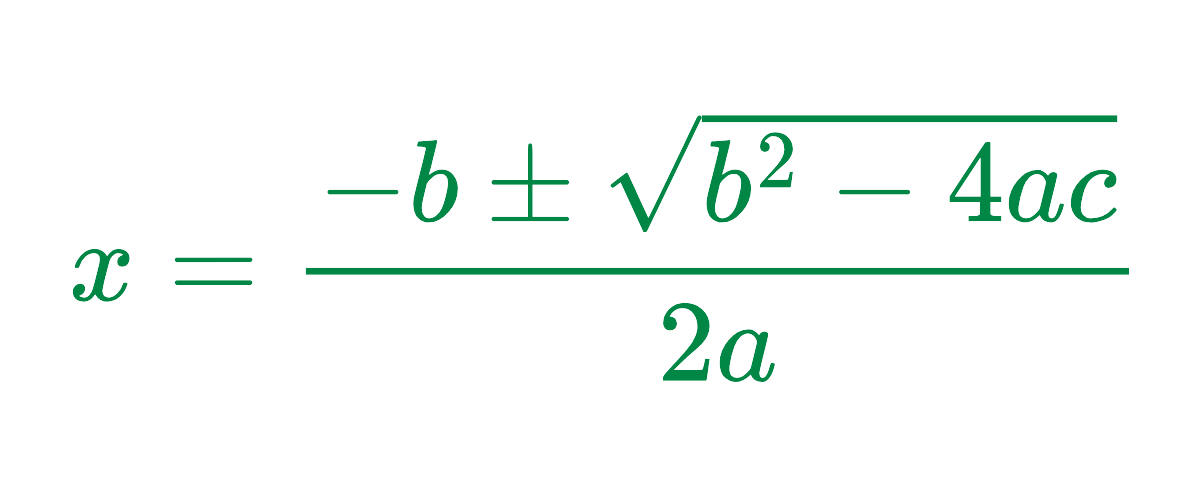
where:

    • a = 4,
    • b = 4,
    • c = -1

First, calculate the discriminant:

b² – 4ac = (4)² – 4(4)(-1)

= 16 + 16 = 32

Since 32 = 16 × 2, we can simplify:

√32 = 4√2

Now, substitute into the quadratic formula:

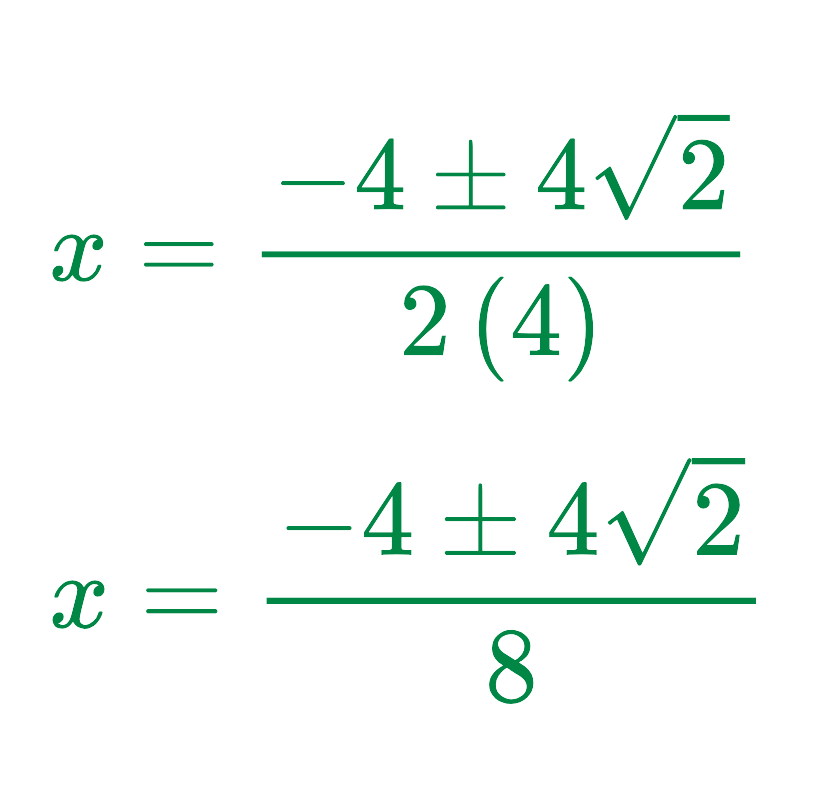
Step #4: Express in the Required Form:

Simplify the fraction:

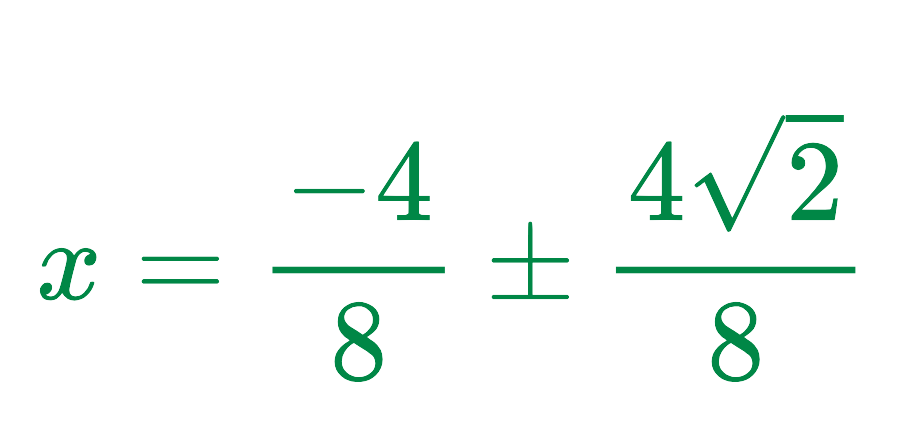
Final Answer: x = – 1/2 ± (√2 / 2)

This matches the required form a ± b√2, where:

      • a = -1/2
      • b = 1/2

Conclusion

  • Algebraic fractions are an essential part of GCSE Higher Maths, appearing in various topics like simplifying expressions, solving equations, and performing operations such as addition, subtraction, multiplication, and division.
  • Mastering these skills will not only help in exams but also build a strong foundation for advanced algebra.
  • To strengthen your understanding, practice with the resources below:

Algebraic Fractions Worksheet

Simplifying Algebraic Fractions Worksheet

Algebraic Fractions GCSE Questions

Algebraic Fractions Solutions

If you’d like to explore Multiplying Algebraic Fractions in more depth, check out our detailed guide here:

Practice Questions and Answers on Algebraic Fractions

Question 1: Simplify:

(x² – 4) / (x + 2)

Question 2: Simplify:

(x² + 6x + 9) / (x² + 3x)

Question 3: Simplify:

(x² – x – 6) / (x² – 4x + 4)

Question 4: Simplify:

(x² – 9) / (x² – 6x + 9)

Question 5: Simplify:

(x³ – x) / (x² – x)

Question 6: Simplify:

(2x² + 4x) / (x² + 2x + 1)

Question 7: Simplify:

(x² – 5x + 6) / (x² – 2x – 3)

Question 8: Simplify:

(x³ – 8) / (x² – 4x + 4)

Question 9: Simplify:

(x² – 7x + 10) / (x² – x – 20)

Question 10: Simplify:

(x³ – x + 1) / (x² – 1)

Solutions

Question 1: 

Solution:

Factorise the numerator:

x² – 4 = (x – 2)(x + 2)

Cancel the common factor (x + 2):

(x – 2)(x + 2) / (x + 2) = x – 2

Final Answer: x – 2

 

Question 2:

Solution:

Factorise the numerator and denominator:

x² + 6x + 9 = (x + 3)(x + 3)

x² + 3x = x(x + 3)

Cancel the common factor (x + 3):

(x + 3)(x + 3) / (x(x + 3)) = (x + 3) / x

Final Answer: (x + 3) / x

 

Question 3:

Solution:

Factorise both numerator and denominator:

x² – x – 6 = (x – 3)(x + 2)

x² – 4x + 4 = (x – 2)(x – 2)

No common factors cancel.

Final Answer: (x – 3)(x + 2) / (x – 2)(x – 2)

 

Question 4:

Solution:

Factorise numerator and denominator:

x² – 9 = (x – 3)(x + 3)

x² – 6x + 9 = (x – 3)(x – 3)

Cancel x – 3:

(x – 3)(x + 3) / (x – 3)(x – 3) =

(x + 3) / (x – 3)

Final Answer: (x + 3) / (x – 3)

 

Question 5: 

Solution:

Factorise:

x(x² – 1) / x(x – 1)

Factorise x² – 1:

x(x – 1)(x + 1) / x(x – 1)

Cancel x – 1:

(x + 1)

Final Answer: x + 1

 

Question 6: 

Solution:

Factorise the numerator and denominator:

2x² + 4x = 2x(x + 2)

x² + 2x + 1 = (x + 1)(x + 1)

No common factors cancel.

Final Answer: (2x(x + 2)) / ((x + 1)(x + 1))

 

Question 7: 

Solution:

Factorise:

(x – 2)(x – 3) / (x – 3)(x + 1)

Cancel x – 3:

(x – 2) / (x + 1)

Final Answer: (x – 2) / (x + 1)

 

Question 8: 

Solution:

Factorise numerator and denominator:

(x – 2)(x² + 2x + 4) / (x – 2)(x – 2)

Cancel x – 2:

(x² + 2x + 4) / (x – 2)

Final Answer: (x² + 2x + 4) / (x – 2)

 

Question 9: 

Solution:

Factorise the numerator and denominator:

x² – 7x + 10 = (x – 5)(x – 2)

x² – x – 20 = (x – 5)(x + 4)

Cancel x – 5:

(x – 5)(x – 2) / (x – 5)(x + 4) = (x – 2) / (x + 4)

Final Answer: (x – 2) / (x + 4)

 

Question 10: 

Solution:

Factorise the denominator:

x² – 1 = (x – 1)(x + 1)

No common factors cancel.

Final Answer: (x³ – x + 1) / ((x – 1)(x + 1))

Table of Content

Join Tutoring