A-Level : Straight Line Equation | Practice Questions with Examples

In this tutorial, we will explore one of the most fundamental concepts in algebra: the four basic forms that are important for A-Level : straight-line equation.

Practice Questions
Downloads

Video Tutorial on A-Level : Straight Line Equation

  • Watch this Video Tutorial as we explain all types of Straight Line Equations for A-Level Maths

The Four Basic Forms of a Straight-Line Equation

The Four Basic forms of a Straight-Line Equation are essential for solving linear equations and understanding the geometry of straight lines in A-level mathematics.

  • The Four Forms We will discuss are:
  1. Slope-Intercept Form
  2. Point-Slope Form
  3. Two-Point Form
  4. Standard Form

They are very important in practicing questions for coordinate geometry as well.

Here is one more link to practice a few extra questions: Maths Genie Straight Line Equation Questions

Slope-Intercept Form

The Slope-Intercept form is the most commonly used equation of a straight line.

It expresses the line in terms of its slope and y-intercept, making it easy to graph and analyze.

Formula

The slope-intercept form is written as:

  • y = m x + c

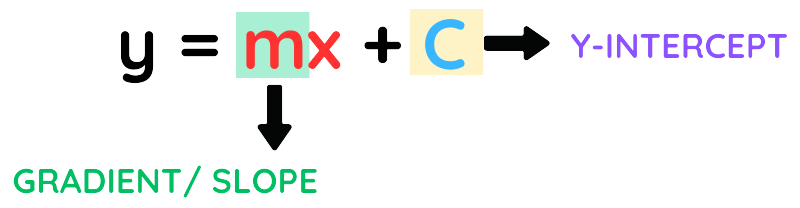
A-Level: Straight Line Equation showing the slope-intercept form y = mx + c where m is the gradient and c is the y-intercept.

Where:

    • m is the slope or gradient of the line.
    • C is the y-intercept, the point where the line crosses the y-axis.

Understanding the Slope (Gradient)

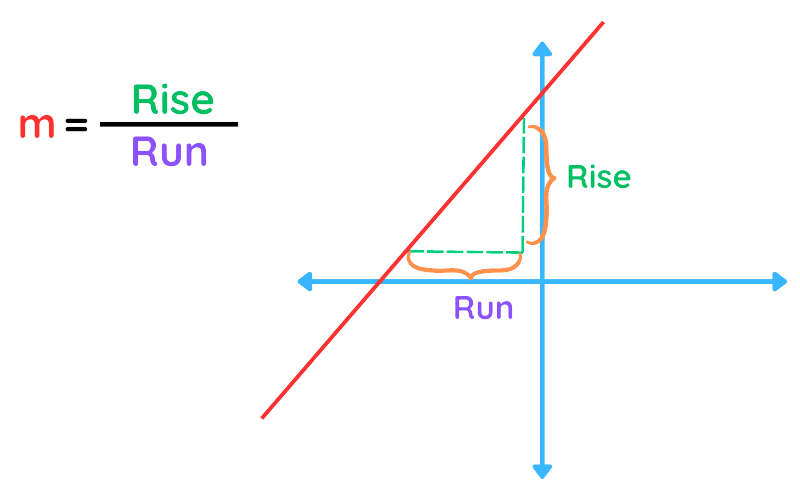
The slope indicates how steep the line is.

It is calculated as the ratio of the vertical change (rise) to the horizontal change (run) between two points on the line.

  • Slope (m) = Rise / Run

A-Level: Straight Line Equation showing the slope formula m = Rise/Run.

  • Alternatively, m = Change in y / Change in x

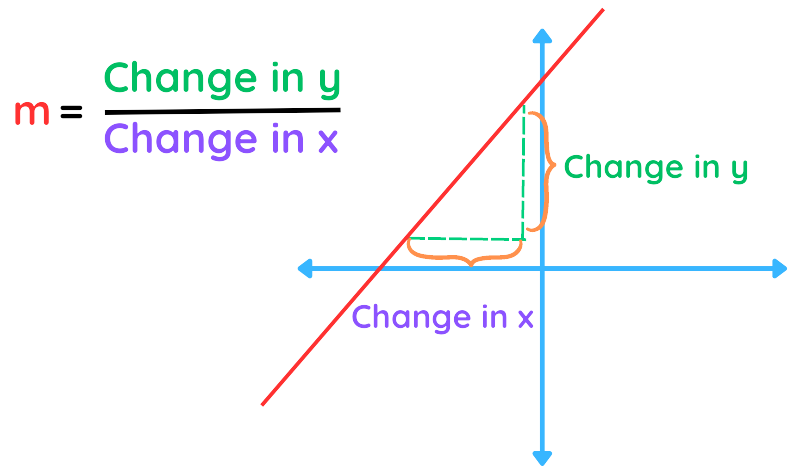
A-Level: Straight Line Equation illustrating the slope as the ratio of change in y to change in x.

A positive slope means the line rises as it moves from left to right, while a negative slope means it falls.

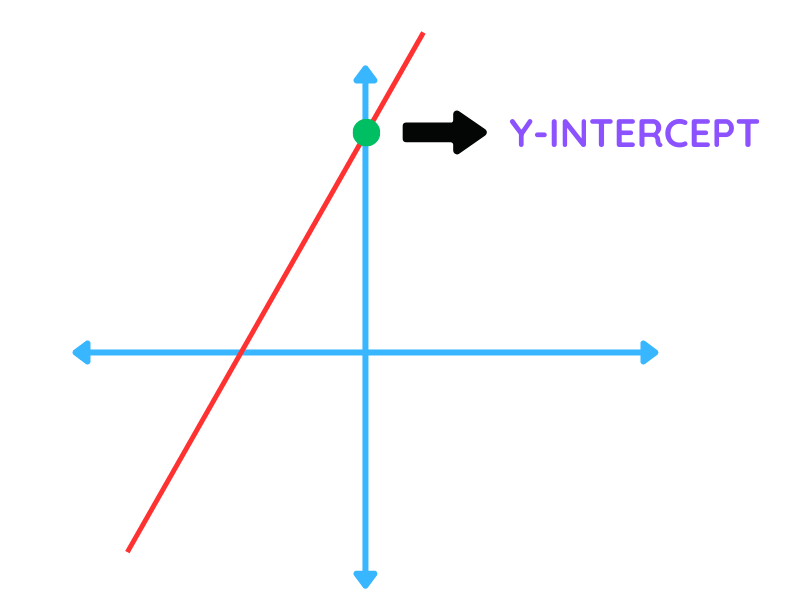
Understanding the Y-Intercept

The y-intercept (c) is the value of y where the line crosses the y-axis (when x = 0).

It indicates the starting point of the line on the y-axis.

A-Level: Straight Line Equation showing the y-intercept where the line crosses the y-axis.

certified Physics and Maths tutor

 

 

Solved Example 1

Question: Given the equation of the line y = -3 x + 5, find the gradient and the Y-intercept

Solution: 

  • Slope (m): -3
  • Y-intercept (c): 5

Interpretation:

  • The line crosses the y-axis at the point (0, 5).
  • The negative slope of -3 indicates that for every unit increase in x,  y decreases by 3 units. The line slopes downward from left to right.

Steps to Draw the Graph:

  • Starting at the y-intercept plot the point (0, 5)
  • Move down 3 units and right 1 unit to plot the next point.
  • Connect the points to draw the line.

A-Level: Straight Line Equation with a slope of -3 and a y-intercept of 5.

certified Physics and Maths tutor

 

 

Solved Example 2: Finding the Equation from a Graph

Question: What is the Equation of the Straight Line shown below

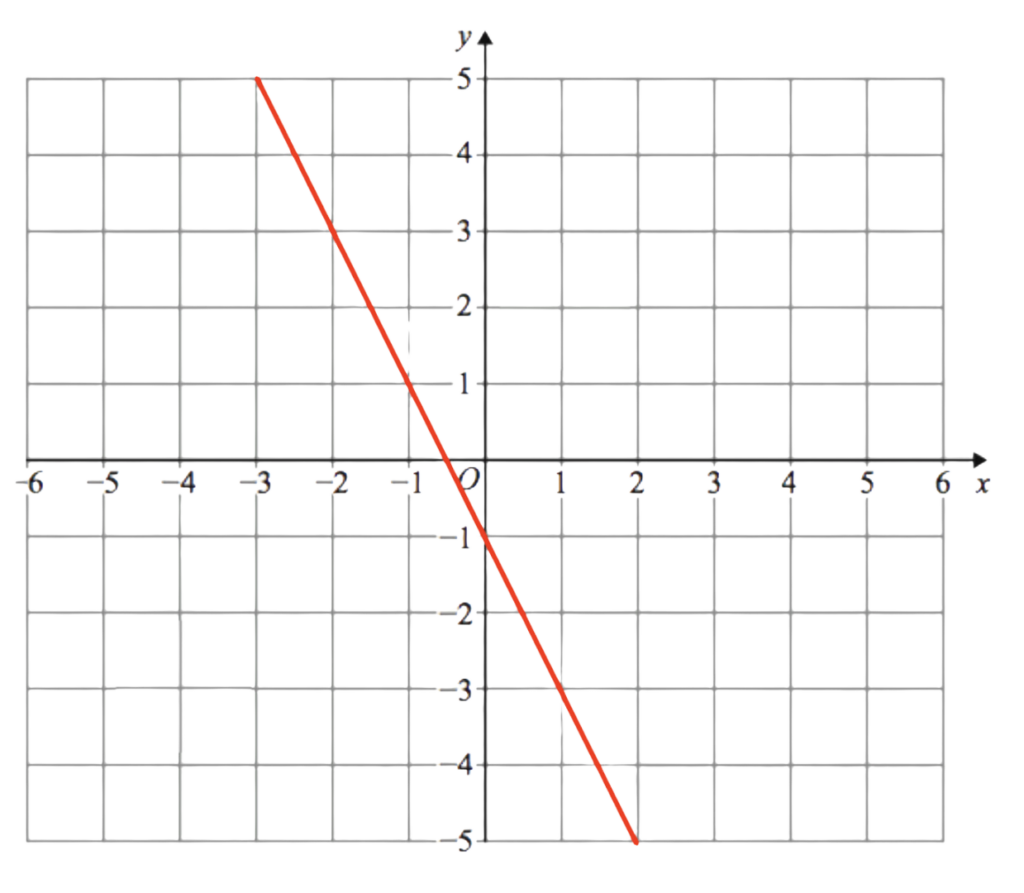
Graph displaying a straight line equation in a Cartesian plane for A-Level mathematics.

Solution: 

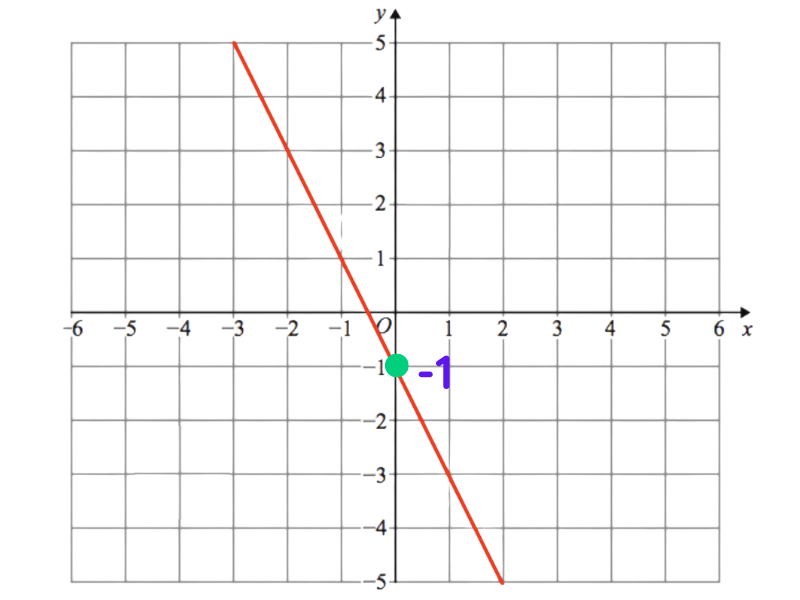
Step 1: Find the Y-Intercept (c) 

  • Look at where the line crosses the y-axis.
  • For example, if the line crosses the y-axis at y = -1, then c = -1.

A straight line graph showing the slope and y-intercept at y=−1

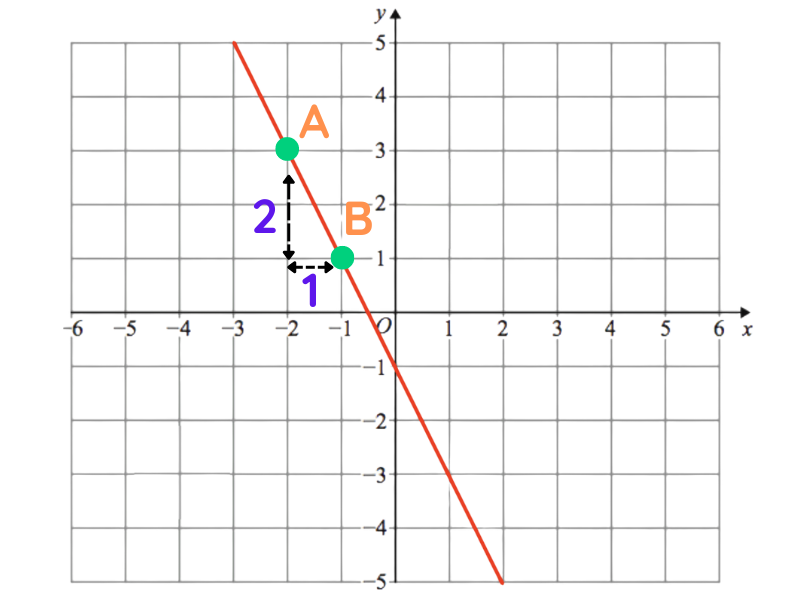
Step 2: Calculate the Slope (m)

  • Choose two clear points on the line where it crosses grid lines for accuracy.
  • For instance, point A at (x₁, y₁) and point B at (x₂, y₂).
  • Calculate the change in y: Δy = y₂ – y₁.
  • Calculate the change in x: Δx = x₂ – x₁.
  • Compute the slope: m = Δy / Δx.

Calculation:

  • From point A to point B, y decreases by 2 units (Δy = -2), and x increases by 1 unit (Δx = 1).
  • Therefore, m = -2 / 1 = -2.
  • Write the Equation: Substitute the slope and y-intercept into the slope-intercept form: y = m x + c.

A graph showing two points A and B with slope calculation where Δy = -2 and Δx = 1.

Using m = -2 and c = -1, the equation is y = -2 x – 1.

Point-Slope Form

The point-slope form is useful when you know the slope of a line and one point through which it passes.

Formula

The point-slope form is written as:

  • y – y₁ = m ( x – x₁ )

A graph illustrating the point-slope form of a linear equation, with the formula y - y₁ = m(x - x₁).

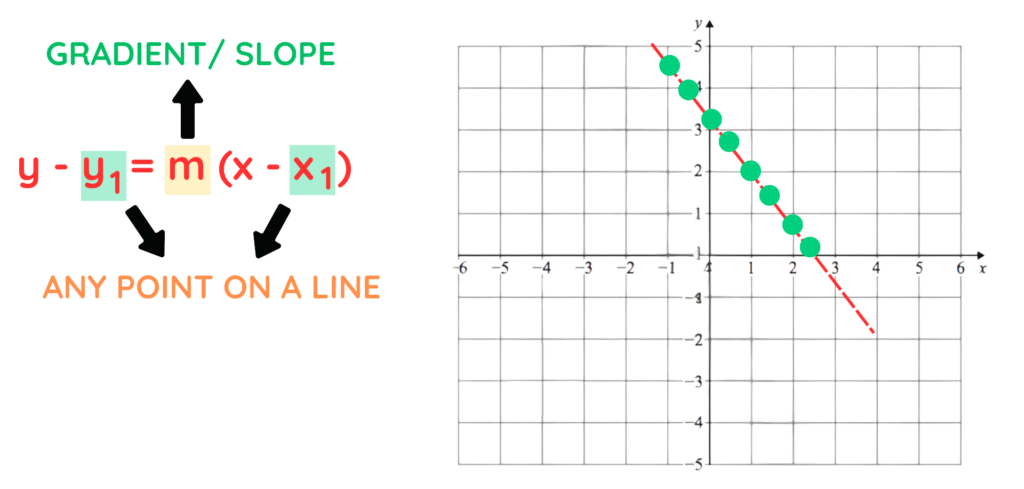
Where:

    • m is the slope or gradient of the line.
    • ( x₁, y₁ ) is the coordinated of a known point on the line

certified Physics and Maths tutor

 

 

Solved Example 3: Finding the Equation of a line with point-slope form

Question: A line has a gradient of -4/3 and it passes through the point (15,18).Find the equation of the line.

 

Solution: 

Given:

  • Slope (m): -4/3
  • Point: (15, 18)

Step 1: Substitute the given values into the formula:

y – 18 = (-4/3)(x – 15)

 

Step 2: Simplify the Equation:

  • To eliminate the fraction, multiply both sides by 3:

3(y – 18) = -4(x – 15)

  • Expand both sides:

3y – 54 = -4x + 60

Step 3: Rewriting into Slope-Intercept Form (Optional):

  • Rearrange the equation to solve for y: 

3y = -4x + 114

y = (-4/3)x + 38

Two-Point Form

The two-point form is ideal when you have two points on a line and need to find its equation.

Formula

The two-point form is written as:

  • ( y – y₁ )/( x – x₁ ) = ( y2 – y₁ )/( x2 – x₁ )

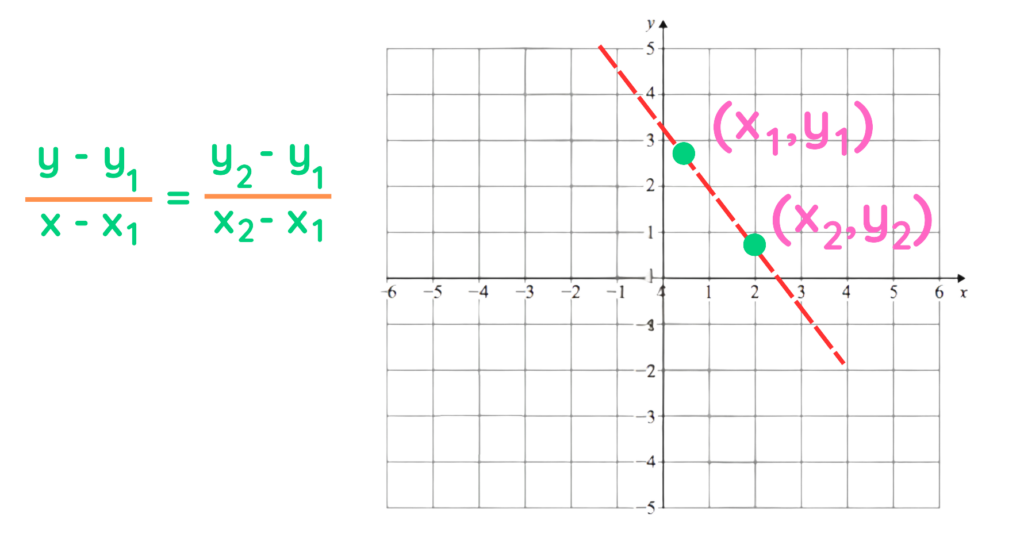
A graph illustrating the two-point form of a linear equation, with the formula (y - y₁)/(x - x₁) = (y₂ - y₁)/(x₂ - x₁).

Where:

    • ( x₁, y₁ ) and ( x₂, y₂ ) are two known points on the line

certified Physics and Maths tutor

 

 

Solved Example 4: Finding the Equation of a line with two-point form

Question: The point A (-3,5) and the point B (1,-15) lie on the line L. Find the equation of the line L.

Solution: 

Given:

  • Point A: (-3, 5)
  • Point B: (1, -15)

Step 1: Calculate the Slope (m):

m = ( y₂ – y₁ ) / ( x₂ – x₁ )

m = ( -15 – 5 ) / ( 1 – (-3) )

m = ( -20 ) / ( 4 ) = -5

Step 2: Use One Point in the Point-Slope Form:

  • Using point A (-3, 5):

y – 5 = -5 ( x – (-3) )

y – 5 = -5 ( x + 3 )

y – 5 = -5 x – 15

y = -5 x – 10

Interpretation: The equation y = -5 x – 10 represents the line passing through the points (-3, 5) and (1, -15).

Standard Form

The standard form presents the linear equation in a general way, often used for various algebraic manipulations.

Formula

The standard form is written as:

  • ax + by + c = 0

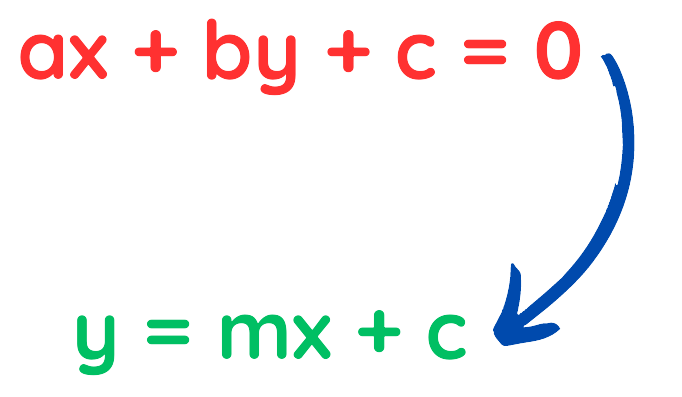
Conversion from the standard form of a linear equation (ax + by + c = 0) to the slope-intercept form (y = mx + c).

Where:

  • a, b, and c are constants.
  • x and y are variables.

certified Physics and Maths tutor

 

 

Solved Example 5: Converting to Slope-Intercept Form

Question: A line has equation 6x + 2y + 9 = 0

(a) Find the gradient of the line.

(b) Find where the line crosses the y-axis

Solution: 

Given:

  • Equation: 6 x + 2 y + 9 = 0

Step 1: Solve for y:

2 y = -6 x – 9

y = (-6 x – 9) / 2

  • Simplify:

y = -3 x – 4.5

Step 2: Identify the Slope and Y-Intercept:

  • Slope (m): -3
  • Y-intercept (c): -4.5

Interpretation:

  • The line has a slope of -3, indicating it falls steeply from left to right.
  • It crosses the y-axis at (0, -4.5).

Summary

Understanding these four forms allows you to tackle various problems involving straight lines.

1. Slope-Intercept Form (y = m x + c):

  • Quick identification of slope and y-intercept.
  • Ideal for graphing and analyzing linear relationships.

2. Point-Slope Form (y – y₁ = m ( x – x₁ )): 

  • Useful when you know one point and the slope.
  • Simplifies finding the equation of a line with limited information.

3. Two-Point Form (( y – y₁ ) / ( x – x₁ ) = ( y₂ – y₁ ) / ( x₂ – x₁ )):

  • Best when you have two points.
  • Calculates the slope and forms the equation simultaneously.

4. Standard Form (a x + b y + c = 0):

  • General representation.
  • Useful for solving systems of equations and certain algebraic manipulations.

Conclusion

Understanding and applying the four basic forms of straight-line equations is crucial in algebra and coordinate geometry. Each form serves a specific purpose, and knowing when to use each one simplifies solving linear equations and graphing lines.

  • Use the slope-intercept form when you need to quickly graph a line or identify its slope and y-intercept.
  • Use the point-slope form when you know a point on the line and its slope.
  • Use the two-point form when you have two points on the line.
  • Use the standard form for general purposes or when dealing with systems of equations.

Practice regularly with different types of problems to strengthen your understanding and proficiency in working with straight-line equations.

Practice Questions and Answers on Straight Line Equation

Question 1: Find the equation of the line that passes through the point (6, -2) and has a slope of 3.

Question 2: Given the points (0, 7) and (4, 15), find the equation of the line passing through them.

Question 3: Convert the standard form equation 5x + y – 10 = 0 into slope-intercept form and identify the slope and y-intercept.

Question 4:Find the equation of the line perpendicular to y = 1/2x – 3 and passing through the point (4, 1).

Question 5: Determine the equation of the line that passes through the points (-2, -5) and (3, 10).

Question 6: A line has a slope of 4 and a y-intercept of −7. Write its equation and convert it to standard form.

Question 7:Determine the equation of the line passing through the points (2, -3) and (-4, 9).

Question 8: Given the line 7y − 14x = 21, find its slope and y-intercept.

Question 9: Find the equation of a line with an undefined slope passing through the point (4, -2).

Question 10: Find the equation of a line with zero slope passing through the point (-3, 7).

Solutions

Question 1: 

Step 1: Use the Point-Slope Form:

y − y1​ = m (x − x1​)

y − (−2) = 3 (x − 6)

  • Simplify:

y + 2 = 3x − 18

Step 2: Simplify the Equation: Rearrange:

y = 3x − 20

Answer: The equation of the line is y = 3x − 20.

Question 2:

Step 1: Calculate the Slope (m):

m = ( y₂ – y₁ ) / ( x₂ – x₁ )

m = ( 15 – 7 ) / ( 4 – 0 )

m = ( 8 ) / ( 4 ) = 2

Step 2: Use the Point-Slope Form with (0, 7):

y − 7 = 2 (x − 0)

  • Simplify:

y − 7 = 2x

Step 3: Simplify the Equation:

y = 2x + 7

Answer: The equation of the line is y = 2x + 7

Question 3:

Step 1: Solve for y:

y = −5x + 10

Step 2: Identify the Slope and Y-Intercept:

  • Slope (m): − 5
  • Y-intercept (c): 10

Answer:

  • The slope-intercept form is y = −5x + 10
  • The slope is −5, and the y-intercept is 10.

Question 4:

Step 1: Find the Slope of the Given Line:

  • The slope of the given line is m1 = 1/2

Step 2: Find the Slope of the Perpendicular Line:

  • m2 ​ = −2 (negative reciprocal of 1/2)

Step 3: Use the Point-Slope Form with (4, 1):

y − 1 = −2 (x − 4)

  • Simplify:

y − 1 = −2x + 8

Step 4: Simplify the Equation:

y = −2x + 9

Answer:

  • The equation of the perpendicular line is y = −2x + 9

Question 5: 

Step 1: Calculate the Slope (m):

m = ( y₂ – y₁ ) / ( x₂ – x₁ )

m = ( 10 – (-5) ) / ( 3 – (-2) )

m = 15 / 5 = 3

Step 2: Use the Point-Slope Form with (-2, -5):

y − (−5) = 3 (x − (−2))

  • Simplify:

y + 5 = 3 (x + 2)

Step 3: Simplify the Equation:

y + 5 = 3x + 6

y = 3x + 1

Answer:

  • The equation of the line is y = 3x + 1

Question 6: 

Step 1: Write the Slope-Intercept Form:

4x − y = 7

Step 2: Convert to Standard Form:

  • Subtract 4x from both sides:

−4x + y = −7

  • Multiply both sides by −1:

4x − y = 7

Answer:

  • Slope-intercept form: y = 4x − 7
  • Standard form: 4x − y = 7

Question 7:

Step 1: Calculate the Slope (m):

m = ( 9 – (-3) ) / ( -4 – 2 )

= (12) / (-6) = -2

Step 2: Use the Point-Slope Form with one of the points:

  • Using (2, -3):

y – (-3) = -2 ( x – 2 )

  • Simplify:

y + 3 = -2 x + 4

Step 3: Simplify the Equation:

  • Rearrange to slope-intercept form:

y = -2 x + 1

Answer:

  • The equation of the line is y = -2 x + 1.

Question 8: 

Step 1: Convert to Slope-Intercept Form:

7y = 14x + 21

y = 2x + 3

Step 2: Identify the Slope and Y-Intercept:

  • Slope (m): 2
  • Y-intercept (c): 3

Answer:

  • The slope is 2, and the y-intercept is 3.

 

Question 9: 

Step 1: An undefined slope indicates a vertical line.

Step 2: Equation of a Vertical Line:

x = 4

Answer:

  • The equation of the line is x = 4

 

Question 10: 

Step 1: A zero slope indicates a horizontal line.

Step 2: Equation of a Horizontal Line:

y = 7

Answer:

  • The equation of the line is y = 7
Request for Demo Lesson

Table of Content